| 799、付过千般爱 在你手上 广义相对论40 |
| 送交者: 和颜清心 2019年08月04日02:39:36 于 [教育学术] 发送悄悄话 |
|
�� 3分钟 �
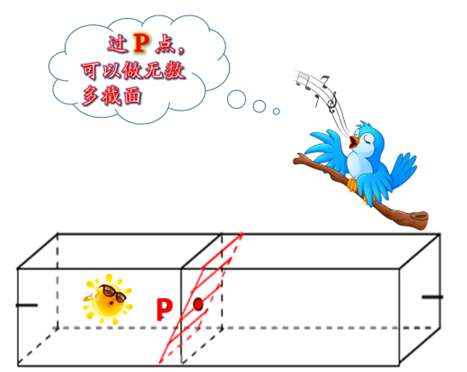
亲爱的朋友,根据常识,几乎人人皆知, 过某点可以作无数平面,
那么,是否要用无数平面上的应力, 才能描述某点的应力状况呢?回答是不需要。 物理上规定,只需用过一点的 ‘任意一组’相互垂直的三个平面上的应力, 就可以代表某一点的应力状态了。 而其它面的应力可以用与被考察面的方位关系来决定。 就是说,只要在无数可能产生的平面中 海选出一组做代表就可以了。
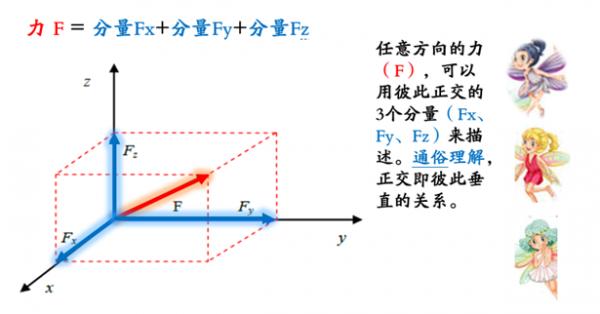
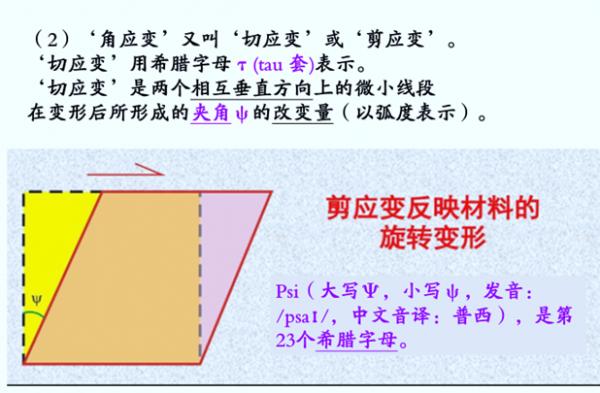
(图中的F 代表合力F) 应变有‘线应变’、有‘角应变’两大类。 (1)‘线应变’,又叫‘正应变’, (‘正应变’用一个长得像短尾巴小蝌蚪的 希腊字母Sigma 西格玛 σ来表示 ‘正应变’是在某一方向上的 微小线段因变形产生的长度增量与原长度的比值 ; (2)‘角应变’又叫‘切应变’或‘剪应变’。 ‘切应变’用希腊字母τ(tau 套)表示。 ‘切应变’是两个相互垂直方向上的微小线段 在变形后所形成的夹角的改变量(以弧度表示)。
从宏观角度说, 弹性是衡量物体抵抗弹性变形的能力, 从微观角度来说, 则是原子、离子或分子之间键合强度的反映。 想象在某个‘假想截面’的P点处, 切开物体,如下图所示。 根据定义,可以得到P点的 1 个‘正应力’和2个‘切应力’(剪应力)。 以上这3个分量(1个正应力、2个切应力)的合成, 叫‘全应力’, ‘全应力’用大写希腊字母 T (Tau) 表示。 我们可以用蟾蜍(英语Toad) 第一个字母T来帮助记忆。 通过学习,我们还知道 实际情况是,过某一点的受力,常常是复杂的, 那么如何能描述某一点的应力状态呢? 用向量显然不行, 物理上规定,在遇到具有多种方向的应力时, 需要使用‘具有多种方向’的物理量, 即使用一个叫‘张量’的东西来描述, 好像需要把‘粉条’换成‘洋葱头’。 粉条若是一维的; 洋葱头就是多维的(即葱头具有多重方向性)。 现在重点来了——
(3)什么是‘应力张量’( Stress tensor)?
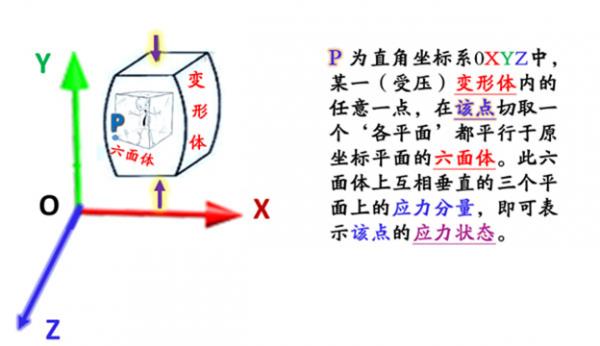
如图所示,P为直角坐标系0XYZ中, 某一(受压)变形体内的任意一点,
在该点附近
‘原坐标平面’的六面体(或叫单元体、微元体)。
此六面体上互相垂直的三个平面上的应力分量,
即可表示该点的应力状态 (实际上凡是‘正六面体’, 任意相邻的2个面,都是彼此垂直的)。
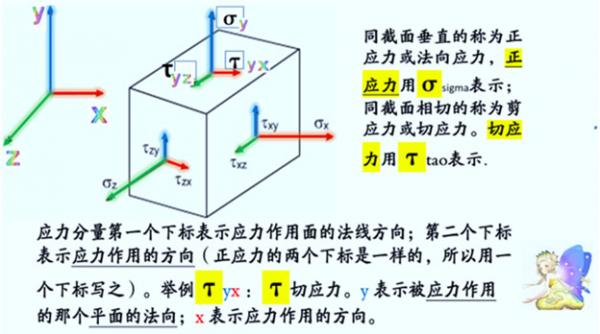
应力,即某点处单位面积上受到的力。
应力可分解为 “正应力”( 即 法向应力 )和切应力。
【单元体的概念】
何谓“单元”?我们可以将单元体定义为: 具有相同形状、体积或结构的 一个独立体或多个空间形体组合体, 由单元体生成整体。
一个应力分量,由 ‘截面方向’和 ‘分量方向’准确决定。 在数学上的表征就是, 某点的应力状态用一个‘二阶张量’来表示。 简单来说,应力张量是一个二阶物理量。 这种二阶状态可以理解为: 要把空间内某一点的所有面的方向说清楚, 需要三个‘面元方向’作基底, 在数学中,用很多小的平面描述一个曲面。 这些小的平面就叫“面元”,可理解为曲面上的小单元。
基 (basis)(即基底)是描述向量空间的基本概念。 向量空间‘基’的元素,称为基向量。 要把其中每一个‘面元方向’受力情况说清楚, 又各需要力的三个分量作基底, 如此一来,3乘3就得到9个分量。 【复习】
如图所示,P为‘直角坐标系’OXYZ中 一个(受压而变形的)‘变体’内的任意一点, 在‘该’P动手术, 切取一个各面都平行于 ‘原坐标面’的‘新六面体’, 这个新的‘六面体’,呱呱落地后,
自然会带来3个相互垂直的面, 但是在实际计算中, 根本不用取所有的面, 而只取1组3个相互垂直的面做代表, 这个作为代表的3个互相垂直的面上的‘应力量’, 即是该点的‘应力状态’ , 就是说,人们可以在这个‘六面体’上, 只取1组作为代表, 而这个‘代表组’所拥有的应力,就叫‘应力张量’。
【关于下标】 应力分量的 第一个下标表示作用平面的法向; 第二个下标表示应力作用的方向。 正应力的两个下标是一样的,故用一个下标简写之。 【小结】 场方程的“应力”, 是一个叫“应力张量”的二阶张量 (stress tensor 应力张量)。 概略地说,应力描述了物质内各部分之间通过力 (且是通过近距离接触的作用力) 进行相互作用的强度。 就是说, 相对论中,应力是二阶的,全称“应力张量” 。 三维空间中,某点需九个分量来确定这个张量 即三维空间的某一点需要用 3个‘正应力’和 6个‘剪应力’来确定。 |
|
|
|
|
 |
 |
| 实用资讯 | |
|
|
|
|
| 一周点击热帖 | 更多>> |
|
|
|
| 一周回复热帖 |
|
|
|
|
| 历史上的今天:回复热帖 |
| 2018: | 数学:应用和乐趣 (修订版) | |
| 2018: | 心脑一体化架构图——作为本博有关联性 | |
| 2017: | 彭运生谈艺录(87) | |
| 2017: | 中国餐桌上的文化与情感 | |
| 2016: | 第一部 东方的智慧 | |
| 2016: | 如来真义(四) | |
| 2015: | 鲁梦十四年春 | |
| 2014: | 中军:这样对郭美美公平吗 | |
| 2014: | D.QU: 中华最早童谣平仄格律及其声韵之 | |




 �
�
 )
)
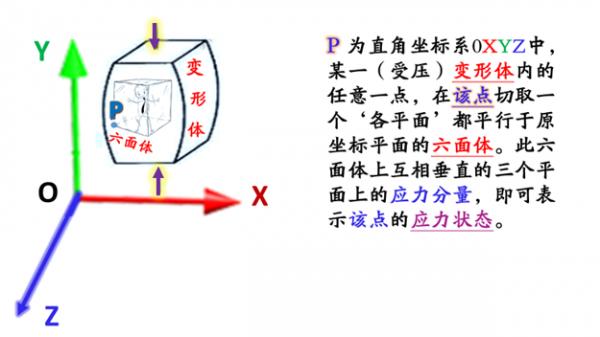
 切取一个‘各平面’都平行于
切取一个‘各平面’都平行于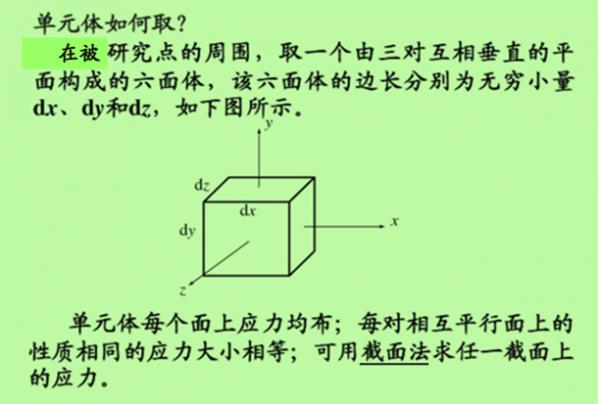
 谢谢。
谢谢。