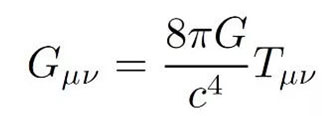| 801川普开金口,必有伏笔;要言引力场方程 广相论42 |
| 送交者: 和颜清心 2019年08月07日13:49:10 于 [教育学术] 发送悄悄话 |
|
29分
《引力场方程》 亲爱的朋友,
今天我们要对引力场方程作个总结:
引力场方程描述了时空的几何性质。
这是一个张量方程。
引力场方程的性质是属于‘非线性偏微分方程’。
场方程的“张量”,都有2个希腊字母来作下标,
如,Guv (爱因斯坦张量) 等。 这种带2个字母下标的张量,叫“二阶张量”。
μ 近似音读 缪/mju:/, ‘缪斯’的‘缪’;
ν 近似音读 妞 /nju/ 。‘妞’当女孩讲。
在古代,缪斯是主管艺术和科学的九位女神的总称。
G,也是Grace (优美)的第1个字母, 我们可以用‘Grace科学女神’来帮助记忆。
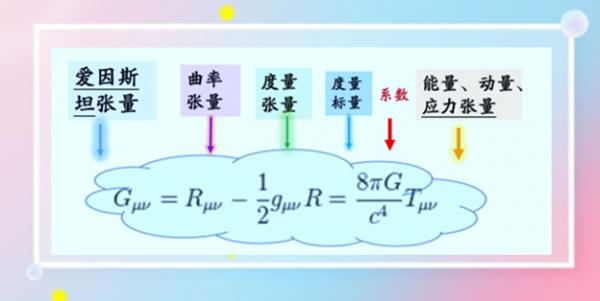
如上述,作为引力场符号的G μν ,学名叫
‘爱因斯坦张量’。引力:Gravitation ,头一个字母,是G。 爱因斯坦张量 G μ ν是个大概念。
大概念下又有 7 个小概念:
第1小概念:
“曲率张量” R (μ ν) :
“曲率张量”用来描述弯曲空间的曲率。
在微分几何中,它的学名叫“黎曼张量”
或叫“里奇张量”。
【曲率,即,弯曲程度。就是说,
弯曲空间偏离 平直空间 的程度,用曲率表示。】
“黎曼(里奇)张量”是说,
在某种逻辑推演中,
空间曲率的数学描述是可以得到简化或‘缩并’的。
注:缩并是一种有关简化的运算。
缩并,可以在某种逻辑推演中,将一种复杂的张量,
经过推演而等价于一种较为简单的张量。
第2小概念:
“ 里奇标量(R) ”: “ 里奇标量(R) ”代表纯量曲率, 它是从“里奇张量”简化形成的; 所谓标量(即数量)是不涉及方向的量。 “里奇标量 “R”也是一种曲率,
只不过这种空间曲率, 是在特殊条件下的空间曲率。
“ 度量张量 “度量张量 ”,也叫度规张量,
是用来衡量4维空间的距离和角度的。
在引力场方程中,
度量张量与里奇标量 乘积的二分之一 1/2 自然也是一种张量,
这个张量同样也可看作是 弯曲空间曲率的数学描述。
“能量-动量-应力张量 能量-张量-应力,也称 ‘能、动张量’,等。
“能-动-应力张量 ”
代表空间的能量密度和动量密度等。
这个张量也是二阶的。
第5个小概念: G(Gravitational constant)是“引力常数” ;
第6个小概念: C是真空中的光速。 第7个小概念 π是圆周率,是基本的几何常数之一。
好了,写到这儿里,
我们是否可以对场方程有些印象了。 综上所述,爱因斯坦场方程,
表述的是“空间弯曲”的情况。
数学上的空间弯曲,从何而来?
就是从‘爱因斯坦场方程’推演而来的。
已经得到天文观测的验证。
爱因斯坦场方程,是广义相对论的核心, 它使用数学语言精确地描述了 物质的性质与时空的联系。 场方程使用了黎曼几何中的概念和方法。 在黎曼几何中, 空间(或时空)的几何性质 被一个叫做'度规张量' 的概念所描述。 众所周知,简单的坐标 不能提供足够的信息, 来描述球面或更复杂空间的几何性质。 这些信息,只能由“度量张量”等来描述。 “度量张量”是定义在曲面空间中所有点的函数。 所有与几何相关的量, 比如曲线的长度、两条曲线相交的 角度等,都能通过“度量张量”计算出来。 我们知道,时空、物质等都是互相联系的。 爱因斯坦通过用一些较小概念(曲率张量等), 来推演另一个较大概念 G μν, 以这种方法来表示这些联系。 引力场方程可以简化成,如下形式:
爱因斯坦场方程的意义 这个方程 一边是几何量;一边是物理量 即, 左边是描写时空性质的几何量; 右边是描写物理性质的物理量。 就是说,爱因斯坦引力场方程
是用等号连结了‘空间结构’
和‘空间中物质、能量的分布’,
或者说,弯曲时空
等于空间中的物质、能量的分布 凭这个方程, 可以对时空和物质 是如何相互影响的在数学领域有了了解。
《有关‘应力分量’的正负值问题》 应力分量是能确定物体中
某一点应力状态的3个相互垂直面上的
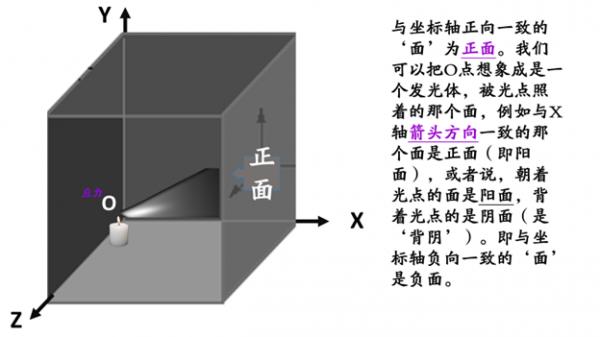
正应力和剪应力,共9个应力量。 为了计算应力分量, 首先要确定该应力 所在‘截面的(坐标轴的)方向’, 然后再确定‘应力作用的方向’。 具体的说,是要找出: ‘应力分量’的法向。法向即法线的方向。 习惯上,我们取三个正交截面的应力向量 (即x轴、y轴或z轴), 分别为三个截面各自的法向。 就是说, 为规定应力分量的正负号, 首先假设:法向 与坐标轴正向一致的面为正面; 与坐 标轴负向一致的面为负面。 进而规定: 正面上指向坐标轴正向的应力为正,反之为负; 负面上指向坐标轴负向的应力为正,反之为负。 三个正面上共有九个应力分量 (包括三个正应力和六个切应力)。
在标准空间直角坐标系里, 分别将X轴、Y轴或Z轴箭头所指方向,称为正向; 反之则是负向。
model of a perfect communion, help us to receive jesus worthily
完美的圣餐仪式,帮助我们接受耶稣的信仰。谢谢。 |
|
|
|
|
 |
 |
| 实用资讯 | |
|
|
|
|
| 一周点击热帖 | 更多>> |
|
|
|
| 一周回复热帖 |
|
|
|
|
| 历史上的今天:回复热帖 |
| 2018: | 昨天我发布的打印论文被宰之事。美国白 | |
| 2018: | 《两片嫩叶》 | |
| 2017: | 关于量子保密通讯 | |
| 2017: | 2018美国留学费用表 | |
| 2016: | 和颜清心:思想的形成 人问寒山路 | |
| 2016: | 思想的形成 不是风动、不是幡动,仁者 | |
| 2015: | 是骡子是马拉出来遛遛-你真的英语好吗 | |
| 2015: | 令人嘘唏不已的耶鲁大学原址 | |
| 2014: | 老几:胡适对孔子思想的误解 | |
| 2014: | 范例的微观世界与宏观世界的关系 | |