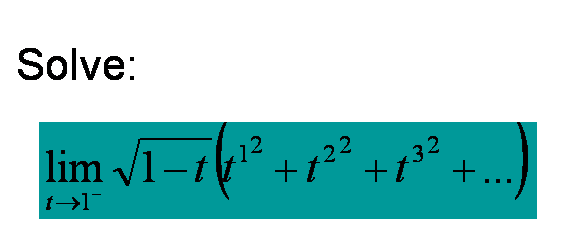| 一年级极限数学题比较细腻的解答(改错重贴) |
| 送交者: 粱远声 2016年01月03日08:25:37 于 [灵机一动] 发送悄悄话 |
|
一年级极限数学题讨论解稍嫌粗糙
我曾这样解过这道题:
根据不等式 1 - x < e^(-x), 很容易证明 (1 - dx^2)^(k^2) < e^(-(kdx)^2) 要想证明 e^(-((k+1)dx)^2) < (1 - dx^2)^(k^2), 只需证明 e^(-((1+1/k)dx)^2) < 1 - dx^2 (1) 令 y = 1 - x^2 - e^(-(1+1/k)^2 x^2) y(0) = 0 dy/dx = 2x((1+1/k)^2 e^(-(1+1/k)^2 x^2) - 1) 如果找到x的区间使得dy/dx > 0。 这个区间也是(1)成立的区间。问题归结为,找到x的区间使得
e^(-(1+1/k)^2 x^2) < (1+1/k)^2
令 x = d/n。 问题归结为,找到d的区间使得 e^(-(1+1/k)^2 (d/n)^2) < (1+1/k)^2 d^2 < (2n^2/k)ln(1+1/k)^k/(1+1/k)^2 因为ln(1+1/k)^k单调增加,(1+1/k)^2单调减少, Min ln(1+1/k)^k/(1+1/k)^2 = ln(2)/4 当 d^2 < 2nln(2)/4 时, (1)成立。 取 d = sqrt(n)/2; dx = d/n; lim(n->inf)dx = 0; lim(n->inf)d = inf, 我们有 e^(-((k+1)dx)^2) < (1 - dx^2)^(k^2) < e^(-(kdx)^2) 令 f(n) = ( (1 - dx^2)^(1^2) + (1 - dx^2)^(2^2) + ... + (1 - dx^2)^(n^2))dx p(n) = (e^( -dx^2) + e^(-(2dx)^2) + ... + e^(-(ndx)^2))dx g(n) = (e^( -2dx^2) + e^(-(2dx)^2) + ... + e^(-((n+1)dx)^2))dx 得到 g(n) < f(n) < p(n) 因p(n), g(n)趋近于同一极限Int(0,inf)[e^(-x^2)dx] 所以 f(n) 趋近于 Int(0,inf)[e^(-x^2)dx] |
|
|
|
|
 |
 |
| 实用资讯 | |
|
|
|
|
| 一周点击热帖 | 更多>> |
|
|
|
| 一周回复热帖 |
|
|
|
|
| 历史上的今天:回复热帖 |
| 2014: | 称12个小球的修改版 | |
| 2013: | 范儿98——美人计(中共):恒心与自律 | |
| 2011: | Eat in and Take out 有谁比我译得还好 | |