有地平主义者问，工程师在设计长桥时，是怎样考虑地“球”表面弧度问题的，认为如地球是个球的话，设计象中国胶州湾大桥那样长的桥，地表曲率应该无法忽略。（见这链接：国内的正好。不是中国造了世上最长的跨海大桥了吗，）。我跟贴讲，一般情况下地球弧度可以忽略。有地平主义者不服，开始信口开河胡扯起来。见下面截图。(链接在此：别和傻子扯了。）

那么24英里长的距离，地球弧线与直线间究竟有多大区别呢？此地平主义者说很简单的计算，可就是很简单的计算，他也懒得算。那么我在此就来帮他计算一下。

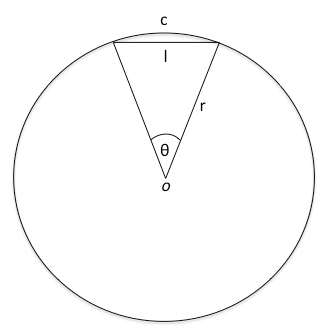
根据地球主义的理论，地球半径r=6378公里。下图为经过球心的地球截面示意图。图中c代表相对于直线l的弧线，r为地球半径，θ为c的跨度，。24英里约等于38公里。那么如c=38公里，l=?

θ= 2πc/(2rπ) = c/r = 38/6378 = 0.0059579805

l = sin(θ/2)2r = sin(0.0059579805/2)*2*6378 = 37.9999415892

38 - 37.9999415892 = 0.0000584108公里 ＝ 0.0584米 ＝ 6 厘米

38公里长的桥，这几厘米的误差不可以忽略么？（如以l=38公里来计算c，这可以作为给夭夭的附加题。）地平主义者的论点基本都是信口开河讲的。如还有如地球是个球，那在飞机上看地平线应该看到弧度的论点，也完全只是凭空想象。对这我也作了计算，证明了在一般民航客机上看地平线，是难以觉察到地平线的弧度的。（见链接：在高空客机上能感觉到地球地平线的弧度么？）

很搞笑的是，地平主义者为了证明地球是平的，竟然还用基于地球是个球的原理制造的仪器来测量距离。