先看視頻。 有人認為這是惡作劇,但也可能是車主想做個物理實驗,但不會計算,結果悲劇了。
所以,理論還是有用啊。力學這東西,還在300多年前被牛頓一個 f=ma 全部搞定。大家要記住,凡是涉及機械運動的事情,都是可以用 f=ma 算的。懂力學的,不跟你瞎掰,裝,而是實打實,算。即使沒有解析解,也得數值計算。這道題,我推薦作為高考題。

設汽車啟動後迅速達到勻速運動狀態。已知汽車牽引處高度為h, 繩子長度為L,重力加速度為 g, 忽略石頭、地面摩擦力(也就不考慮石頭開始被卡住的情況),假定繩子為理想繩(無機械能損耗)。
問: 石頭會不會砸到車?
有興趣的自己先解答下。我後面的答案只做參考。

解答:設繩子拉到最長時與地面夾角為 θ
根據題中的已知 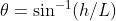 。
。
解答這個題顯然以勻速運動的汽車為參照最為方便,否則還得考慮車也在動。這個參照的選擇不改變動力學,不是源自牛頓,而是更早的伽利略。學科學知道些歷史有好處。
顯然,以車為參照,石頭飛起速度
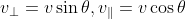
(為什麼??? 式子寫出來,大家思考,想明白了,剩下的就容易了,模擬高考就能上二本了)。
水平分量
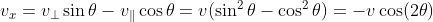
垂直分量
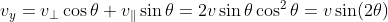
可見,石頭是以速度 v (相對車來說), 是以二倍的角度飛過去。得到這個結果,我開始感到有趣。從視頻看,石頭確實是以大於繩子角度的角度“追擊”汽車。再想想,其實這相當於彈性反射嘛 -- 反射角等於入射角。繩子是入射 法線。如果一開始就想到這個,都不需要算了。
剩下的事情簡單了,我們只需要計算石頭相對於車的飛行距離。
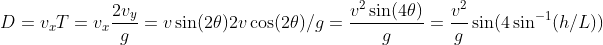
可見,繩子與地面角度為 90/4 = 22.5 度石頭飛得最遠。
石頭砸到車子需要  。慢慢解。
。慢慢解。
但我們可以粗略看看,如果車速十米/秒,那麼石頭最大追擊距離也在幾米的量級,要躲過石頭繩子不能太短。當然,慢慢開也好。











