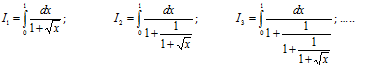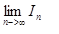| 积分智力题试解 (修改) |
| 送交者: 粱远声 2017年08月11日16:35:12 于 [灵机一动] 发送悄悄话 |
|
定义:
求
积分智力题试解 先讨论被积函数的分母。f1(x) = 1 + x^0.5, f2(x) = 1 + 1/f1(x), f3(x) = 1 + 1/f2(x), fn+1(x) = 1 + 1/fn(x) fn(x) > 1 fn+1(x) - fn-1(x) = 1 + 1/(1+1/fn-1(x)) - fn-1(x) = (1 - fn-1(x) - fn-1^2(x))/(fn-1(x) + 1) < 0 这样我们得到 fn+1(x) < fn-1(x) (1) fn(x) > 1 (2) (1) 说明x在(0,1) 区间奇数列单调减少,偶数列单调减少。(2)说明数列有下界。所以奇数列收敛,偶数列收敛。接下来看看数列的极限是什么。在(0,1) 区间任取x0, 假设奇数列收敛于a, 根据递推公式 fn+1(x0) = 1 + 1/(1+1/fn-1(x0)) (3) 得到 a = 1 + 1/(1+1/a) (4) 解得 a = (1+5^0.5)/2 (5) (3)也是偶数列的递推公式,所以(5) 也是偶数列的极限值。奇偶列收敛于同一个极限,推出 fn(x0) 收敛。由于x0的任意性,fn(x) 收敛于常数 a。 所以 In 收敛于 1/a |
|
|
 | |
|
 |
| 实用资讯 | |