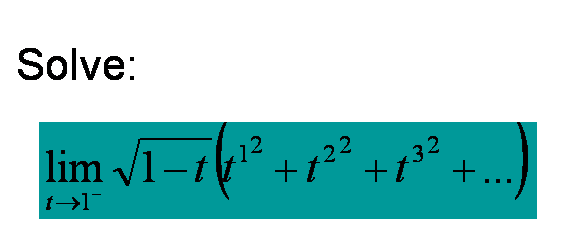| 一年级极限数学题讨论 |
| 送交者: 粱远声 2012年11月05日17:18:05 于 [灵机一动] 发送悄悄话 |
|
求: lim(t->1-) sqrt(1-t)(t^(1^2) + t^(2^2) + t^(3^2) + ... + t^(n^2) + ...) 令 dx = sqrt(1-t) t = 1 - dx^2 sqrt(1-t)(t^(1^2) + t^(2^2) + t^(3^2) + ... + t^(n^2) + ...) = dx( (1 - dx^2)^(1^2) + (1 - dx^2)^(2^2) + (1 - dx^2)^(3^2) + ... + (1 - dx^2)^(n^2) + ...) = dx( [(1 - dx^2)^ (1/dx^2)]^(dx^2)] + [(1 - dx^2)^(1/dx^2)]^((2dx)^2) + [(1 - dx^2)^(1/dx^2)]^((3x)^2) + ... + [(1 - dx^2)^(1/dx^2)]^((nx)^2) + ... ) 因为[(1 - dx^2)^(1/dx^2)] -> e^(-1) 上式可近似写成 上式 = (e^( -dx^2) + e^(-(2dx)^2) + e^(-(3dx)^2) + e^(-(ndx)^2) + ...)dx 让dx趋近于0, 上式 -> Int(0,inf)[e^(-x^2)dx] 令 c = Int(0,inf)[e^(-x^2)dx] c^2 = lim(b->inf) Int(0, b)[Int(0,b)[exp(-(x^2+y^2))dy]dx] 令 r^2 = x^2+y^2 dxdy = rdrda c^2 = lim(b->inf) Int(0, pi/2)[Int(0,b)[exp(-r^2)rdr]da] = lim(b->inf) (pi/2)(-1/2)Int(0,b)[exp(-r^2)d(-r^2)] = pi/4 c = sqrt(pi/4) |
|
 |
 |
| 实用资讯 | |
|
|
| 一周点击热帖 | 更多>> |
| 一周回复热帖 |
| 历史上的今天:回复热帖 |
| 2011: | 唐奕vs吉田美香:高手对局中的疑问手 | |
| 2009: | 从1到100,其中拿掉1或者2个数字,给个 | |
| 2009: | 两数字分别赋予两个变量,要求在不增加 | |