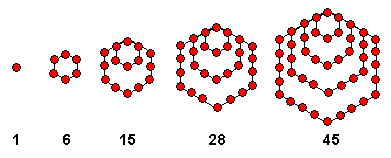| 【數學】幾個2階等差數列 |
| 送交者: gugeren 2017年05月27日11:44:57 於 [教育學術] 發送悄悄話 |
|
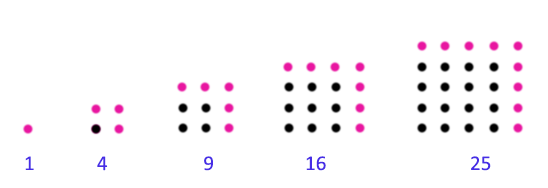
【數學】幾個2階等差數列 人們對等差數列(又名“算術數列”)非常熟悉。 1,2,3,...,n,...,是公差為1的等差數列,n>=1。 2,4,6,...,2n,...,是公差為2的等差數列,n>=1。 1,4,7,...,n+3,...,是公差為3的等差數列,n>=1。 這裡的3個帶有n的表達式,稱為等差數列的(普)通項。 現在看看另一種數列。 以下4個數列的各項數字,分別整齊地排列起來,可以各自構成一個多面體,故它們也統稱為“多面體數(polygonal number)”。 1] 三角形數(triangular number):其通項T(n)= 1/2 n^2 + 1/2 n(其前5項為1, 3, 6, 10, 15)。 【有關“三角形數”的詳情,請看本博博文《有趣的三角形數》。】 2] 平方數/正方形數(square number):其通項S(n)= n^2(其前5項為1, 4, 9, 16, 25)。 【圖1:平方數】
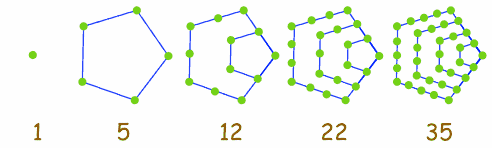
3] 五邊形數(pentagonal number):其通項P(n)= (3/2)*n^2 - 1/2*n(其前5項為1, 5, 12, 22, 35)。 【圖2:五邊形數】
4] 六邊形數(hexagonal number):其通項H(n)= 2*n^2 - n(其前5項為1, 6, 15, 28, 45)。 【圖3:六邊形數】
這些數列相鄰兩項之間的差,稱為“級差”。 根據上述4個數列,可以看出,它們的4個級差分別是: 1] 三角形數(triangular number):當n>=2時,其第n項與第(n-1)項間的級差為 n,它們分別是2, 3, 4, 5, ...。 2] 平方數/正方形數(square number):當n>=2時,其第n項與第(n-1)項間的級差為 2n-1,它們分別是3, 5, 7, 9, ...。 3] 五邊形數(pentagonal number):當n>=2時,其第n項與第(n-1)項間的級差為3n-2,它們分別是4, 7, 10, 13, ...。 4] 六邊形數(hexagonal number):當n>=2時,其第n項與第(n-1)項間的級差為4n-3,它們分別是5, 9, 13, 17, ...。 容易看出,這些數列兩項之間的級差的級差分別是相同的: 數列1] 的兩項之間的級差的級差是1。 數列2] 的兩項之間的級差的級差是2。 數列3] 的兩項之間的級差的級差是3。 數列4] 的兩項之間的級差的級差是4。 這就是“2階等差數列”的定義:由一個數列的級差形成的新的等差數列。這些新數列的通項公式就是原數列的級差。 因此,可以把一般意義上的等差數列看作為為1階的等差數列。 也可以由此定義更高階的等差數列,如3階等差數列、4階等差數列,……。它們通稱“高階等差數列”。 縱觀中國數學史,中國的兩宋的數學家沈括(1031-1095)和楊輝(約1238-約1298年),元代數學家朱世傑(1249-1314),以及清代數學家李善蘭(1810-1882)等幾代數學家,都對高階等差數列做出了貢獻。 欲求各個數列的前k項之和,可先從求數列2]的連續自然數的平方和的前k項入手。這4種數列通項的最高次都僅是2次方,故計算起來不難。 1] 三角形數(triangular number):其前k項之和S(3,k) = n(n+1)(n+2)/6 2] 平方數/正方形數(square number):其前k項之和S(4,k) = n(n+1)(2n+1)/6 3] 五邊形數(pentagonal number):其前k項之和S(5,k) = n^2*(n+1)/2 4] 六邊形數(hexagonal number):其前k項之和S(6,k) = n(n+1)(4n-1)/6 == 相關鏈接和書籍: Square number: https://en.wikipedia.org/wiki/Square_number Pentagonal number: https://en.wikipedia.org/wiki/Pentagonal_number Hexagonal number: https://en.wikipedia.org/wiki/Hexagonal_number 垛積術(即“高階等差數列”): https://zh.wikipedia.org/wiki/%E5%9E%9B%E7%A7%AF%E6%9C%AF 李善蘭: https://zh.wikipedia.org/wiki/%E6%9D%8E%E5%96%84%E5%85%B0 李善蘭著作《垛積比類》: http://baike.baidu.com/item/%E5%9E%9B%E7%A7%AF%E6%AF%94%E7%B1%BB 朱世傑: https://zh.wikipedia.org/wiki/%E6%9C%B1%E4%B8%96%E6%9D%B0 吳文俊主編:中國數學史大系(10卷) |
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2016: | 粱遠聲:悖論是不存在的 - 解析之諾悖 | |
| 2016: | 安博:文王演八卦 難在一中 | |
| 2015: | 寫給父母:當孩子面臨傷痛 | |
| 2013: | 我的新表達-談條件結論 | |
| 2013: | 在美國教歷史不用擔心“不愛國”帽子 | |
| 2012: | 一滴水:參加女兒的哈佛畢業典禮(組圖 | |
| 2012: | 上海人真的很不夠意思。丫的當事的比見 | |