• 十二色定理

   

十二色定理 - 起源又叫Heawood定理。是一種有7個洞的曲面上構造兩兩相連的12個區域的極限。在人類在企圖證明四色定理過程中，發現了在曲面上作圖，反而更加容易。參見：八色定理，九色定理，十色定理，十一色定理，七色定理。

十二色定理

曲面染色結構定理

• 提出者

• 德國人林格美國楊斯等證明

• 證明時間

• 1974年

• 適用領域

• 交通樞紐-電路樞紐-芯片

• 
  

1. 1 定義

2. 2 歷史

3. 3 推導過程

4. 4 應用

5. 5 影響及意義

定義

 播報

十二色定理 - 起源又叫Heawood定理。人類在企圖證明四色定理過程中，發現了在曲面上作圖，反而更加容易。

證明四色定理過程聯想到曲面染色的問題。

公式來源

1974年德國的林格和美國的楊斯證明了：

證明這個公式，數學家用了78年。P是指這個曲面的洞的個數，又叫虧格。當虧格為7時：

方括號表示取整數。

如果p=7,則是

 即7個洞（又叫虧格7.）需要12個區域才能形成兩兩相連的形式。每一個區域與其他11個區域相連。

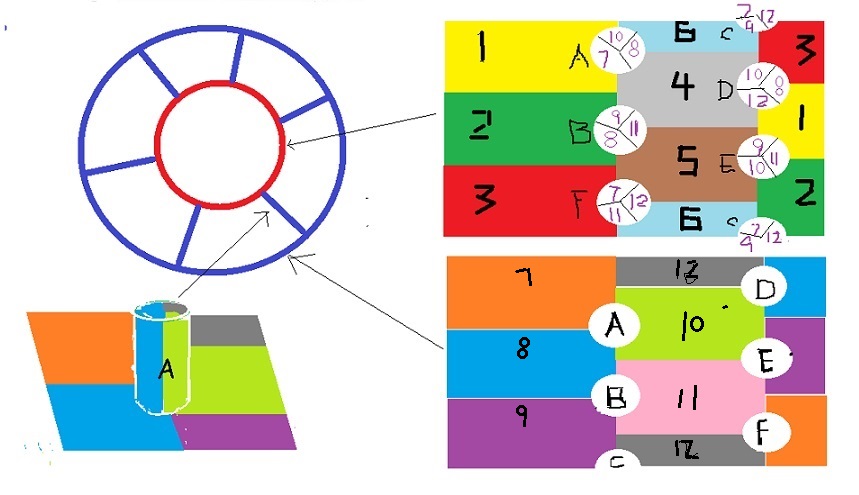
圖1，右上面是內環的平面圖。右下是外環平面圖，大於內環。片面圖上下對摺再左右對摺就是一個輪胎形狀。兩個輪胎一內一外，外環的ABCDEF有六個延伸的立柱，與內環對應，形成有12個區域兩兩相連。

公式和公式的證明來自：

《圖論導引》214頁，機械工業出版社。

王曉明設計並且製造實物體， . 並且給出了這個需要12種顏色染色的圖形：

圖2，實物圖證面

實物圖；

圖2圖3是實物全景圖，

表明：在有7個洞的曲面上染色成為兩兩相連的區域，11種顏色是不夠的。

歷史

 播報

數學家在研究四色定理時已經開始考慮曲面染色了，就是說有一百多年歷史了，1896年開始推理，1974年完成證明。王曉明設計圖形用了3年，製造實物用了2年。

推導過程

 播報

1974年德國的林格和美國的楊斯證明了上面的公式。

應用

 播報

廣泛應用於線路交叉，例如，管道樞紐，電路樞紐（芯片）。可以形成不會堵塞的交通。

影響及意義

論文發表以後，西方工程師已經在考慮應用於芯片設計。 [1] 

• 參考資料