| 淺談量子計算機-8 |
| 送交者: 天蓉 2024年02月20日15:02:11 於 [教育學術] 發送悄悄話 |
5.3 量子糾錯計算機和通信的基礎是比特,比特是物理系統產生的物理量,有時難免會出錯而影響所傳遞信息的可靠性。不過,發展成熟的經典計算技術,已經具有自動糾錯的功能,而如今正在起步的量子計算,也將糾錯提到議事日程上,並作為其成敗的關鍵因素。那麼,計算機到底是如何糾錯的?量子糾錯比較經典而言,又有哪些特別之處,如何克服?本文探討一下這些問題。
5.3.1,經典糾錯由來已久
提高系統的可靠性一般有兩種辦法:一是對硬件縝密設計和質量控制,儘量減少出錯的概率;二是以冗餘為代價來換取可靠性,算是軟件方面的努力。硬件的控制是有限的,必須利用軟件編碼來“容許”錯誤。因此我們主要介紹利用冗餘的容錯糾錯技術。
在計算和通訊中出現錯誤是很自然的事。上世紀五十年代的早期經典計算機,用電子管或繼電器構建的比特,會毫無預兆地發生反轉。為此數學家馮·諾伊曼提出利用冗餘比特來糾錯的容錯技術。冗餘糾錯很容易理解,比如說你電話中告訴別人你的名字,說一次不夠就說3次“我是張三、張三、張三……”,次數越多,傳錯聽錯的概率就越小。冗餘糾錯的方法便類似於此,最早的冗餘糾錯是奇偶校驗法【15】。
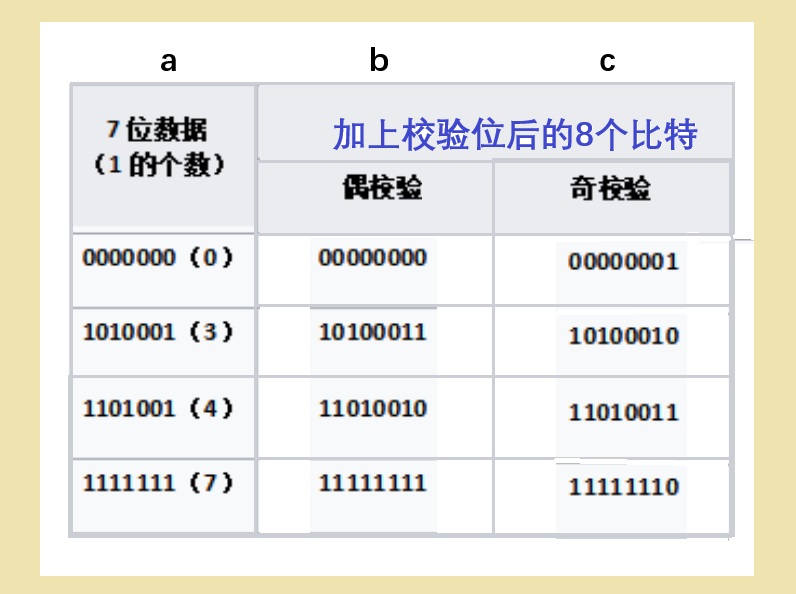
舉一個最簡單的奇偶校驗例子。如果我們需要傳遞7位數字的二進制數,也就是7個比特位。這一串7個比特值中有1有0,均有可能出錯。我們考慮7個比特位中1的個數n:因為傳遞的信息的隨機性,n也許是偶數也許是奇數,見圖1a。然後,我們在7個信息比特後面加一個比特,即加一個冗餘的比特,或稱校驗比特。校驗比特是設置為1還是0呢?由如下規律決定:如果原始信息比特中n是奇數,將校驗比特設置為1;如果原始信息比特中n是偶數,將校驗比特設置為0。也就是說,信息比特加上校驗比特共8個比特中,1的總數總是為偶數,見圖1b。
圖1:奇偶驗證例子
這樣的話,接收方收到8個比特後,如果其中1的總數是奇數,那就一定是出錯了!當然,這種方法並不能判定是哪兒出了錯,也無法糾正錯誤,但至少可以扔掉錯誤信息,讓對方重發一次。以上例子說的是奇偶校驗中的“偶校驗”,也可以類似地將校驗比特設置為“奇校驗”規則,如圖1c所示。
由於奇偶校驗很簡單,所以至今也還被使用。上例中的7個比特,只使用了一個校驗比特,就已經能檢查某些基本錯誤,如果再增加冗餘比特數,便可達到更準確有效的糾錯方法。還要說明的一點是:上述例子中所謂的“奇偶”,剛好與通常理解的“奇數偶數”概念相符合,但實際上,計算科學中的奇偶校驗,檢查的是parity,與檢查奇數偶數有所區別,比如下面的3比特糾錯。
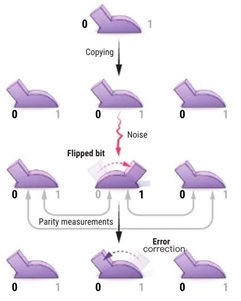
例如,可以對每個比特都做3份拷貝,為什麼是3呢?因為2份不是很合適,只有兩份的話,如果檢查到兩個數字不一樣,那是誰錯了呢?好像有點扯不清楚。3個就可以“服從多數”了。比如說,如果檢查錯誤時發現:第1個和第3個比特相同,但第1個和第2個、第2個和第3個都不同,那麼最有可能是第2個比特翻轉了,如圖2所示。於是計算機就把那個錯誤的比特再翻回來。冗餘數目越多,機器便具有越大的糾錯能力。不過,集成電路普及後,晶體管比特出錯幾率較小,糾錯技術在經典計算機中使用不是很多,但對它的研究還是比較深入的,容錯控制技術仍然經常被使用,特別是用於環境複雜、出錯因素比較多的通訊技術中。
圖2:3個重複比特的糾錯方法
不同應用場合的糾錯能力,可用不同的方法和指標來評估。例如,在數字通訊傳輸中有如下幾個定義:比特差錯數(bit errors),是接收到的數據流由於噪聲錯誤而更改的比特數; 比特錯誤率(bit error rate,BER)是指單位時間內錯誤的比特數; 比特誤碼率(bit error ratio,BER)是一段時間內錯誤比特數除以傳輸總比特數。 比特誤碼概率(bit error probability)是比特誤碼率的統計期望值。
因此,一般而言,數字通訊傳輸中的糾錯能力,可用比特誤碼概率(平均誤碼率)來評估,這個值越低,表明系統的糾錯能力越強。不同應用對誤碼率的要求不同,例如,語音和數據業務的典型所需BER性能分別為10−3 和 10−6。一般通訊信道要求誤碼率小於10-6。
5.3.2,量子糾錯3點困難
量子計算機有運算速度快的潛力,但量子比特卻十分脆弱,與周圍環境發生哪怕極微弱的相互作用也會導致它們發生改變,物理上被稱為“退相干”的效應。所以,量子糾錯是很重要的課題。 量子糾錯可以採用“利用冗餘”這個相同的理念,但在具體實施時,量子比特的困難很多【16】,有別於經典糾錯之處可以主要歸結為如下3點。
第一點是來自於量子比特與經典比特本質上的不同。量子誤差比經典比特誤差複雜得多。經典比特只有0、1兩種狀態,而量子比特是兩種狀態組成的所有疊加態。這相當於除了需要判斷0值或1值的變化之外,還需判斷態矢量在三維Bloch球面上的相位誤差,這是一個可以從0°到360°之間變化的連續變量,不是像(0、1)那種更易於判斷正確錯誤的離散量。 傳統計算機進行一個比特的冗餘糾錯,需要將它複製到其他比特上,然後對所有的比特進行測量以比較它們的數字規律來判定是否出現了錯誤。然而,量子力學原理使得直接通過複製並測量量子比特並檢測錯誤的方法完全不可行。因為量子力學中有一個不可克隆原理,即不可能構造一個能夠完全複製任意量子比特,而不對原始量子位產生干擾的系統。這是量子糾錯的第二個困難。
最後,糾錯的第3個困難是量子系統沒法“測量”。任何測量都將導致系統的波函數塌縮(或稱為退相干效應)。
基於上述困難,量子糾錯的發展過程中,甚至出現越糾越錯的情況。不過,科學家們在多年的研究和探索中,也找到一些辦法來克服量子糾錯的困難。總結起來一句話仍然是“增加冗餘的量子比特數”。即用多個物理量子比特,對應1個邏輯量子比特。所以,我們在判定量子計算機的能力時,不能僅僅看它的量子比特數,要看它的“邏輯量子比特數”。
5.3.3,如何克服量子困難
首先說說從原則上如何克服上述量子糾錯的3點困難。
第一點困難是由於量子疊加態的連續變換,使得早期時,人們認為這是製造可⽤量⼦計算機的根本障礙。人們認為,少數量⼦位執⾏的⼀些操作,難以擴展到具有許多量⼦位陣列、可以⻓時間運⾏的計算系統中。
後來,科學家們將量子比特的錯誤,歸於兩類錯誤:X錯誤和Z錯誤,X錯誤指的是量子位0、1的錯誤,與經典情況“位翻轉”的錯誤一樣,見圖3。然而,另一類Z錯誤是經典計算中沒有的,可以看作是布洛赫球面上相位的錯誤。量子比特的相位是連續變化的,但在量子糾錯時,相位的錯誤被量子化成了“相位翻轉”的離散值,用Z錯誤來表徵。因為量子糾錯多了一個Z錯誤,簡單的經典三量⼦位重複碼不能夠防⽌所有可能出現的量⼦錯誤。真正的量⼦糾錯需要更多的東⻄。20世紀90年代中期,AT&T⻉爾實驗室的彼得•秀爾(Peter Shor)描述了⼀種精美的⽅案,把3位重複碼嵌入另⼀個碼。也就是說,將⼀個邏輯量⼦位,用9個物理量⼦位進行編碼。秀爾的⽅案可以防⽌並糾正任何⼀個物理量⼦位上發⽣的任意量⼦錯誤。值得一提的是,這位提出量子糾錯的第一人,MIT 的數學教授秀爾,也是提出質因數分解量子算法的人。
秀爾也提出了辦法來克服量子態退相干不可測量的問題,以及量子比特不可克隆的困難,基本思想就是利用量子糾纏,這一個量子世界的獨特現象。秀爾讓編碼⼀個邏輯量⼦位的9個物理量⼦位互相糾纏在一起。有關量子糾纏這方面我們不予詳細介紹,有興趣者可參考相關文獻【3】。
圖3:經典糾錯和量子糾錯
那麼怎樣具體進行量子糾錯呢?再次回想一下經典糾錯,比如說:用“000”和“111”來代表“0”和“1”的方案,如果“000”中有一個比特發生了翻轉,我們通過讀出這三個比特發現錯誤,就可以糾正它。當然也有可能兩個比特同時發生錯誤,這時糾錯則將導致最終的錯誤。這樣的話,會不會“越糾越錯”呢?經典糾錯不會,因為根據概率規則,兩個錯誤同時發生的概率是發生一個錯誤概率的平方,而經典計算出錯概率很小,例如假設是萬分之一,那麼這個小概率的平方只有億分之一,更多的重複編碼,可以把錯誤率逐步降低倒幾乎為0,這就是經典糾錯的基本機制。
量子糾錯遵循同樣的思想。比特位發生翻轉的錯誤,被定義為X錯誤,符號(相位)發生翻轉的錯誤被定義為Z錯誤,這兩種錯誤也有可能同時發生,這時將其定義為XZ錯誤。三類錯誤(X、Z 、XZ),分別對應於量子力學中的泡利矩陣 X、Z 和 Y。糾正X錯誤的情況與經典情況一樣(圖3);為了糾正Z錯誤,可以用“000”和“111”的疊加態“+++”和“---”來編碼。如此,一共9個物理量子位,巧妙地組成某種嵌套式的編碼,就可以同時糾正X和Z的錯誤。這個用9個量子比特來代表一個邏輯量子比特,就是當年秀爾提出的第一個量子糾錯碼。如此構成的一個邏輯量子比特,其性能表現比一個物理比特更好。但是,因為量子系統的錯誤率太高了,糾錯本身也會發生錯誤,所以仍然有“越糾越錯”的可能性。
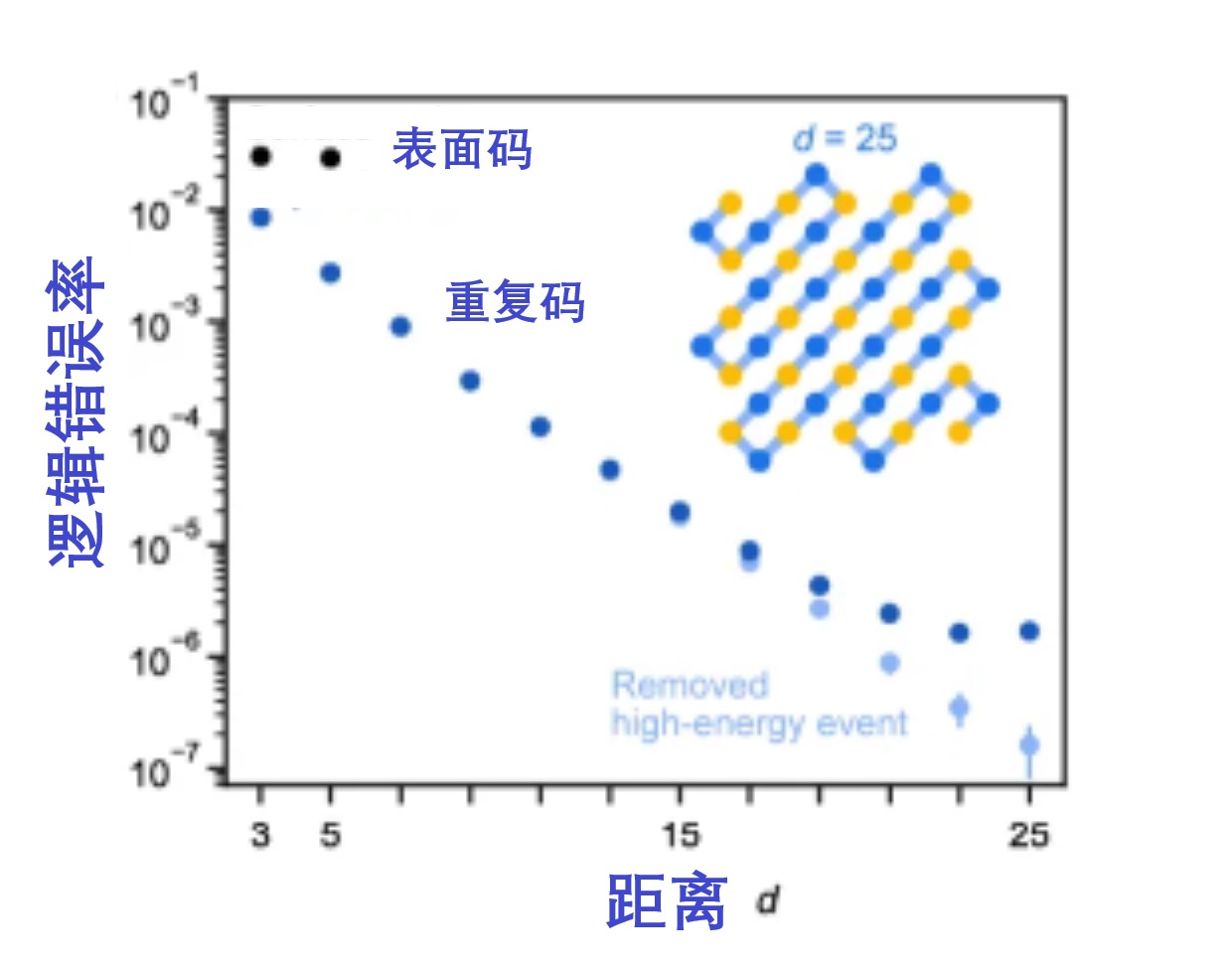
要避免越糾越錯,量子糾錯必須達到一個盈虧平衡點,這個點與糾錯碼的結構有關。糾錯碼的結構中有一個重要的參數d,叫做糾錯碼的距離。距離是在任一維度上跨越代碼的物理量子比特數。距離d越大,需要的冗餘量子比特就越多,糾錯性能便越好。同時,d與另一個參數t有關:2t+1=d,意味着對應距離d的編碼,可以糾正t個比特上的X, Z或者XZ錯誤。例如, 如果一個糾錯碼d=3,得到t=1,意味着可以糾正1個物理量子比特上的錯誤。如果d=5,則t=2,可以糾正2個物理量子比特上的錯誤。一般來說,需要提供的物理量子比特的數目,正比於距離 d的平方,而錯誤率與距離d的關係如圖4所示。
由圖4可見,邏輯量子比特誤差的概率隨着距離d的增加呈指數級下降。但欲使距離增加,又必須增加更多的與d成平方關係的冗餘量子位數目。
圖4:誤碼率vs距離
5.3.4,量子糾錯最新進展
自秀爾之後,為了更有效地利用量子比特,有更多、更高效的糾錯碼被提出和研究,例如圖5所示的Steane碼和表面碼。
通過糾錯,科學家們希望實現的目標是“容錯量子計算”。在這種計算中,建立起足夠的冗餘和適當的編碼,使得即使有幾個量子比特出現錯誤,系統仍能運行並返回準確的答案。量子比特數的擴張,以及量子糾錯技術的重大進展,是實現量子計算的關鍵和挑戰。
所以,量⼦糾錯的思想就是將單個“邏輯”量子比特值在多個物理量子比特之上進行複雜的編碼,合稱為糾錯碼。量⼦糾錯碼有很多種類,各有優缺點。例如上面說的Shor碼,是9個物理量子比特,編碼1個邏輯量子比特。圖5左土的Steane碼,用7個量子比特,編碼一個邏輯量子比特。除此之外,還有表⾯碼、⾊碼、積碼、等。其中的表⾯碼是最常用的一種拓撲碼(圖5右圖)。表面碼由於容錯閾值高、且與二維網格結構完美兼容,近年來被認為是最有潛力和實用價值的量子糾錯碼方案之一。
圖5:量子糾錯的Steane碼和表面碼
從實際操作的角度考慮,俄裔美國物理學家,加州理工學院物理系教授基塔耶夫(Kitaev)提出了量子糾錯表面碼,通過使用二維方格上布局的量子比特來進行編碼和探測,得到良好的糾錯性質。由於超導、離子阱和中性原子等技術,均可實現這種量子比特的布局,表面碼糾錯成為近幾年的研究熱點。除了糾錯碼之外,基塔耶夫對量子計算做出了傑出的貢獻,在朗道理論物理研究所工作時,他引入了量子相位估計算法和拓撲量子計算機,並引入了任意子。他曾獲基礎物理學獎、狄拉克獎等。
表面碼等仍然需要大量的物理量子比特,來編碼一個邏輯量子比特。例如,一個距離為10的表面編碼將需要大約200個物理量子比特來編碼一個邏輯量子比特。2023年之前,表⾯碼需要多達4000個物理量⼦位來構建12個邏輯量⼦位。
所幸的是,2023年底,量子計算技術迎來了幾項重要的突破,包括量子糾錯方面的突破。在2023年12月6日發表於《Nature》的論文中,美國哈佛大學米哈伊爾·盧金(Mikhail Lukin)領導的團隊,採用了一種全新的糾錯方法,將280個物理量子比特轉化為48個邏輯量子比特。這比IBM希望在其下一代芯片中實現的效果要好20倍,比當前技術試圖達到的1,000 比1的比例要高效200倍。哈佛大學的研究人員與MIT等團隊合作,成功在一個具有280個物理量子比特的系統中,製備了1個碼距為7、或者40個碼距為3、或者48個碼距為2的邏輯量子比特,並對上述不同碼距的邏輯量子比特進行了有效的錯誤探測,研究了經過後選擇的邏輯量子比特的性能,為實現更多不受錯誤干擾的邏輯量子比特,提供了重要的技術基礎。
哈佛等團隊的48個邏輯量子比特聽起來似乎還不多,但量子計算機的計算能力是以指數級增長的。總之,2023年量子計算機的一系列研究成果預示出,建造實用量子計算機的競賽正在進入一個新階段。2024年將如何發展,科學家們正拭目以待。 **** 參考文獻 ****
【1】Keynote talk, 1st conference on Physics and Computation, MIT, 1981。(International Journal of Theoretical Physics, 21: 467–488, 1982) 【2】Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein; 殷建平等譯. 第1章 算法在計算機中的作用. 算法導論 原書第3版. 北京: 機械工業出版社. 2013年1月 【3】張天蓉. 世紀幽靈-走近量子糾纏(第二版)[M].合肥:中國科技大學出版社,2020年5月。 【4】Bloch Sphere(wikipedia),https://en.wikipedia.org/wiki/Bloch_sphere 【5】IBM Quantum (2022). estimator primitive (Version x.y.z) [computer software]. https://quantum-computing.ibm.com/ 【6】Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212 【7】無窮的開始: 世界進步的本源,作者:戴維·多伊奇 (David Deutsch), 王艷紅, 張 出版社:人民郵電出版社,出版日期:2014-11-01 【8】真實世界的脈絡,作者: [英] 戴維·多伊奇,出版社: 廣西師範大學出版社,譯者: 梁焰 / 黃雄,出版年: 2002-8 【9】David Deutsch & Richard Jozsa (1992). "Rapid solutions of problems by quantum computation". Proceedings of the Royal Society of London A. 439 (1907): 553–558. 【10】Shor’s algorithm from IBM: https://quantum-computing.ibm.com/composer/docs/iqx/guide/shors-algorithm 【11】Anderson, P. W.; Dayem, A. H. Radio-frequency effects in superconducting thin film bridges. Physical Review Letters. 1964, 13 (6): 195. 【13】Ashkin, A. (1970). "Acceleration and Trapping of Particles by Radiation Pressure". Physical Review Letters. 24 (4): 156–159. 【14】D. Jaksch, et al. (2000). "Fast Quantum Gates for Neutral Atoms". Physical Review Letters. 85 (10): 2208–11. 【15】Ziemer, RodgerE.; Tranter, William H. (17 March 2014). Principles of communication : systems, modulation, and noise (Seventh ed.). Hoboken, New Jersey. 【16】基於超導量子系統的量子糾錯研究進展,Acta Physica Sinica, 71, 240305 (2022) DOI: 10.7498/aps.71.20221824 (全文完) |
|
|
 | |
|
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2023: | 全心之於心腦一體智能化的對調相互作為 | |
| 2023: | 關於現在國際政治發展的邏輯 | |
| 2022: | 豐縣董志民家族的前世今生及其關係網 | |
| 2021: | 我是誰? --十二緣起支簡述 (3) 完 | |
| 2021: | 孤獨中的內在話語 | |
| 2020: | 好文推薦:美國科學家首發布病毒3D圖, | |
| 2019: | “我來晚了,我來晚了” | |
| 2019: | 翟天臨論文曾通過雙盲審 多審查為何失 | |