| 天才科學“玩”家、信息論之父的遊戲人生 |
| 送交者: 天蓉 2024年03月07日12:55:01 於 [教育學術] 發送悄悄話 |
他自稱是一個不關心政治的無神論者,他小時候玩發明,長大後玩數學,老了玩股票,什麼好玩就玩什麼,科學技術領域給玩了個遍。他不在乎這樣東西有沒有實用價值,不管那套理論有無學術意義,不考慮做的事情對公司有無貢獻,不管這個問題是否重要,他只管好玩還是不好玩。他的名字算不上廣為人知,但他被譽為信息論之父。他,就是香農。 愛迪生的小親戚 克勞德·香農 (Claude Shannon,1916年-2001年)出生成長於美國中部密歇根州一個小鎮,有趣的是,香農的父親給兒子取了一個和自己一模一樣的名字[1]。老克勞德·香農是歐洲早期移民的後代,曾自主創業經商並取得成功,還做過當地的遺囑檢驗法官。香農的母親是德裔移民的女兒,當時少見的進過大學的女性,職業是語言學教師,還做過中學校長。香農還有一個姐姐,則得了一個和母親一模一樣的名字。香農一家在小鎮上頗得人心:父母的職業和為人均受人尊敬。比香農大6歲的姐姐是個聽話的孩子,優秀的學生,在學校各門功課成績都很好,是現在被人們稱為“學霸”式的人物。香農呢,他異常瘦弱,身上皮包骨頭、臉龐稜角分明,言語不多,卻又格外聰明,在小城鎮裡,他看起來永遠像是那種剛剛被人欺負毆打過,令人心生同情的年輕小伙。 香農小時候最喜歡玩的是電氣電子機械,他崇拜託馬斯·愛迪生。不過後來他知道了,愛迪生竟然是自己的遠房親戚,便十分引以為傲。 使小香農自豪的,除了大發明家愛迪生之外,還有他的爺爺戴維·香農,爺爺是一位農場主兼發明家,頗具機械方面的才華,他對早期的洗衣機進行了一系列改進,擁有美國第407130號專利。 看來,發明的天賦也是能遺傳的。小玩家香農有着一顆愛發明的心,將撥弄機械當作玩耍,他經常在家裡搗鼓模型飛機、也製作用無線電控制的模型船。除了格外愛玩,他的童年卻也分外孤獨。因為當時他所處的小鎮,人煙稀少,密歇根廣袤的農地中,偶見幾條街道和少許店鋪,最近的朋友,也住在半英里之外。於是,香農發揮他擺弄物件的天賦,自建了一個可以與朋友聯繫的無線電台。香農的經驗不斷積累,高中畢業時,他已經是一名嫻熟的發明家。他的發明包括簡易升降機、後院小推車和通過帶刺鐵絲網傳遞加密消息的電報系統,等等。
圖1:小時候的香農 除了發明小機械外,香農也表現出驚人的數學天賦。據說在8歲的時候,他就能做出他學數學的姐姐的高等數學作業。1934年,香農於17歲的時候,在《美國數學月刊》上發表了他的第一篇學術文章。他解出了一道數學難題,第一次向公眾展示了他的數學才能。既會發明又能數學抽象,這兩點成就了香農,使他造福於人類! “最著名的碩士論文” 1932 年,16歲的香農進入密歇根大學,在他鍾愛又好玩的數學和電子工程兩個專業之間遊蕩,幾年後,20歲的香農獲得了這兩個專業的本科學位。臨近畢業時,公告欄上一則廣告引起了他的興趣。說的是時任麻省理工學院院長萬內瓦爾·布什提供了一個研究生職位,合格者在讀碩士的同時,還需要為布什教授操作管理他的一台微分分析機。據說這是一個重達百噸、由轉動的軸承和齒輪構成的奇怪機器,在新聞中被譽為“機械大腦”或“思考機器” :它能做高等數學,解出人類要花數月才能求解的方程! 那是第一次世界大戰後,世界經濟重心由歐洲轉到美國,貝爾實驗室、通用電氣、麻省理工,成為美國電氣工程應用的三大中心。隨着機械和電氣技術走向成熟,許多領域都對計算有迫切的需求。例如無處不在的微分方程,它們很少能有解析解,枯燥乏味的大量計算令人頭疼。因此,布什教授設計了“微分分析機”來解決此類難題。用如今的術語來說,這部機器是模擬的而非數字的,其輪盤式積分器便是微分方程的物理模擬。無論如何,機器在當年還是很有用處,師生們蜂擁而來,排長隊求用它以解決工程中的難題。布什已經難以應付,所以急需一名助手來操作、研究、和改進這個機器。 這個消息對臨近畢業的香農來說,當然是天上掉餡餅,一個求之不得的好機會。而布什得到香農這樣的機械電氣都懂的全才也是正中下懷。於是,香農順利進入麻省理工學院深造,那年頭,MIT的校園裡,便多了一道風景!香農“玩”名遠播,有人說:這個校園裡,如果你看見一個年輕人,目光深邃面龐瘦削,騎着一架怪異的獨輪車,從你身旁飛駛而過,那多半是香農!
圖2:香農和MIT的微分分析機(MIT Museum) 香農很快就深深地迷上了這架大玩具。那些旋轉不止的模擬部件,分布在一個大大的平台式機器上,電源插上機器啟動,整個房間喳喳作響。這種人們不喜歡的噪聲,卻令發明家欣喜無比。 微分分析儀是由布什和哈森於 1928 年到 1931 年建造的。兩位工程師製造它是為了解決應用數學和物理領域中的實際問題,即求解微分方程。這實際上是一台由傳動軸、齒輪和轉盤組成的複雜的模擬計算機。在工程和物理學的動態系統中,如果兩個物理量之間有某種數學關係,例如微分或積分的關係,便可以從這個動態系統的實際運作來完成該種數學計算,稱之為模擬計算,該系統便是一台模擬計算機。
圖3:模擬積分器 (https://sinclairtarget.com/differential-analyzer/) 布什的MIT微分分析儀最重要的構件是六個積分器,機械積分器的歷史可以追溯到 19 世紀,它能夠用動態系統中具積分函數關係的兩個物理量,來模擬積分運算。機械積分器基本上是一個特別的求和機器,見圖3。每一個積分器對應一個一階微分方程。布什發現了一種將積分器串聯起來解決高階微分方程的方法。因此,他的包括六個積分器的微分分析儀,能夠求解高達六階的微分方程。 香農喜歡機械,當然對微分分析儀感興趣,布什供給了許多元器件,希望香農能將機器朝更通用更自動化的方向改進,香農打算用上百個繼電器來達到目的。他看着那些似乎不作聲又偶爾咔嚓一下的繼電器,覺得十分有趣。香農腦海中浮現出傳遞信息的摩爾斯碼,繼電器很像發送摩爾斯碼使用的開關,香農又回憶起不久前上過的一門符號邏輯課程,其中有布爾代數。 布爾代數得名於自學成材的英國數學家布爾,他在1847年出版的一個小冊子中介紹了這種代數邏輯系統,人們覺得這很有趣,但似乎沒有什麼實際用處。美國邏輯學家皮爾士曾經提出可以通過電氣開關進行布爾計算,也沒得到廣泛的響應。 開關是電路器件,布爾邏輯是數學運算,兩者看上去似乎風馬牛不相及,但香農卻感覺似曾相識,覺得這兩者有相通之處,他想,這其中也許有文章可做! 接着,香農在1937年夏,到紐約的貝爾實驗室實習了一個暑假,有關開關和布爾邏輯,這些令人困擾的想法,在他腦海里一直揮之不去。 香農進一步思考後發現,繼電器“開、關”,或“是、否”,其實並不重要,關鍵的是這兩種類型連在一起時,可以被邏輯中的“和”、 “或”、 “非”等等表述出來。例如,兩開關串聯即是“和”,並聯則是“或”。其實,這就是在做計算。也就是說,電路可以進行邏輯運算! 布爾代數中的每個概念在電路中都有相對應的物理表示。操作電路繼電器的人在實際上知道這些電路原則,但他們沒有把他們所做的事情抽象成布爾代數的數學模型。因此,布爾邏輯可以實現到符號再到電路的飛躍。只要定義好了邏輯符號,由繼電器組成的複雜電路的效應,便可以表示成多個變量二進制的代數方程式。比如,以下方程式: x'y'z + x'yz + xy'z + xyz' + xyz 可以表示一個3個繼電器構成的電路。 這個21歲的青年,覺得這個想法非常有趣,他興奮激動於自己從開關盒子和繼電器中看到了別人沒有看到的東西。1937年秋,香農在美國華盛頓哥倫比亞特區向評委會演示了自己的碩士論文《繼電器和開關電路的符號分析》,並在第二年發表在期刊上。 香農在論文中,分析了電話交換電路和布爾代數之間的類似性,用布爾代數分析並優化了開關電路。香農的這篇碩士論文,具有劃時代的意義。它奠定了數字電路的理論基礎。因此,有科學家評價這篇論文是“有史以來最重要的一篇碩士論文”,“從藝術到科學上改變了電路的設計” 。香農將電路設計的技術變成了一門科學! 因為這篇論文,香農獲得了電子工程界的大獎——美國Alfred Noble協會的美國工程師獎。這給香農帶來了在電子工業界大展拳腳的好機會,然而,他卻似乎從這個領域消失了。 香農於1939年夏天,來到了冷泉港,抵達了美國最頂尖的基因實驗室。原來他改弦更張,從電子工程跨界到了生物,試圖將他的“代數”理論應用於新興的遺傳學,他玩起基因來了!兩年後,他完成了博士論文——《理論遺傳學的代數》,用線性代數描述不同遺傳性狀在遺傳中的可能性,用一種奇怪的符號代數,來預測性狀是如何代代相傳的。
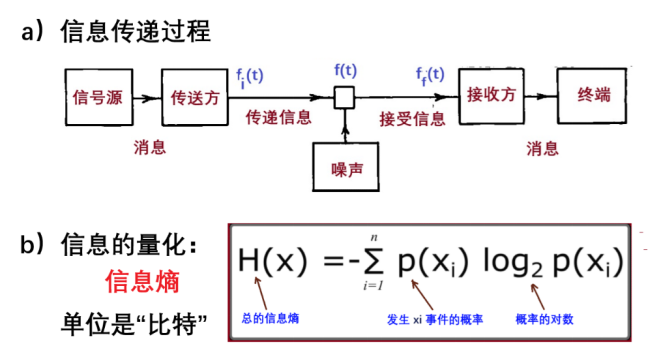
圖4:香農的博士論文丨圖源:dspace.mit.edu 那時候,尚未發現DNA螺旋結構,也不知道遺傳密碼等等,香農是完全在自己頭腦中構想遺傳機制的,並企圖用代數理論模型去描述遺傳現象。 1940年香農以此論文,獲得了麻省理工的數學博士學位,並且得到了普林斯頓高等研究院的博士後機會。在那兒,香農能自由地跨學科工作,他有機會與外爾和馮·諾依曼等數學家討論他的想法,還偶爾遇到愛因斯坦和哥德爾[2]。 計算、密碼、信息 被譽為計算機之父,比香農大4歲的圖靈,比香農更為公眾所知。但實際上,他們兩人的思想和經歷有很多相似之處:都對機器計算感興趣,都研究過密碼,都曾經將數學應用於生物學,都喜歡思考人工智能的問題,等等。遺憾的是,他們一個在英國一個在美國,生前很少見面。感慨的是他們後來的境遇:圖靈因性取向受迫害早逝,香農“玩”到八十多歲高齡,老年痴呆去世。 二戰期間的1943年初,在美國貝爾實驗室的餐廳里,兩位天才少年一見如故。圖靈那年被派往美國,來到新澤西,目的是為了給大西洋兩岸傳輸的通話內容加密,使敵人無法監聽盟軍情報。香農戰時從普林斯頓高等研究院,轉到了貝爾實驗室,研究如何對華盛頓到倫敦的通信線路進行加密的課題。儘管我們現在知道他們那時都在研究密碼,但各自的專題項目,分別是兩個國家的絕對機密,所以兩人都不知道對方在搞啥?飯堂里的閒聊也不涉及解密技術。不過,他們有太多的共同話題和想法,那些日子他們閒聊的是“會思考的機器”,也就是理想的計算機的極限是什麼的問題。那年代還沒有人知道計算機到底將是什麼模樣!所以他們的探討大多基於數學和邏輯,兩人想都沒想過,他們將在科學史上各自開闢一個獨立的領域。 圖靈從更為數學的視角出發,認為理想的計算機應該是純粹邏輯演繹的設備,而熱衷於發明的香農則考慮得更廣泛,他認為計算機將是一種社會性的工具,甚至能處理音樂等非邏輯性的東西。 於是,圖靈向香農展示了他 1936 年的論文,就是定義了現在所謂的“通用圖靈機”的那篇文章。這給香農留下了深刻的印象,因為其中的許多想法與他自己的想法不謀而合相輔相成。圖靈的工作使香農靈感忽現,他發現,有些看似截然不同的事物其實具有共同的本質。 圖靈在與香農交流“通用圖靈機”的過程中也大為振奮,兩人討論時說話的聲音不由自主地越來越大,甚至引起周圍用餐人紛紛注目。香農從電子工程師的視角,看到了圖靈機的實用價值,這點使圖靈激動不已,也讓圖靈站到數學之外,對圖靈機的意義重新思考。會思考的機器,或許真的可以用電路而變成現實嗎?圖靈覺得這太有趣了!因此,他在離開美國之前,買了一本電路入門書,把它帶到回英國的船上,如饑似渴地閱讀起來。 圖靈在密碼方面的工作主要是破解了德國人發明的ENIGMA密碼,這種密碼被德軍廣泛使用,包括定位出沒於大西洋運輸線上的潛艇。當年的英國人和法國人都認為ENIGMA是不可破譯的,圖靈率領着大約200多名精幹人員進行密碼分析,他們掌握了破譯該密碼的一整套方法,從而了解了德軍的動向,掌握了戰爭的主動權,為英美聯軍擊敗德國做出了突出貢獻。 香農在密碼學方面的工作,則與其後來關於通信理論的關係密切。香農自己說,他對通信理論和密碼學的戰時見解是同時發展的,“它們是如此緊密地結合在一起,你無法將它們分開”。 實際上,香農更早就有了模糊的想法。在1939年初,他在寫給布什的信中說到,除了微分分析機外,他還在考慮一個自認為更重要的問題:“我一直在研究傳遞信息的一般系統的某些基本屬性,它們包括電話、廣播、電視和電報等。幾乎所有的通信系統都可以歸結為如下的一般形式:信息從發送方到接收方,其中涉及三個“時間函數”,待傳輸的初始信息fi(t),中間信號f(t),以及最終輸出ff(t)。”,這就是香農設想的通訊過程,見圖5a。
圖5:信息論 香農認識到,真實的系統中還存在噪聲,並且他試圖證明一些定理,來數學地描述通信系統。在貝爾實驗室,研究數字通信中的信息保密和隱藏技術的一系列工作,成就香農建立了現代信息論。1948年,作為此項工作的總結報告,香農發表了論文“通信的數學原理”[3],1949年,他又發表了“噪聲下的通信”一文。幾篇文章闡述了信息論的基本內容。 我認為信息論是科學中最美的理論之一,它美在哪裡呢?美在其通用性,美在它的簡潔,並且,尤為可貴的是:它美在簡潔與深奧並存[4]。 圖5中簡單的兩個圖,就幾乎概括了信息論的全部內容。其中的圖a描述了信息的傳輸過程,這不僅適宜於通訊,還有計算機、遺傳學、生物學、物理及化學過程等。事實上,信息及其傳輸過程無處不在,因此,信息論幾乎可以推廣應用到所有領域。 如何用數學語言描述信息傳輸過程?為此香農定義了信息的基本概念,見圖5b。 什麼是信息?信息的概念既抽象又多變,信息既不是物質,也不是能量,要給信息這個人人明白又抓不住摸不着的東西,下確切定義是不容易的。可以毫不誇張地說:幸虧有了香農!作為玩遍種種技術的工程師,香農深刻理解“信息”之本質;作為善於抽象的數學家,香農明白必須首先給信息一個定量描述,量化後才有理論!物質和能量都是可度量的,如何度量信息呢? 香農借用了熱力學中的一個詞:熵。或許在學術界關於信息理論的辯論中,馮·諾爾曼和維納( Wiener)對香農都有所啟發,但無論如何,是香農最終提出了“信息熵”的概念和表達式(圖5b)。信息熵公式中,香農天才而巧妙地將信息與概率聯繫起來,揭示了信息是“不確定性的度量”這個微觀本質。 用過計算機的人對“比特”這個詞不會陌生,但你可能不知道,比特是香農定義的信息的單位,計算過程就是傳遞信息,所以自然而然地,比特也成為了衡量計算機運算及儲存能力的重要指標。 這兒舉“語言信息”為例,簡單理解一下圖5b的公式。例如,人們說一句話,其中的信息是一個“字符串”,例如“我是馬斯克”,這是5個漢字符號組成的字符串。信息熵H是由字符串中所有符號xi的概率p(xi)乘以概率的對數再求和所確定的,每個符號xi的信息量,與符號通常出現的概率(不確定性)有關。因此,香農的信息論公式,在信息與不確定性和混亂程度之間架起了橋梁,這是信息與自然界的深層聯繫。 傳奇人物銷聲斂跡 這兩年最火的科學新聞首推“AI”,即人工智能,殊不知香農也是AI先驅之一。 香農在 1950 年左右發表的一篇論文《計算機下棋程序》裡描述了如何讓計算機下國際象棋。此文被認為是最早發表的關於計算機下棋和使用計算機解決遊戲主題的文章之一,其中他提出了限制國際象棋遊戲中要考慮的可能性數量的基本策略。香農給出了國際象棋的複雜度,大約是 10¹²⁰ 量級(被稱為“香農數”),不過他在論文中給出了一個更為明智的算法,可以大幅度地簡化計算。1997 年,由這篇論文演化出來的算法,在“深藍”中運行,成功擊敗了卡斯帕羅夫。 香農大多數學術成果都是上世紀60年代之前完成的,然後,他就不“玩”學術而玩別的去了。
圖6:愛“玩”的香農(圖片來自網絡) “你無憂無慮的秘訣是什麼?”一位採訪者在香農臨終前詢問他,香農回答說:“我一生順其自然,實用性不是我的主要目標……”。總結香農能無憂無慮地“玩”,首先肯定是拋棄了世俗名利的紛擾,好奇心驅動他對大自然的探索。終其一生,香農都在玩遊戲、發明遊戲、擺弄小機械和小裝置,即便成年之後也保持着那份童真之心。 1951年,香農發表論文“介紹一個走迷宮的機器”,寫的是他製造的名為“忒修斯”(Theseus)的機器老鼠,迷宮配置靈活,可重新布置任意修改。機械鼠在 25 個方格迷宮中移動,通過反覆試探後自己找到迷宮的出路。老鼠第一次穿過迷宮後,如果將它放置在之前去過的地方,它可以根據之前的經驗,直接就到達目標。如果被放置在不熟悉的區域的話,便會被編程為“搜索”,然後逐步搜索直到成功。成功後,它會將新知識添加到其記憶中並學習新的行為,你看看,這像不像如今的AI學習機器? 香農是一個狂熱的獨輪車愛好者,他喜歡設計和製造各種稀奇古怪的獨輪車。他發明了名為 THROBAC 的羅馬數字計算機和雜耍機;他建造了一個可以解決魔方難題的設備;他還與索普共同發明了第一台可穿戴計算機,用於提高玩輪盤賭時的賠率。他設計了一個“心靈閱讀”機器,通過觀察和分析弈棋對手過去所做各種選擇的樣本,能夠相當準確地猜測到對手下一步棋的走法。 雖然香農一直是MIT教授,但因為痴迷玩發明創造,後來他不發論文也不出席專業會議,便逐漸淡出了公眾的視線。非常戲劇性的一刻發生在1985年的英國國際信息理論研討會上:香農出人意料地現身會場,很多與會者甚至不知道他仍然在世。這位謙虛羞澀的名人被人認出來後,被粉絲們團團圍住。最後,還只好不情願地在晚宴上登台,被主持人隆重地介紹為“我們這個時代最偉大的科學巨匠之一”。掌聲平息後,香農冒出一句:“這真是太可笑了!”然後,他把手伸到衣服口袋裡,變戲法一樣掏出了3個球,竟然當場玩起了雜耍。 會玩雜耍的人千千萬,世界上的發明家也不計其數。然而,會玩又能從中悟出大自然奧妙的人,唯香農也。誰能玩密碼聯想到信息論?又有誰玩象棋時思考AI?誰能玩了拋球雜技便提出一個“拋球定理”?哪一個獨輪車騎手,非要將獨輪車的運動轉化為方程式呢?別無他人,唯香農也。 到了1980年代,香農的記憶力開始嚴重衰退,後來患上了老年痴呆症。這位獨特而有趣的天才,在與疾病抗爭了很長一段時間後,於2001年2月24日辭世,享年84歲。 參考文獻: [1]香農傳,作者:[美]吉米·索尼,[美]羅伯·古德曼譯者:楊曄出版社:中信出版集團出版時間:2019-02 [2]信息簡史,作者:[美]詹姆斯·格雷克譯者:高博出版社:人民郵電出版社出版時間:2013-12 [3]Shannon C E. A mathematical theory of communication[J]. ACM SIGMOBILE Mobile Computing and Communications Review, 2001, 5(1): 3-55. [4]科學網—“熵”- 信息世界也逞強- 張天蓉的博文: https://blog.sciencenet.cn/home.php?mod=space&uid=677221&do=blog&quickforward=1&id=987651 (本文於2/3/2024首次發布於微信公眾號“知識分子”) |
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2023: | 用意識形態武裝起來的盜賊---東海客廳 | |
| 2023: | Nanjing 2023 Tour,好看 | |
| 2022: | 戰略分析(8):普京的出現是北約難得 | |
| 2022: | 分享21種俄語詞典(Txt格式) | |
| 2021: | 萬景路:民國時期旅日文化人眼中的日本 | |
| 2021: | 藝術座談 (2) - 藝術的兩重性 | |
| 2020: | Instancology English 範例口語 | |
| 2020: | 879北宋宰相韓琦的29代孫、宋美齡之父- | |
| 2019: | 中國走向文明、走向世界的兩大阻力 | |
| 2019: | 619、質速公式;百花公主;舊歡如夢 | |