从此便有了可逆计算的概念。什么是可逆计算?经典计算由电子电路实现,那么,什么样的电路是可逆电路呢?通俗地说,一个电路是可逆的,就是说如果将输入与输出交换一下,从输出的值可以得到输入的值。举个最简单的例子,图2的左上图·,是一个不包括进位的十进制加法器S=A+B,如果将输入输出交换一下,成了右上图。然而,看看图2的右上图就发现,从输出不能唯一地还原输入。例如你用S=7+3得到10,但用10作为输入,你不能唯一地得到7和3!因此,我们就说图2左上图的电路是不可逆的。不过,使用一个额外的输出端P=A,就将图2的左上图变成了两个输入两个输出的左下图。虽然增加的这个输出端没有作任何运算,只是直接输出A而已,但却把原来的不可逆电路变成了可逆电路。因为当我们将输入输出交换一下,成为右下图时,可以还原原来的输入值7和3。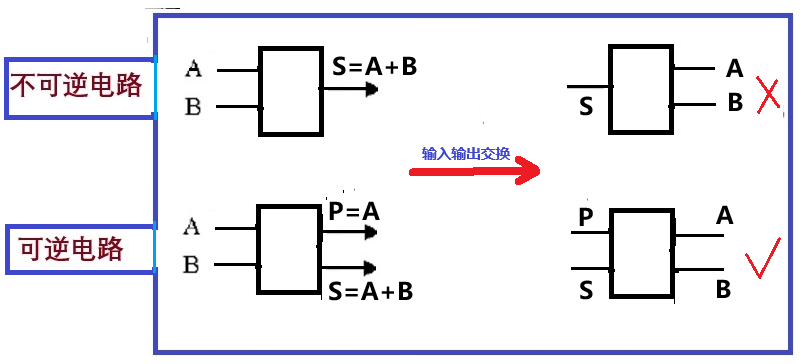
▲ 图2 不可逆与可逆计算的简单例子
图2例子的重点在于,输入端和输出端数目不相等的电路,一定是不可逆的电路。但可以增加额外的端口,将不可逆线路变成可逆的。要增加几个端口,得看具体情况而定。图2例子用的是10进制,对2进制逻辑,原则上是一样的。例如图1最下面的图中,左边的异或门是2比特输入,1比特输出的经典门,输入输出端数目不相等,当然不能交换,所以不可逆。但这个经典的不可逆异或门电路,可以用增加一个输出端P的办法,改造成可逆异或门,如图1下图中右边的电路(两个输入端,两个输出端)所示。现代计算机是许多“bit”构成的十分复杂的布尔逻辑电路,一般都不可逆,所以要耗散很多能量。但是,如果将电路加上许多额外的“比特位”,就可以将经典计算机重新设计成可逆的经典计算机,让能量耗散达到最小。微观来说,可逆的意思就是要“初态”与“末态”一一对应,才能保证在计算过程中不引入任何新的不确定性,可以让系统“原路返回”。这要求执行计算的物理系统满足时间反演对称性,还要求系统与环境完全隔绝。但是在实际计算中,不存在这样的物理系统,因而便有了“计算导致熵增加”的兰道尔原理。用一个比喻来说,可逆计算就如同可逆的卡诺热机一样只有理论上的意义。在实际中很难实现这样理想化的模型。因此,兰道尔原理的直接后果是导致所谓摩尔定律的终结。因为现有的不可逆计算机物理上必须消耗能量,并以热量的形式散发。当计算的速度越快或集成元件数目越多,产生的热量就越多。兰道尔等提出的可逆计算概念突破了这种极限。1973年,贝奈特证明了那种不要擦除信息的逻辑上可逆的计算原则上是可行的,经典计算可以靠改进电路来实现可逆,就如上面两个例子中的电路那样,而以下我们会提到:量子计算本质上就是可逆的。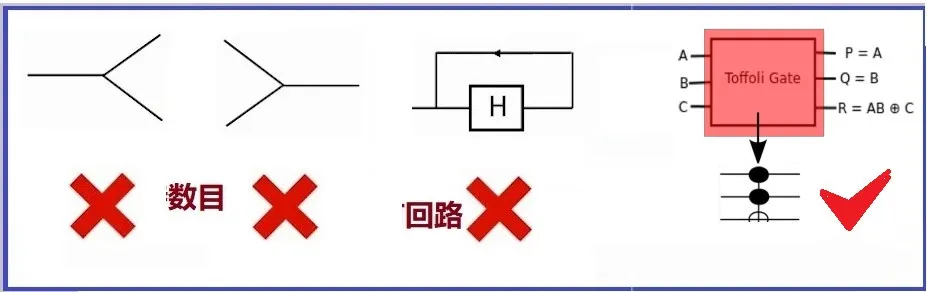
▲ 图3 不可逆逻辑门和可逆逻辑门
因此,人们从两个不同的侧重点提出了量子计算的想法:费曼从模拟的角度,而兰道尔等从计算的可逆性(图3),即受热力学限制的物理极限之考量。
研究量子信息和量子计算,还有第三个目的,不仅仅出于实用的需要,也涉及到从物理理论的层面上深入理解信息、物质、能量的关系等基础问题,并有助于更好地诠释量子理论。
对早期的科学家来说,信息的概念十分缥缈抽象而空灵,直到香农的信息论问世,才将“信息“解释为不确定性的度量。兰道尔原理更为真实地将信息与物质及能量的概念联系起来,正如兰道尔经常告诫他的IBM同事:”信息不可避免地是物理的,信息植根于现实世界,必须通过应用严肃的物理定律来理解。”
“兰道尔是一位老IBM类型,做事正直、狭窄,对那些足以成为时尚但过于宏大和简单无用的想法有着敏锐的洞察力。”贝内特博士如此回忆他的朋友和同事。
兰道尔1961年发现兰道尔原理后,有几位物理学家研究过可逆计算。例如,在德国计算机专家楚泽(Konrad Zuse)的书《计算空间》(1969年)中,提到了可逆计算的重要性。认为在这种可逆计算模型中,使用的能量很低,熵的增加会最小化。
1972年,兰道尔和贝内特,从理论上证明了计算机以可逆方式执行计算可以避免熵的增加。后来发现,另一位MIT的教授埃德·弗雷德金(Ed Fredkin,1934-2023)独立地得出了同样的结论。弗雷德金更进一步,他发明了一个Fredkin门,后来托弗利又发明了Toffoli门,这两种门代表了可逆电路研究中根本性的突破,有了它们,才使得可逆的经典计算机得以具体实现。这两种门是通用的,使用它们可以实现所有的可逆布尔函数[3]。Fredkin门是⼀个3×3可逆门,输出为P=A、Q=AB+AC和R=AB+AC,保留了一个输入端(P=A);Toffoli门是具有三个输入端的可控非门,保留了两个输入端,见图4。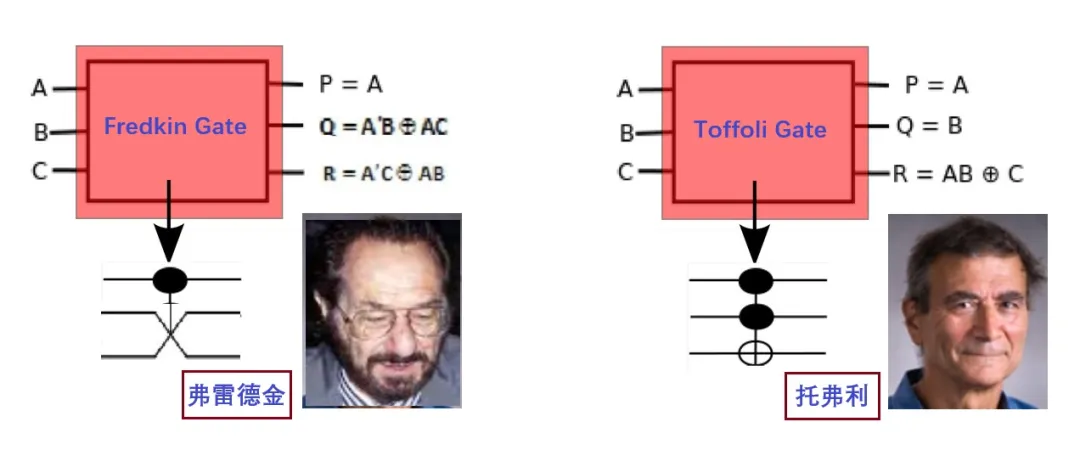
▲ 图4 弗雷德金门和托弗利门
我们之前介绍过的弗雷德金,是美国计算机科学家和商人,是数字物理学的早期先驱。托弗利(Toffoli,1943-)是一位意大利人,1969年移居美国,之后成为了美国计算机工程教授。托弗利1976年在意大利获得了第一个博士学位,研究领域是宇宙射线探测器的电子器件。他在美国的密西根大学与Art Burks(图5右)一起研究二维元胞自动机,数学家阿特·伯克斯Art Burks是“元胞自动机”这个名字的创造者。此外,托弗利对可逆计算感兴趣,写了一篇论文,展示了如何通过存储普通计算机必须忘记的所有内容来构建可逆计算机。正当他1978年刚刚完成他的第二个博士学位之时,他的可逆计算文章被MIT的弗雷德金教授发现了。该论文令弗雷德金对托弗利注目,因为当年作可逆计算及元胞自动机的人不算多,真正设想具体实现的人更是寥寥无几,托弗利是其中之一。于是,弗雷德金决定雇用托弗利来帮助自己研究可逆计算。后来,弗雷德金用他获得的DARPA的一笔资助,支持Toffoli和弗雷德金在MIT的一位唯一的“物理学博士生”,Norm Margolus,建造了一个越来越大的“细胞自动机”。因此,弗雷德金将Toffoli带到了麻省理工学院,1981年,他们两人都出现在MIT的著名会议上(图5)。他们在MIT建造了一台元胞自动机,还合作写了一篇关于保守逻辑的论文,最终于1982年发表,其中包含弗雷德金门和托弗利门。托弗利门可以算是弗莱德金门的一个特例,两种门可以加上其它基本逻辑门而互相转换。Toffoli的⼯作挑战了可逆计算中不允许反馈的观念,并为可逆逻辑电路设计的研究开辟了新途径。他的结果表明,通过仔细设计电路的组合部分,可以引⼊反馈并仍然保持可逆性。这导致了更先进的可逆逻辑电路的发展,这些电路能够实现复杂的操作,同时仍然保持较低的量⼦成本。
▲ 图5 MIT会上与可逆计算有关的几位科学家
在MIT,托弗利作为一名研究科学家,从1978年开始,工作了近二十年。其间托弗利不仅研究可逆计算机,也将可逆的概念首次引用到元胞自动机中,提出了可逆元胞自动机的概念。但是,可逆计算机或细胞自动机,都不是当年麻省理工学院计算机研究的主要课题。最后,这个项目被关闭了,托弗利1995年转到波士顿大学成为教授。近年来,经典计算系统的可逆逻辑重新受到关注,因为其降低功耗的能力,在低功耗CMOS设计、光学信息处理、DNA计算、量子计算和纳米技术等方面有着广泛的应用。特别是在新型的纳米技术中,可逆逻辑可以显着减少的能量耗散,确保计算过程中不会丢失任何信息,从而避免因散热而浪费能量,这不仅提高计算的效率,也有利于环保。例如在可穿戴和便携式设备中,应用可逆计算的思想,可以将能量耗散降低到最小。
本文到此为止,说的都是经典的可逆计算。那么,量子电路中可逆性的概念又是什么?为什么它在量子计算中很重要?量子现象与经典现象完全不同,因而描述它们的数学理论也不一样[4]。两种理论的一个重要区别就是物理量的算符化。在经典物理中也使用算符,比如平移算符、旋转算符等,但是算符对经典物理而言,是为了方便,对量子力学而言却是不可或缺的。因为在经典物理学中,诸如粒子的坐标、动量、能量、角动量等力学量,理论上有明确的定义,实验测量有确定的数值。而在量子力学中,即使研究的对象只有1个粒子,它的运动也需要用弥漫整个时空的波函数来描述。因此,物理量的经典概念必须加以改造方能使用,算符化便是一种改造方式。也就是说,量子理论中的物理量被作用在波函数上的算符所替代,这样更容易描述量子规律。在量子理论的统计诠释下,每次实验测到的物理量数值不是确定的,而只是以一定几率出现的算符的本征值中的1个。在量子物理中,物理量的状态(量子态)用算符来表示,状态与状态之间的转换(计算门)也是用算符来表示,它们是两类不同的算符。量子力学中的可观测量都是由厄米算符来表示,表示量子态之间的转换的,叫做幺正算符,或酉算符。用通俗点的实数矩阵表示来说,就分别对应于自共轭矩阵和正交矩阵。计算的过程就是物理状态变换的过程,这种变换用各种“量子门电路”来实现。因此,量子门便对应于酉变换。厄密算符的本征值为实数,因而才能在量子力学中描述与经典物理量相对应的可观测量。物理量间的变换为酉变换,它的幺正性(Unitarity)指的是于时刻t在全空间找到某个粒子的总概率等于1,即归一化条件。因此,酉变换描述的是微观过程的物质不灭原理。酉变换是可逆的,这个特性确保了量子态的演化始终是可逆的,所以说,量子计算天生可逆。而对经典可逆计算机的研究成果(逻辑构造)可以方便地用到量子计算中,只需要认真考虑量子信息相对于经典信息的不同之处即可,尤其是“量子比特”相对于“比特”之不同,这是我们下一篇文章的内容。






