| 費馬大定理證明了全世界數學家都是白痴 |
| 送交者: 沒有用的 2025月06月20日18:04:14 於 [教育學術] 發送悄悄話 |
| 回 答: 費馬大定理-鋪平道路 由 天蓉 於 2024-12-03 16:28:12 |
|
https://blog.creaders.net/u/15205/201811/335501.html 摘要:費馬大定理是一個主項為集合概念的命題,只能是對不同 的變量n去一個個地解決,因為世界上所有的數學定理的主項都是普遍 概念或者單獨概念。世界上沒有任何一個數學定理的主項是集合概念。 國際數學界對費馬大定理的證明錯誤百出,一無是處!它不僅僅違反了 三段論公理,還錯誤地使用反證法,反推時沒有逆行傳遞性,表明整個 國際數學界缺乏正確的邏輯思維。費馬大定理與黎曼猜想的主項都是 集合概念,一個是水中月,一個是鏡中花,都是無法一次性證明的命 題(為什麼要強調“概念”?高斯說“在數學中最重要的不是符號, 而是概念”)。
關鍵詞:費馬大定理,集合概念,三段論公理 一,預備知識:數學命題的主項必須是普遍概念或者 單獨概念 全世界的數學定理的主項都是普遍概念或者單獨概念,世界上 沒有任何一個數學定理的主項是集合概念。 1, 概念的種類 (1),單獨概念和普遍概念 a,單獨概念,反映獨一無二的概念,單獨概念的外延只有 一個。例如,上海,孫中山,,,。它們反映的概念都是獨一無二的。 數學中的單獨概念有“e”“Π”。“e是超越數”就是一個單獨概念的 命題。 b,普遍概念,普遍概念反映的是一個對象以上的概念,反映 的是一個“類”,這個詞項的內涵由為了包含在詞項外延所必須具有的 事物的性質組成。就是說,普遍概念的每一個個體必然具有這個概念的 基本屬性。例如:工人,無論“石油工人”,“鋼鐵工人”,還是“中 國工人”,“德國工人”,它們必然地具有“工人”的基本屬性。數學 中的普遍概念有例如“素數”,“合數”,等。“素數無窮多”就是一 個普遍概念的命題。數學證明對象全部都是普遍概念或者單獨概念。 (2),集合概念和非集合概念。 a,集合概念反映的是集合體,這個詞項的外延由詞項所應用的事物集 合組成,例如“中國工人階級”,集合體的每一個個體不是必然具備集 合體的基本屬性,例如某一個“中國工人”,不是必然具有“中國工人 階級”的基本屬性。集合概念的命題是不需要證明的,也是無法證明的 ,只能是歸納總結。 b,非集合概念(省略)。 2,為什麼數學證明的對象只能是普遍概念或者單獨概念 這是因為數學家的武器級別都是一個“類”,即:定理,公理都是普遍 概念,只能攻擊同樣級別的命題主項。而“集合概念”是一群類,是一 群普遍概念。就好比一個人無法戰勝一群敵人,而這個一群有可能是無 窮多個類。 這個問題也影響了希爾伯特第十問題:不定方程有無整數解的判定是否 可行。增加了一個結論:主項是集合概念的命題不能證明是可以判定的。
二,費馬大定理的主項是什麼概念的命題 1,費馬大定理是一個集合概念的命題 對於>2的自然數,費馬說沒有 整數解,由於n=3, 4, 5, ...以致無 窮,當然屬於集合概念,應該從=3,4, 5,....逐一證明。那麼,安德 魯懷爾斯和其他數學家共同完成的證明是否成立? 2,轉換命題 請注意他的證明方法,他證明的是:假如存在一個反例 ,注意,反例只要一個就夠了,
格哈德.弗賴將方程(1)轉換成 為一個普遍概念的橢圓曲線方程:如果費馬大定理是錯誤的,那麼,至 少有一個解,
經過一系列演算程式,使得這個假設 解(反例)的費馬方程變成:
他指出這裡實際上是一個橢圓方程:
注意,(3)式是一個普遍概念。所有的橢圓方程都具有這個性質。 橢圓曲線是域上虧格為1的光滑射影曲線,它的(仿射)方程,通常稱為 維爾斯特拉斯方程,可以寫成(3)式。 三,錯誤的邏輯 看看那些所謂的數學家們是怎樣推導的(費馬大定理—一個 困惑了世間智者358年的謎): 費馬大定理有反例則弗賴橢圓曲線方程成立。 弗賴橢圓方程不能模形式化(肯.黎貝1985年證明了弗賴橢圓方程不能 模形式化)。 谷山志村猜想斷言每一個橢圓方程都可以模形式化。
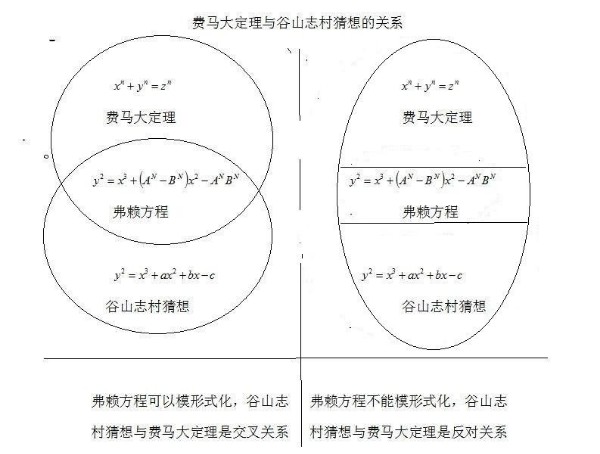
因此得出結論:弗賴方程不能成立(即原先假設的反例不能成立),所 以費馬大定理成立。 上面的推理錯誤百出,因為: 三段論: 大前提:(谷山——志村斷言)每一個橢圓方程必然可以模形式化 (全稱肯定判斷A)。 小前提:弗賴橢圓方程不能模形式化。(肯.黎貝證明了這個 問題) 結論:(只能得出) 1,所以弗賴方程不是橢圓方程(特稱否定判斷O)。 2,谷山志村猜想不能成立。 就是說,肯黎貝定理與谷山志村猜想只能有一個正確,一個錯誤,不會 兩個都是正確的。 並且,國際數學界的推理還違反了演繹推理三段論的規則: 大前提:存在否定費馬大定理的反例-弗賴橢圓曲線方程。【特稱判斷】。 小前提:弗賴橢圓方程不能模形式化(即弗賴方程不能成立)【否定判斷】。 結論:費馬大定理成立【全稱肯定判斷】。 根據邏輯規則:1,如果大前提是特稱判斷,小前提是否定判斷,不能 得出結論。2,在兩個否定的前提中不能得出結論。3,(一共有8條)。所以費馬大定 理成立的結論是荒唐的。 四,費馬大定理與谷山志村猜想的關係 弗賴方程只有被模形式化,谷山—志村猜想才與費馬大定理 是交叉關係,費馬大定理才可能有反例,並不是必然有反例。 如果弗賴方程不能模形式化,費馬大定理與谷山志村猜想是反 對關係。 肯.黎貝定理(弗賴橢圓方程不能模形式化)與谷山志村猜想(每一個 橢圓方程都可以模形式化)只能有一個是正確的,一個是錯誤的。
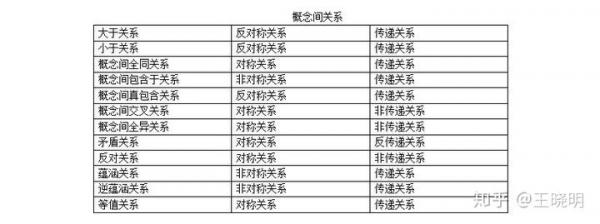
就是說,弗賴方程無論是否可以模形式化,都推不出費馬 大定理是成立或者不成立。為什麼?因為: 概念間交叉關係,是一種對稱關係,是一種非傳遞關係,谷山志 村猜想對與錯都不能傳遞到費馬大定理的對與錯; 概念間的反對關係是一種對稱關係,是一種非傳遞關係,谷山志村 猜想對與錯都不能傳遞到費馬大定理的對與錯。 (概念之間的關係是中國政府公務員歷年考試題目,有1000萬中國青年 學 習過這個內容,絕大多數考試的中國青年不會搞錯,下面是概念之間邏 輯關係)
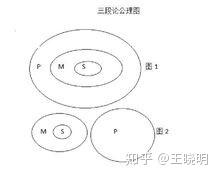
五,違反了三段論公理 國際數學界的推理違反了三段論公理。 根據,三段論公理: 凡是對一類事物性質有所肯定,則對該類事物中的每一個分子的性質也 應該有所肯定; 凡是對一類事物性質有所否定,則對該類事物中的每一個分子的性質也 應該有所否定。 從概念的外延方面看,
圖1表示:s類包含於m類,m類包含於p類,所以,s類包含於p類; 圖2表示:s類包含於m類,m類與p類全異,所以,s類與p類全異。 三段論公理的客觀基礎就是類與類的包含關係和全異關係,是人類 億萬次重複實踐中總結出來的不證自明的性質。 我們設圖中的: M = S = 如果M具有性質P(模形式化),S卻不具有性質P,得出了違反公理的結 論。也說明了谷山志村猜想證明有錯誤。 好比說浙江省屬於中國,杭州市屬於浙江省,但是,杭州市不屬於中國。
六,概念的屬性取決於當時的語境 順便說一句,一個詞項是什麼概念,取決於當時的語境,例如: 1,“費馬大定理是很着名的數學問題”。這裡的“費馬大定理”屬於 單獨概念。 2,“費馬大定理是說n=3,4,5,...時沒有整數解”。這裡的“費馬 大定理”指集合概念。 還有,費馬大定理是無窮多個定理的集合,(n=2時叫做勾股定理) n=3時是一個定理,n=4時是一個定理,....。而不會有一個總定理,就 是說沒有一個集合概念的總定理。這是因為證實的局限性,證實只能增 加一個可信度,而不能證明整個理論的正確性。看到了康托爾的厲害了 嗎?他認為無窮是有級別的。數學只能證明最低級別的無窮。
從費馬大定理的被認可,我們看到了整個國際數學界思維混亂,數學界 群體缺乏基本的邏輯訓練,導致了數學在錯誤道路上運行。總之,重大 數學問題不能由幾個所謂“大師”說了算,必須由數學家邏輯學家語言 學家共同鑑定。
七,給安德魯懷爾斯鑑定的法爾廷斯也是錯誤的
莫德爾猜想與費馬大定理也不是等價關係,由莫德爾猜想推不出全稱 判斷的費馬大定理,所以,法爾廷斯推出特稱判斷的結論:費馬曲線
是一個特稱判斷,表現形式為:“有些A是B”。而一個數學定理要求: “一切A是B”。所以,法爾廷斯的結論不是一個定理,他的工作只是一 個有意義的探索,對於解決問題沒有任何作用。我們看到,許許多多的 錯誤結論獲得了菲爾茲獎。 為什麼法爾廷斯的結論是錯誤的? 原因是:我們首先需要知道有理點是 “有” 還是 “無”,法爾 廷斯也不知道,他是說:我也不知道有沒有這個有理點,我只能假定它 ,如果有,也是有限的。 現在明白了法爾廷斯的錯誤在哪裡嗎? 他犯了預期理由的錯誤:“假定費馬曲線存在有理點”,就是引 入了一個“加定存在”的非邏輯前提,這個錯誤使得後面的結論沒有任 何效力。 因為數學證明嚴禁引入非邏輯前提。 假定a成立,可以推出b,得到c,c與a矛盾,所以假定的a不能成立,得 到非a。 3,為什麼“假定”只能用於否定的結論,而不能用於肯定的結論? 一個對科學理論更強的邏輯制約因素是,它們是能夠被證 偽的。換一句話說,因為以後能夠被觀測作有意義的檢驗,理論一定有 被證偽的可能性。這種證偽的判據是區分科學與偽科學的一種方法。原 因在於證實的內在局限性,證實只能增加一個理論的可信度,卻不能證 明整個理論的完全正確。因為在未來的某一個時刻,總是會發現與理論 有衝突的事例。
數學不能放縱自己,數學要守規矩,數學必須自律。 最近幾十年,數論成果大爆炸,實際上是錯誤信息大爆炸,數論成果 是不會大爆炸的,因為,數論知識的產生成本是非常高的,數論存在了 2000多年,成果就是這麼一點點,以至於一個學習數論的學者都不可能 錯過任何知識。 八,結果 2016年我寫信給證明費馬大定理的團隊,其中有普林斯頓大學【數學 年刊】,肯黎貝,泰勒,牛津大學數學機構。2017年,安德魯懷爾斯 得知自己錯誤以後的照片,表情充滿憂慮。顯然,安德魯懷爾斯已經 接到消息,得知自己的錯誤,於是出現了這張充滿憂慮的照片。
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2023: | 2621.44億美國圓一句磨刀石磨菜刀磨得 | |
| 2023: | 朦朦站起來:流體力學告訴你,如何舀到 | |
| 2022: | 中國新聞事業編年紀事【92】 | |
| 2022: | 怪哉!當初美英法等國封城清零,為何沒 | |
| 2021: | 沙清:一個早期海歸的命運: 哈佛博士毀 | |
| 2020: | 洪水河隨想 | |
| 2020: | 文學門外蹭修養(中) | |
| 2019: | 卡達菲之子金錢換英國博士ZT | |