| 沐嵐:兔子的繁殖和斐波那契數列(2) |
| 送交者: 沐嵐 2016年06月29日22:50:52 於 [教育學術] 發送悄悄話 |
|
這個西洋人通過觀察和計算發現了兔子繁殖的規律,那便是假設兔子不死,那麼從第三個月開始每一個月兔子的總數都會是前兩個月數目之和,於是他得出了這樣一個數列: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368。寫成公式便是 F(n)=F(n-1)+F(n-2)(n≥2,n∈N*;F(1) = 1 )。這個以遞歸方式定義的公式便以這位西洋人的名字作為公式名,叫做“斐波那契數列”(Fibonacci Sequence), 又因之從兔子繁殖規律而來,也叫做“兔子數列”。再後來有個叫Robert Simson的蘇格蘭人證明了當項數趨於無窮時,斐波那契數列的後項與前項之比趨近黃金分割,也就是1.61803398875…,說明了斐波那契數列與黃金分割有天然的聯繫,所以又叫“黃金分割數列“)。
他的全名叫里昂納多.斐波那契(Leonardoda Fibonacc), 意大利比薩人,人稱”比薩的里昂納多”,生於公元1170(一說1175)卒於1245年(一說1250)。因為父親出任比薩商團外交使節的緣故,他曾跟隨他的父親在北非生活,從而接觸了印度和阿拉伯的數學。公元1202年27歲那年,斐波那契撰寫了著名的《算盤全書》(Liber Abacci--Book of Calculation)一書,成為第一個研究了印度和阿拉伯數學理論的歐洲人。他寫作這本書的主要目的是鼓勵歐洲人使用印度0到9的數字系統(०, १, २, ३, ४, ५, ६, ७, ८, ९ ) 而拋棄羅馬的( I,II,III, IV...),因為他發現相比於羅馬數字系統,印度-阿拉伯數字系統應用於商業和金融上具有相當強的優越性。德國人文主義作家格雷戈爾·賴施(Gregor Reisch)在他1503年出版的《哲學的珍寶》(Margarita Philosophica)一書中有一幅插圖,說明了那個時代的歐洲人對印度-阿拉伯數字的推崇:
圖中右邊的是古希臘數學家畢達哥拉斯正在用一塊計數板在計算,神情無奈,而左邊的人用印度數字計算則興高采烈,中間代表算術的女人裙子上寫滿了醒目的阿拉伯數字。 當然他最著名的貢獻還是發現了“斐波那契數列”。這個數列描述了很多自然現象和規律,特別在植物學領域。很多的植物的花瓣比如百合花,三角梅,玫瑰,菊花等都以某個斐波那契數組成。
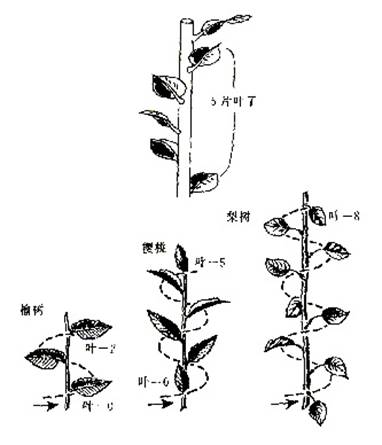
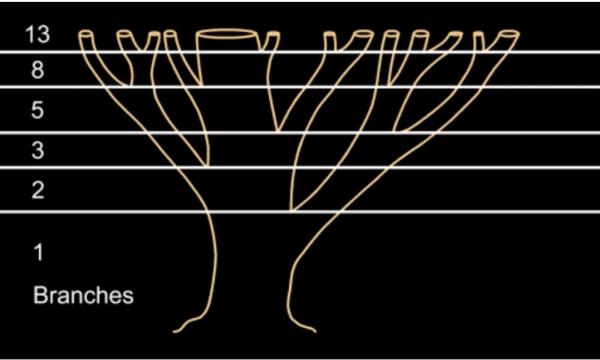
樹葉排列樹幹的生長也符合斐波那契數列的規律:
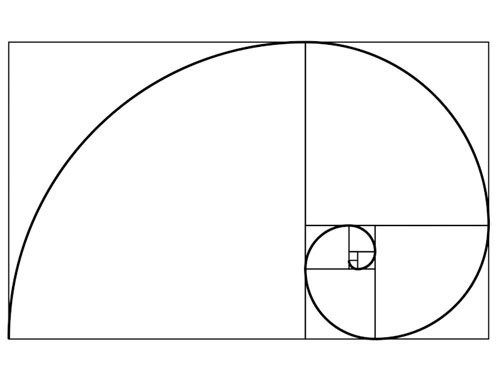
斐波那契數列在歐美可謂是盡人皆知,於是在電影這種通俗藝術中也時常出現,比如在風靡一時的《達芬奇的密碼》裡它就作為一個重要的符號和情節線索出現。 而著名的斐波那契曲線,由於它和黃金分割比例的關係,不但被古典畫家用於繪畫中,更是被今天的一些畫家作為一個繪畫門類而進行創作活動。
(待續) |
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2015: | 楊虹:在還來得及之前-----預防下一個 | |
| 2014: | 曲氏全絕律理論與曲氏龍絕律理論--中國 | |
| 2014: | 范兒522——PISA(上海):恆心與自律是成 | |
| 2013: | 隨地拉屎辯-答abc55 | |
| 2013: | 嚴重提示:孟山督針對中國的種植下家已 | |
| 2012: | bunny2:答星辰問“我是誰?” | |
| 2012: | 星辰的翅膀:與兔兄討論,人的四大關係 | |
| 2011: | 楊振寧的規範場理論是人類文明的一個里 | |
| 2011: | 泡利和楊-米爾斯場 | |