數學:應用和樂趣 (修訂版)
大部分學生不喜歡數學,覺得數學沒用,大部分數學老師也講不出數學有什麼用。一般來說,樂趣和有用連在一起,所以,家長和老師都希望找到介紹數學有用的文章。但這類文章,講數學如何的有用,舉的例子很多是二次世界大戰期間,數學家如何神武,為盟軍勝利立下汗馬功勞。二戰過去七十多年了,作者怎麼舉不出新一點的例子呢?類似的文章很多,一談到數學的好處,就是如何訓練思維,如何潛移默化,拐彎抹角講了半天,一提到應用,要麼是很難的數學,象天氣預報,要麼是很遙遠的應用,象黑洞。難道沒有簡單的數學,能夠應用到日常的生活? 有的。
大家在中學都學過對數函數,很多偉大的科學家,象玻爾茲曼,愛因斯坦,申農,用這個簡單的函數做出了重大的科學突破。在這裡,我們用對數函數定義物品的價值。物品的價值定義為
-logbP
其中 P 為物品的稀缺程度,範圍從 0 到 1, 0 為極度稀缺, 1 為無限豐富,b 為這個物品的生產廠家數目。我們來看一下這個函數的性質。
首先,一種物品的價值是稀缺程度的遞增函數,物品越豐富,其價值越低,如果這種物品無限豐富,也就是P = 1,其價值為零。比如說,空氣對我們非常重要,幾分鐘不呼吸,我們就活不下去。但由於空氣無處不在,其經濟價值為零。下圖是價值與稀缺程度之間的關係。
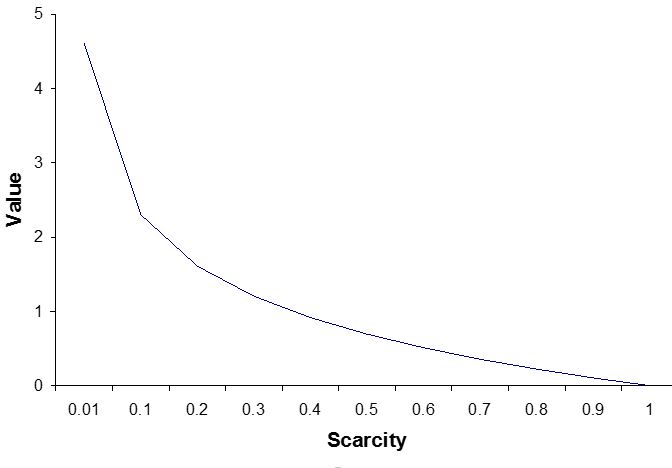
很多人把經濟價值等同於對社會的貢獻。當今糧價很低,很多人認為農民對社會的貢獻低。但如果糧食太貴,有人買不起,很快引發社會動亂。所以很多國家的政府採取各種政策,以保證糧食的充足,同時也造成糧價低廉。很多政府為了保護農民利益,大量補貼農民。從這個價值理論,我們可以清楚看到,經濟價值不等同於對社會的貢獻。
我們再來分析生產廠家的個數對價值的影響。b 越小,物品的價值越高,下圖是物品的價值與生產廠家數目的關係。一樣物品,生產的廠家越少,價值越高,大家都知道壟斷和寡頭經營的行業,利潤很高。這個分析不僅可以應用到產品上,也可以應用到任何社會系統,世界上影響力大的宗教,象猶太教,基督教,伊斯蘭教,大多是一神教,而佛教和大多數早期的宗教,是多神教,一神教對教徒的控制能力比多神教強很多,當一神教碰到多神教的社會,往往會擊敗對方。很多職業收入高,往往是由於這些職業由唯一的組織代表。比如說,加拿大所有的醫生,都屬於同一個醫學學會,沒有任何競爭;加拿大醫生的收費,是統一的,也沒有任何競爭;病人看病,必須通過唯一的家庭醫生,彼此之間沒有競爭。這就是為什麼加拿大醫生的地位,比中國高很多。我們經常說西方經濟是自由競爭的市場經濟,但其中最重要的部門,象醫療,教育,軍工,以及龐大的政府本身,都由工會和壟斷機構控制,很少自由競爭。
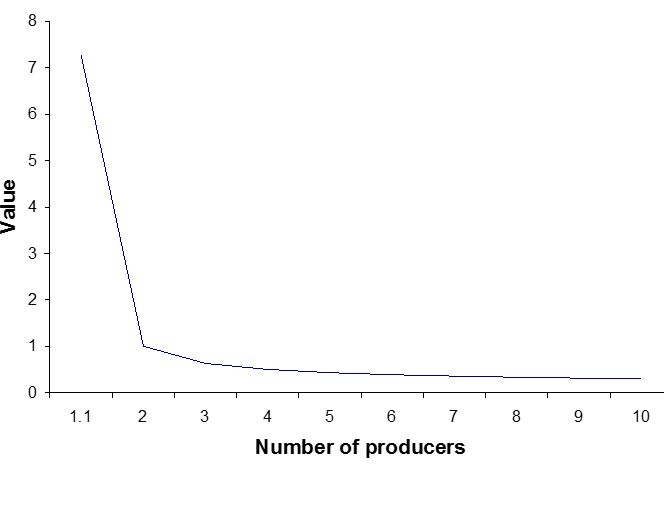
減少選擇,對增加價值有決定性的影響。所以幾乎所有經濟,政治活動,都以減少競爭,增加壟斷權力為目的。我們常說的專利法和知識產權保護就是一個例子,知識產權保護最常用的理論是鼓勵創新,但創新最多,給消費者帶來最多利益的行業,象信息技術,往往是知識產權最自由的行業,而知識產權保護最嚴格的行業,象生物醫學,往往是納稅人花大錢,消費者受益甚少的行業。最近, 很多人討論無效疫苗和有毒疫苗的問題。疫苗的採用是由政府決定的,由於政府是最強勢的壟斷機構,這類事情的產生是必然的。
從上面的討論,我們看到,一個簡簡單單的對數公式,可以幫助我們深刻了解這個社會中形形色色的活動。很多原本不喜歡數學的學生,也很開心學到對數函數的各種性質。關於這個公式更多的應用,可參看我的文章:價值的熵理論。
An Entropy Theory of Value: Forthcoming in Structural Change and Economic Dynamics
https://www.researchgate.net/publication/228398386_An_Entropy_Theory_of_Value










