| 數學及其應用 |
| 送交者: jingchen 2018年12月26日08:16:10 於 [教育學術] 發送悄悄話 |
|
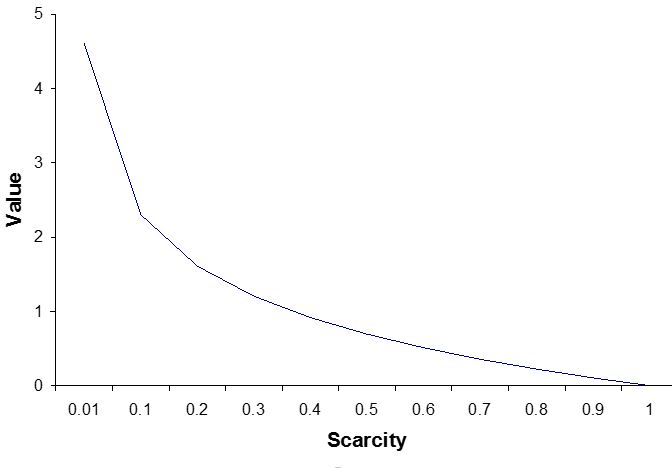
數學及其應用 幾乎所有的數學都源於應用問題,但時代久遠之後,人們往往忘掉了。比如說,幾何學,是一門純數學,但幾何學 (geometry) 的意思是測地學,顯然源於應用問題。對應用問題的理解,很大程度上決定了數學和科學的發展方向。下面我們用拓撲和分析在經濟學領域的應用來分析一下。 很多人都看過一本叫做《美麗心靈》的書,或者根據此書改編的電影。此書的主人公叫納什,他建立了博奕論中一個重要的結果,用的是拓撲學的方法。主流經濟學理論的基礎是一般平衡態理論,其嚴格的數學證明,也是建立在拓撲學基礎上的。可以說,拓撲學為主流經濟學理論提供了嚴格的數學基礎,但這是不是一個合適的基礎?經濟問題是數字問題,一件貨物,如果成本是100塊錢,賣了110塊錢,就能盈利,賣了90塊錢,就會虧本。但是從拓撲學角度,90 ,100 ,110是沒有區別的,所以拓撲學不能表達經濟學和生物學中最根本的特徵,追求非負的投資回報率。可是由於拓撲學理論簡單,早期的數理模型往往源於拓撲學。 價值理論是經濟學理論的基礎。主流經濟學價值理論叫做Arrow-Debreu 理論[1], 為此Arrow 和 Debreu兩人都拿了諾貝爾獎。這個理論也是採用拓撲學方法,不能提供一個定量的分析。而對數函數的方法則對決定經濟價值的因素提供了清晰的分析。我們來具體了解一下。 在一個新的價值理論里 [2], 物品的價值定義為 -logbP 其中 P 為物品的稀缺程度,範圍從 0 到 1, 0 為極度稀缺, 1 為無限豐富,b 為這個物品的生產廠家數目。我們來看一下這個函數的性質。
首先,一種物品的價值是稀缺程度的遞增函數,物品越豐富,其價值越低,如果這種物品無限豐富,也就是P = 1,其價值為零。比如說,空氣對我們非常重要,幾分鐘不呼吸,我們就活不下去。但由於空氣無處不在,其經濟價值為零。下圖是價值與稀缺程度之間的關係。
很多人把經濟價值等同於對社會的貢獻。當今糧價很低,很多人認為農民對社會的貢獻低。但如果糧食太貴,有人買不起,很快引發社會動亂。所以很多國家的政府採取各種政策,以保證糧食的充足,同時也造成糧價低廉。很多政府為了保護農民利益,大量補貼農民。從這個價值理論,我們可以清楚看到,經濟價值不等同於對社會的貢獻。
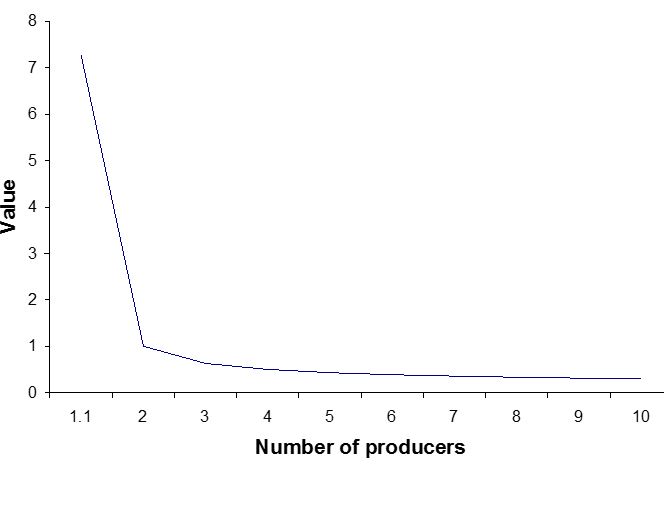
我們再來分析生產廠家的個數對價值的影響。b 越小,物品的價值越高,下圖是物品的價值與生產廠家數目的關係。一樣物品,生產的廠家越少,價值越高,大家都知道壟斷和寡頭經營的行業,利潤很高。這個分析不僅可以應用到產品上,也可以應用到任何社會系統,世界上影響力大的宗教,象猶太教,基督教,伊斯蘭教,大多是一神教,而佛教和大多數早期的宗教,是多神教,一神教對教徒的控制能力比多神教強很多,當一神教碰到多神教的社會,往往會擊敗對方。很多職業收入高,往往是由於這些職業由唯一的組織代表。比如說,加拿大所有的醫生,都屬於同一個醫學學會,沒有任何競爭;加拿大醫生的收費,是統一的,也沒有任何競爭;病人看病,必須通過唯一的家庭醫生,彼此之間沒有競爭。這就是為什麼加拿大醫生的地位,比中國高很多。我們經常說西方經濟是自由競爭的市場經濟,但其中最重要的部門,象醫療,教育,軍工,以及龐大的政府本身,都由工會和壟斷機構控制,很少自由競爭。
減少選擇,對增加價值有決定性的影響。所以幾乎所有經濟,政治活動,都以減少競爭,增加壟斷權力為目的。我們常說的專利法和知識產權保護就是一個例子,知識產權保護最常用的理論是鼓勵創新,但創新最多,給消費者帶來最多利益的行業,象信息技術,往往是知識產權最自由的行業,而知識產權保護最嚴格的行業,象生物醫學,往往是納稅人花大錢,消費者受益甚少的行業。
從上面的討論,我們看到,一個簡簡單單的對數公式,可以幫助我們深刻了解這個社會中形形色色的活動。很多原本不喜歡數學的學生,也很開心學到對數函數的各種性質。關於這個公式更多的應用,可參看價值的熵理論[2]。 經濟學的拓撲理論最初建立於半個多世紀之前,這些早期的探索者值得我們尊敬,但是,拓撲學理論沒有能夠把實際經濟活動中重要的因素表達出來,而分析理論則可以。 拓撲學理論是數學的主流,另一門數學的主流是代數幾何。代數幾何是關於多項式函數的幾何理論,多項式自然古老,多項式自然重要。但大多數重要的物理問題,生物問題和社會問題包含指數函數和對數函數,所以代數幾何的研究不涉及很多自然界最基本的問題。
我們很多人對數學的現狀,科學的現狀,經濟學的現狀不滿意。但是要改變這種狀況,需要我們的積極參與,把好的數學方法引入經濟學研究,把重要的經濟學問題引入數學研究。只有這樣,數學這棵老樹,才能開出絢爛的新花。 具體一點,我們用電磁波譜作一個比喻,從無線電波到伽馬射線,但是給人們帶來最多信息的是人們熟悉的可見光。同樣,從拓撲學到代數幾何,數學方法從一般到具體,拓撲學太一般了,生命科學和經濟學中所需要的定量化往往不能表達,而代數幾何限制過多了,生命科學和經濟學中最常出現的對數函數和指數函數被排除在外。我們最需要的是普通的分析理論,就像我們在日常生活中,最需要的是普通的可見光一樣。
參考文獻 1. Debreu, G. (1959). Theory of value; an axiomatic analysis of economic equilibrium. New York: Wiley. 2. An Entropy Theory of Value: Forthcoming in Structural Change and Economic Dynamics https://www.researchgate.net/publication/228398386_An_Entropy_Theory_of_Value 下面是一篇關於數學及其在社會科學中的應用的通俗介紹。數學及其在社會科學中的應用 |
|
 | |
|
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2017: | Introduction to Instancology-1 | |
| 2017: | Introduction to Instancology -1 | |
| 2016: | 再見驢十八:我讀書多你不要欺負我 ( | |
| 2016: | 子貢尊師 | |
| 2015: | 破舢板當海盜船成功只為騙你 | |
| 2014: | D.QU:平水韻入聲十七韻部歸入中華新韻 | |
| 2013: | 毛澤東 - 中國文化“二面派價值觀”的 | |
| 2013: | 老Q&皮膚&慌大夫,關於GMO食物導致癌症 | |