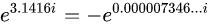| 四色定理、哥德巴赫猜想、費馬大定理、黎曼猜想、歐拉公式融入超 |
| 送交者: wxmwrkhp 2019年01月16日17:26:49 於 [教育學術] 發送悄悄話 |
|
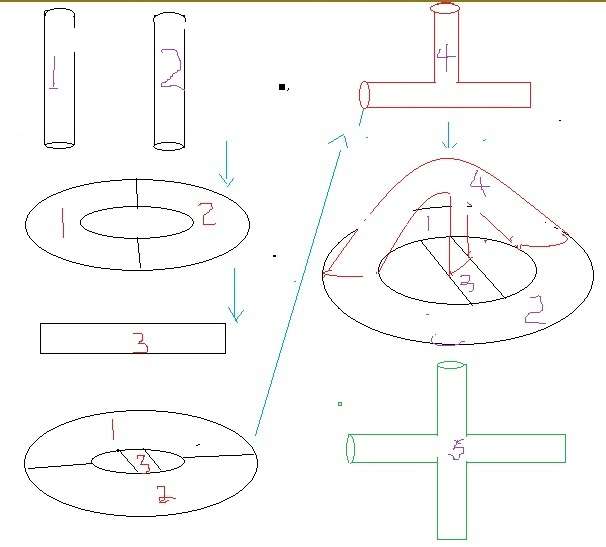
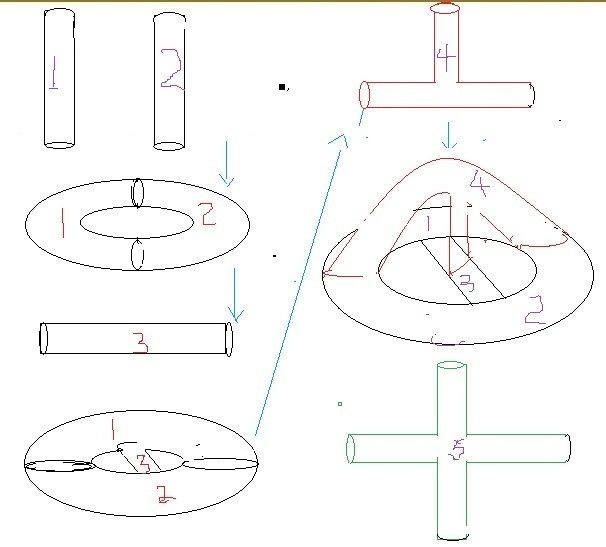
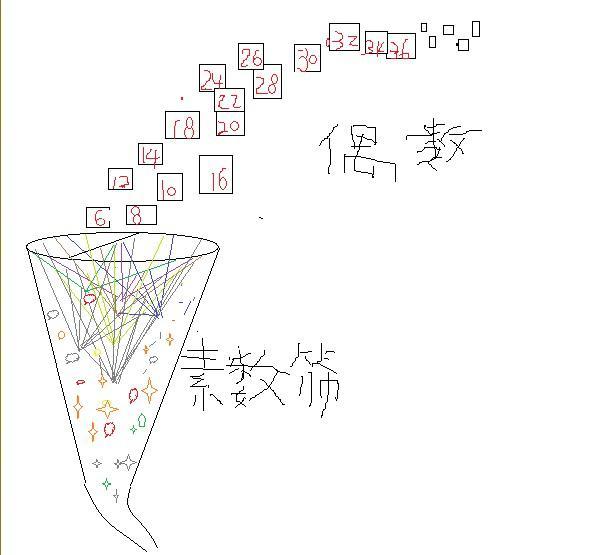
哥德巴赫猜想、費馬大定理、黎曼猜想、歐拉公式、m理論大融合62 人贊了該文章 一,前言 大自然的運行有兩種模式,一種是由一到多,例如樹木由一根主幹生長到很多樹枝樹葉,人類祖先最開始只有亞當和夏娃再到數千人到現在70億;另一種是由多到一,例如千萬的山間小溪匯集江河最後到海,再一個就是人類的知識,由多學科多門類融合到一個總理論。 科學最讓人不可思議的是它的融合,無數自然現象可以歸結為物理學、化學、生物學、....。 今天的文章註定是一個載入史冊,它是人類思維的輝煌壯舉,它把數學中最經典的哥德巴赫猜想、費馬大定理、黎曼猜想、歐拉公式和廣義相對論量子理論的m理論融合在一個模型里。 二,從四色定理開始 法蘭西斯·古德里於1831年生於倫敦,在1852年提出的猜想,只需要四種顏色為地圖着色。這是因為他發現在平面上或者球面上,只能有4個區域兩兩相連,英國數學家德摩根證明了平面上不存在5個區域兩兩相連。 1974年德國的林格和美國的楊斯證明了在曲面上染色定理,例如,在一個汽車輪胎形狀的環面需要7種顏色,因為可以構造7個兩兩相連的區域,6種顏色肯定不夠的;在有兩個洞的雙環面需要8種顏色,因為可以構造8個兩兩相連的區域,7種顏色肯定不夠的;....。 三,數學家證明了可以構造無窮多個兩兩相連的區域 如果你不能理解,讓我慢慢道來: 現在有兩根管子,一個記為1,一個記為2,它們代表兩個區域。我們假定所有的管子都是可以隨意拉伸和彎曲的。 把兩根管子端端相連,就是一個汽車輪胎一樣的環,它有兩個區域,我們再用一根直管子記為3,安在這個環的中間,一頭連着區域1,一頭連着區域2,現在它是有兩個洞的雙環了,有三個區域兩兩相連。 現在我們用一個“丁”字型的三叉管,記為區域4,三個端口分別與區域1,區域2,區域3 相連。於是現在有4個區域兩兩相連; 我們再用一根四叉管記為區域5,4個端口分別與區域1,2,3,4相連,現在有5個區域兩兩相連。 這個步驟可以無限制進行下去,用五叉管,六叉管,...。構造無窮多個區域,它們都是兩兩相連的。 數學家和物理學家把這個叫做岐管。
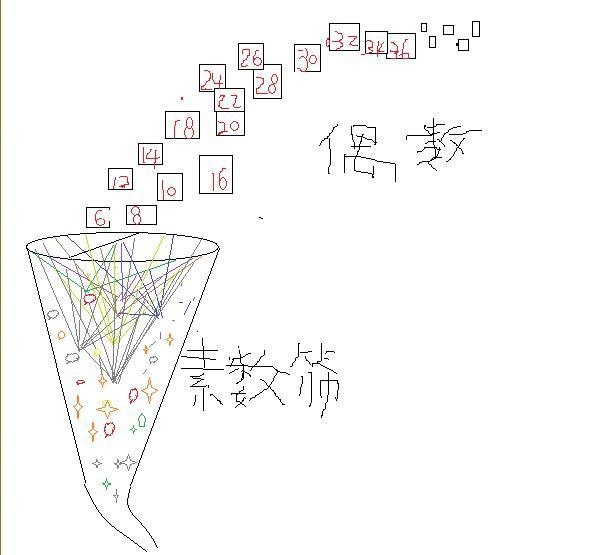
四,數論與圖論聯繫起來 在數論中,最重要的元素就是素數,歐幾里得證明了有無窮多個素數,並且它們有一個特點就是兩兩互素。無窮多個兩兩互素的素數與無窮多個兩兩相連區域一一對應。 就是說用這個方法把數論與圖論聯繫起來,這個方法的意圖叫做朗蘭茲綱領。 區域1,代表第一個素數2,第二個區域代表第二個素數3,...,第n個區域代表第n個素數。 我們把這個岐管倒過來,就像一個網子,籃球網子。籃球網子是把籃球往裡面投。 公元前300年古希臘有一個數學家叫做埃拉特斯特尼,他把這個網子當成篩子,把自然數往裡面扔,他說凡是合數通過篩子以後就會從網子裡面篩掉,留下的是素數,這個就是著名的埃拉特斯特尼篩法。
五,與哥德巴赫猜想聯繫起來 我們上面這個岐管篩子是把偶數往裡面扔,哥德巴赫說,大於4的偶數一個也不會漏出篩子,除了6=3+3以外,其他偶數都是可以在不同的素數區域被攔截。例如8會在區域2也就是素數3和素數5(第三個區域)被攔截;偶數10會在素數3和素數7的兩個區域之間被攔截;...。總之,無窮多個偶數都逃不脫這個網子,沒有一個偶數可以漏到外面去。 六,哥德巴赫猜想與費馬大定理聯繫起來了 看到沒有?數論與圖論已經融合一起了。 這個還不算神奇,這個岐管的內部空間我們記為X,外部空間記為Y,它有很多洞,可以有無窮多個洞,可以有無窮多個空間維度n,宇宙內外整體記為1,就是說 Xⁿ+Yⁿ=1,這個叫做費馬曲線,它是由費馬大定理Aⁿ+Bⁿ=Cⁿ同時除以Cⁿ得到的。 費馬大定理與哥德巴赫猜想聯繫起來了。 七,這個岐管就是m理論的架構 物理學家認為,宇宙是10維空間或者11維空間,或者26維空間等5個版本。還有物理學家認為有無窮多個維度的空間。他們管這個理論叫做玄理論或者M理論,是把廣義相對論與量子理論結合一起的終極理論,霍金說是最後的理論。 八,與黎曼猜想聯繫起來了 數學家考慮的是怎樣計算這個岐管上的區域或者計算區域上面的一個點。如果岐管上某一個區域 n,在n上的一個點是1/n,因為這個岐管有無窮多個維度,或者很多維度,我們要定位這個點,就要考慮它的管壁——實部,還有考慮它的內外空間位置——虛部。 所以,這個點
,S=α+βi。 i是虛數,α表示實部,實部當然是1/2,因為這個多維宇宙等於1,岐管屬於實部,實部上的點當然是1/2。這個正是黎曼函數黎曼猜想
。物理學裡,真空是能量的“零點”。 黎曼猜想與物理學和費馬大定理聯繫起來了。 九,與歐拉公式聯繫起來了 虛部怎麼計算呢?岐管內部看成一個圓管,在岐管上的一個點1/K^S,做一個截面,就是一個圓。大家知道歐拉公式嗎?
以e^0=1開始,以相對速度π,走了i時間(參見百度百科“虛時間”),再加1,回到原點。
我們設岐管上的點1/K^S為Δ,那麼,e^Δi=-1。 包含了時間(時間有虛的涵義)和空間。 虛時間是為了對應時間起點(大爆炸)而定義的一個概念。在虛時間這個概念體系裡,在比三維更高的維度空間,時間並不是一條直線,而是一個閉合的圓,沒有起始也沒有終結,宇宙的起點如果源自大爆炸,那在此之前的時間將無法定義。因此,為了解決奇點之前時間應該如何,我們引用到了複數的概念。 如果走過頭,假如超過了π,走到了3.1416,讓我們看一下會發生什麼情況: 因為π=3.141592653,所以(1)式:
因為圓周率: π=3.141592653...=3.1416-0.000007346。 所以 (2)式為:
公式(3)可以寫成:
我們知道,同底數相除,指數相減 ,反過來也一樣,即同底數指數相減,就是兩個數相除 公式(4)可以寫成:
.........(5) 當大於π時,就是時間走過頭了,落入第三象限。歐拉公式是將指數函數e^πi解析延拓到整個複平面上。虛時間就是——(5)式物理學中出現這種情況: 不同時代的人在一個特殊的空間相會,例如今天的人(e^3.1416i)與3000年前的人-e^0.000007346相遇(或者今天的人與未來的人相遇):拿着長矛大刀的古人在與駕駛航空母艦和f—35的帶着核彈頭的現代人相遇,誰怕誰? 歐拉公式在2011年被評為世界上最美的10個公式之首。 我們的宇宙是由數學最經典的問題和物理學最經典的問題組成的。 與愛因斯坦質能公式聯繫起來 玄理論認為,從更加宏觀角度看,比如億萬年,我們的宇宙就像在一張紙一樣薄的膜片上或者肥皂泡膜上,光無法逃逸出膜,被限制在膜上,但是引力可以穿越宇宙的膜向外傳播,玄理論的科學假設,宇宙所有的粒子都被局限在一個四維膜的宇宙中,而膜宇宙漂浮在更高維度的體宇宙里,不過,幾種特殊的粒子可以從膜宇宙中穿出,其中,最出眾的就是引力和惰性中微子。 上面的膜宇宙,對於膜,是一種沒有厚度的東西,但是有一個曲面,這是有面積的,設為c,膜包含了質量和能量。E=mc^2。愛因斯坦方程中式中E為能量,m為質量,c為光速。它是一切物質運動速度的最大極限。這個公式就是愛因斯坦質能方程式。在膜宇宙中,光速只能繞着膜運行,膜的表面積就是光速掃過的面積。因此,c^2=E/m。 我們把愛因斯坦方程也引進了。我們生活在費馬大定理的宇宙空間,出面旅行(宏觀)需要黎曼猜想和歐拉公式計算路程,穿過哥德巴赫猜想的蟲洞,才能到達彼岸。 我們生活在高維宇宙的一小片中,大到銀河宇宙,小至原子夸克,都是 弦線構成的。 |
|
 | ||||||||
|
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2018: | 參加香港《主權在民》的民主選舉真爽, | |
| 2018: | 關於我們的認知判斷 | |
| 2017: | 歷史的必然性看葉公好龍 | |
| 2017: | 彭運生:文化沉思錄(9) | |
| 2016: | 溪谷閒人:美國簡史十二.棉花是國王 | |
| 2016: | 大喜事:證明了假共“讓利台灣”以金錢 | |
| 2014: | 初等教育的怪胎﹕高考最牛班 | |
| 2014: | 七律:無題(新韻) | |






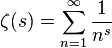
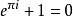
 ......(1)。
......(1)。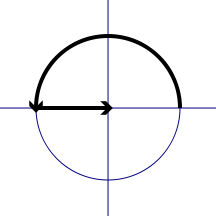

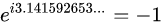
 .......(2)
.......(2)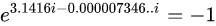
 .......(3)
.......(3)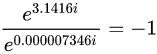
 ........(4)
........(4)