| 767、托爾斯泰主義;莫比烏斯帶;拓撲結構 廣相論17 |
| 送交者: 和顏清心 2019年05月19日13:07:14 於 [教育學術] 發送悄悄話 |
|
� 5分鐘�
2分鐘 �
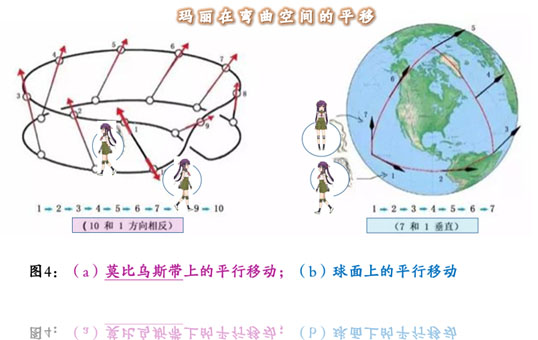
� 假如將瑪麗面對的方向用一個箭頭(矢量或曰向量)來表示, 上圖左邊所示的是一個矢量在莫比烏斯* 帶上的平行移動, 當矢量從位置1出發,沿着數字1、2、3……一直移動到10, 也就是回到原來的出發位置時,得到的矢量與原來的反向。 而上圖右邊所示的是球面上的平行移動, 當矢量從位置1出發,沿着數字1、2、3……一直移動到7, 也就是回到原來的出發位置時, 得到的矢量和原來的矢量形成垂直方向。 *莫比烏斯帶,是一種只有一個面(一個表面) 和一條邊界的曲面,也是一種拓撲結構*。 它是由德國莫比烏斯和李斯丁在1858年獨立發現的。 這個結構可以用一個紙帶,旋轉半圈, 再把兩端粘上後,輕而易舉地製作出來。 【說明】 在數學上,球面上一個向量*, 沿着‘閉環路’平行移動。 這個向量所轉過的角度α ( 阿爾法) , 與閉環路內部的面積——成比例。 *向量(也稱矢量),指具有大小和方向的量。 它可以形象化地表示為帶箭頭的線段。 箭頭所指:代表向量的方向; 線段長度:代表向量的大小。 與向量對應的量叫做數量(物理學中稱標量), 數量(或標量)只有大小,沒有方向。《百科資料》 通常人們所理解的平行線不是非歐幾何概念的。 歐幾里得幾何是平面幾何, 所說的平行線是相對平面而言的, 而非歐幾何中的平行線是相對曲面而言的。 為什麼曲面幾何中 “過(所謂)直線外一點, 連一條平行線也引不出來”? 這得拿地球儀做參考, 因為球面是彎曲的, 球面上兩點之間的最短距離是大圓周—— 用球面上的兩點和球心三點做一個平面, 截出的那個圓周就是大圓周 (大圓周也叫短程線)。 黎氏幾何中的短程線, 就類似於歐氏幾何(平面幾何)中的直線。 �
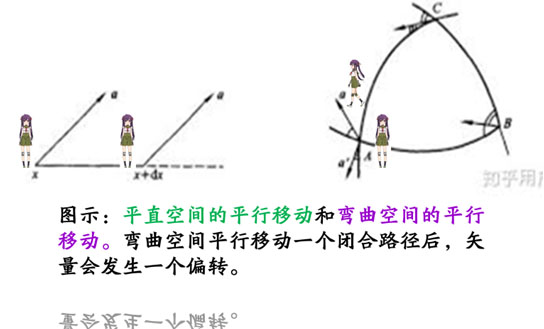
� 【圖示】平直空間的平行移動和彎曲空間的平行移動 在彎曲空間,平行移動一個閉合路徑後,會發生偏轉。 上面兩個例子說明, 在曲面上平移一圈兒後,不能保持原來的方向, 而是出現與出發時的方向有偏差的情況。 這個偏差與曲面的‘曲率’有關, 反映了曲面的彎曲程度。 � 3分鐘 拓撲是研究幾何圖形或空間在連續改變形狀後還能保持不變性質的一個學科。它只考慮物體間的位置關係而不考慮它們的形狀和大小。 謝謝。 |
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2018: | 唐映紅| 監控學生的智慧校園--就為培養 | |
| 2018: | 震撼: 從北大到耶魯。。。 | |
| 2017: | 259 世上講修行的事多了去了 | |
| 2017: | 增智健體活動階段性小結-亻財材才徵召- | |
| 2014: | GEORGES 等著:漢詩從二絕律到九絕律-- | |
| 2014: | 范兒506——「我的名片」:恆心與自律 | |