| 781、絕境下的人性·廣相論24(曲面微分幾何) |
| 送交者: 和顏清心 2019年06月21日06:59:27 於 [教育學術] 發送悄悄話 |
|
《絕境下人性的極致》
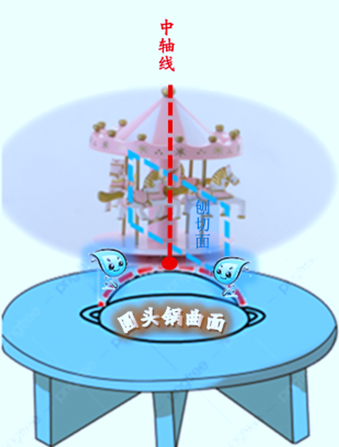
……河水咆哮着,沒有過河的筏子, 只有幾隻黑子父親自製的葫蘆可以幫助渡河。 歐文緊緊抱着年幼的花花, 又用繩子捆着受傷的安潔, 三個人艱難地在水中游着, 安潔不會游泳,又因傷勢過重, 已經沒有力氣,配合歐文往前游了, 安潔看着極度疲勞的歐文, 看到歐文正在拼力地拖着自己往前游, 她本能地拿出匕首割斷繩子, 在割繩子的瞬間,她的眼淚流下來……, 她在向歐文告別, 她在祝福歐文平安脫離險境……。 安潔本可以選擇不割繩索, 是怎樣的勇氣、怎樣的愛, 能讓一個人在那一瞬 斷然放棄生命成全他人? 為了不拖累歐文, 她把纏繞在身上的繩索切斷, 滔滔河水淹沒了她的身軀, 沒有一句豪言壯語, 有的只是默默的奉獻, 而這一奉獻, 正為天地譜寫了一曲高尚靈魂的讚歌! 安潔,你是一位天使。 開心(曲面)微分幾何 (曲面)微分幾何過於抽象, 對初學者來說,如果不詳加解釋, 形同虛設、等於沒學, 這就有點些像我們來到一個國家, 國內所有情景異常枯燥,毫無生氣, 除非不得己, 一個正常人是無法在這裡活下來的。 話說數學家是如何將彎曲時空的曲率 用到曲面微分幾何的呢?下面舉例說明。 先看一個栗子,我們知道, 對於曲面上某個切點G, 通過旋轉(像旋轉木馬那樣) 可以形成無限多面 (由於紙面限制,圖中只出現一個面)。
每個木馬經過旋轉,可以形成相應的 無限多切面*和無限多切線*。 【注釋】 ‘切面’有球切面、圓柱切面和圓錐切面。 下面先解釋一下什麼叫‘球切面’ 以及什麼是‘切點’和‘切線’。 (1)與球面只有一個交點的平面叫‘球切面’。 (2) 球與切面的公共點叫‘切點’。 (3)和球只有一個公共點的直線,叫‘球的切線’。
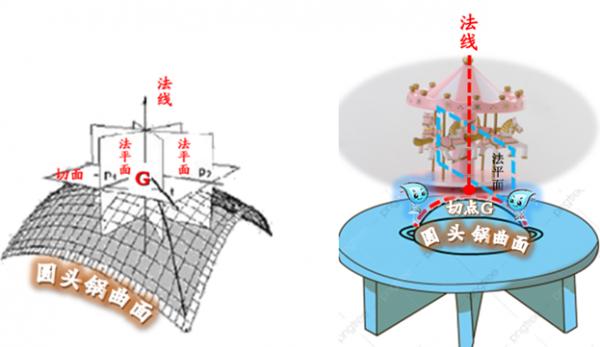
這些切線如果是在‘一個平面’上 (該平面是處在與旋轉空間的 ‘豎直線’成90度的位置上), 按照相關定義, 我們稱‘這個平面’是這個點的‘切平面’。 傻了吧?再讀一遍。再讀一遍,仍模糊……, 好了,現在讓我們想象有一座 旋轉木馬, 建築商(異想天開地)將這旋轉木馬, 建在一個山包上…… 嘿,等一下,遊樂場建在山包上? 誰還敢去啊?那麼就換一下, 讓我們想象,旋轉木馬是用生日蛋糕做成的, � 我們可以把它放在一個‘倒扣’的圓鍋上, 然後用小刀,把這個蛋糕,從‘中軸線’處, 切成許多份兒,於是會看到每一份兒 都出現了蛋糕的切面, 這種切面也可稱‘刨切面’ (如圖),
細看這個蛋糕有個特點, 就是它比普通蛋糕含水量多(即鬆軟許多), 蛋糕含有許多水分, 這時如果有個精靈利用魔法, 將蛋糕的水份聚集起來, 那麼被聚集的水份, 就會像小瀑布似地 緊貼着圓鍋鼓鼓的立體曲面往下流淌(如下圖)
待續。謝謝。 |
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2018: | 漢武帝的真正貢獻是反封建復辟 | |
| 2018: | 對網友老幾博 “兔子的範例簡介”的簡 | |
| 2017: | 活着如何做一個不是惡霸的大地主 (六 | |
| 2017: | 彭運生談藝錄(64) | |
| 2016: | 天下網商前執行主編財經記者胡采苹被曝 | |
| 2016: | 現代城市需要一些湖泊 | |
| 2015: | 範例哲學對量子纏繞現象的解釋 | |
| 2015: | 中國現代哲學家學會:再談範例的分類 | |