| 微積分之後的數學危機 |
| 送交者: 天蓉 2022年03月24日13:39:35 於 [教育學術] 發送悄悄話 |
初等數學的研究對象是不變的量,而高等數學的研究對象則是變量。這句話本身平淡無奇,卻道出了初等數學與高等數學的根本區別,也就是微積分之前和之後的數學之區別。微積分的誕生可以說,如果沒有微積分,就沒有現代科技。微積分誕生的歷史源遠流長,但最後一步是由牛頓和萊布尼茲完成的。兩人的微積分風格不同,貢獻各異。牛頓最大的貢獻是把微積分用於物理上,構思了牛頓三大定律及萬有引力定律。並用微積分方法,討論了潮汐、歲差等現象。 萊布尼茲最主要的貢獻是對概念、方法、技巧等清楚的梳理,加上符號的運用。這些符號受到人們的喜愛,一直使用至今。 1665年,牛頓從劍橋大學為了躲避瘟疫回到了鄉下老家,蘋果樹下的思考萌生了萬有引力定律。這是家喻戶曉的故事,那年他才22歲。那段時間除了研究引力之外牛頓還發明了微積分,後者對科學之意義不下於前者。 牛頓考慮微積分是為了解決動力學問題,即運動中物理量與時間的關係問題。他把這種數學理論叫做“ 流數術 ” ,實際上就是現代說的微積分。那年的5月20日,牛頓第一次在他的手稿上描述他的“流數術”,後人便把這一天作為微積分的誕生日。 牛頓將一切基本變量叫做“流量”(用x、y、z表示),而將流量隨時間的變化率,即速度等,稱之為“流數”。流數用x、y、z上面加一點(或者x’,y’,z’)來表示。 牛頓“流數術”要解決兩類問題: (1)已知流量間的關係,求流數的關係,這相當於微分學。 (2)已知流數間的關係,求流量的關係,相當於積分,問題(1)的逆問題。 使用現在的微積分語言,牛頓的“流量”即變量,“流數”即導數。 如何計算流量和流數?牛頓從二項式展開成無窮級數的問題開始思考,並由此對“無窮”的概念有所突破。為此目的,牛頓定義了一個時間的無限小瞬“o”,作為流數術的基礎。這個無限小的時間瞬將引起流量的瞬,由此便能計算流數,即兩個“瞬”的比值。 例:兩個流量:x和y,隨時間t變化並有如下關係:x3 + xy + y3 = 0 (1) 無限小時間瞬o將引起兩個流量的無限小瞬,分別記為x’o, y’o。 在公式(1)中分別用x+x’o, y+y’o代替x和y,再減去(1)得到: 隨時間變化的流量x和y,有如下關係:x3 + xy + y3 = 0 (1) 無限小時間瞬o將引起兩個流量的無限小瞬,分別記為x’o, y’o。 在(1)中用x+x’o, y+y’o代替x和y,再減去(1)得到: 3x2x’o+3x(x’o)2+(x’o)3+xy’o+x’oy+x’y’o2+3y2y’o+3y(y’o)2+(y’o)3 = 0 兩邊同時除以o:3x2x’+3x(x’)2o+(x’)3o2+xy’+x’y+x’y’o+3y2y’+3y(y’)2o+(y’)3o2 = 0 然後令o= 0:3x2x’+xy’+x’y +3y2y’= 0 整理得x’和y’的關係:x’/y’ = -(3y2+x)/( 3x2+ y) 牛頓發明了微積分,並用微積分的語言寫下了牛頓三大定律和萬有引力定律。以及後人又在微積分的基礎上建立了數學物理方程、黎曼幾何等數學分支。這些數學理論,不僅幫助牛頓和麥克斯韋等人,建立了宏偉輝煌的經典力學和經典電磁理論,並且推動了理論物理中量子力學、相對論、混沌理論等數次革命。回顧其間的這段漫長的歷史過程,是既耐人尋味,又發人深思的。 牛頓像是個上帝派來的魔法師,他右手點亮經典力學之火,左手握着微積分,數學和物理的殿堂從此有了光明。有位英國詩人為牛頓寫下了令人感動的墓志銘:"上帝說,讓牛頓降生吧。於是世界一片光明。"牛頓點亮了科學的火把,照亮世界,給人類帶來光明。 當年牛頓與萊布尼茨的微積分發明權產生爭論,兩人都是小肚雞腸。並且,還將兩人所在國家的國家榮耀、民族情緒牽扯其中。將兩位科學家的個人之爭,演變成了英國科學界與德國科學界、乃至與整個歐洲大陸科學界的對抗。英國數學家不願意接受萊布尼茨更為好用的符號系統,而要堅持使用牛頓的,實際上影響了英國數學研究的發展。 牛頓和萊布尼茨的微積分都不夠嚴謹,之後被歐拉、拉格朗日、拉普拉斯、達朗貝爾等人精雕細刻,才系統化和嚴密化為後來的樣子 微積分的危機
所謂的數學危機,實際上並不是什麼危機,不過是在數學發展過程中幾個關鍵的時間點而已。在這些時間點,人們對數學中的概念發生了質的變化。因此,解決危機的辦法就是首先需要接受新概念,然後用數學的語言和規範嚴格地完整和理清這些概念。 例如,發生於古希臘的那次危機,其實什麼危機也沒有,只不過因為畢達哥拉斯學派原來對數的認識是不足夠不完善的,數不能僅僅被理解為m/n的有理數形態,還需要擴展到無理數。因此,人們首先需要接受無理數這個新概念,然後,數學家創立了新的比例論、完善了窮竭法,將無理數概念統一到“數”的領域中,因而克服了所謂的“危機”。 牛頓和萊布尼茨創建的微積分,解決了許多實際問題,例如,微積分解決了力學中的速度變化問題,它馳騁在近代和現代科學技術前沿,建立了數不清的豐功偉績,但也招來不少質疑的聲音。 最主要又嚴峻的質疑,來自於一位教區主教George Berkeley。不要以為伯克利只是一個神學人士,有人說他是因為憎恨科學捍衛宗教而攻擊牛頓,其實不完全如此,捍衛宗教固然是其目的之一,但未必是“攻擊”,因為他的確抓住了當時牛頓(或萊布尼茨)微積分的要害:不嚴密! 看看伯克利何許人也。你可能沒聽過他,但你可能聽過美國加州有所叫伯克利的大學!沒錯,這座大學就是以他而命名的,因為他熱衷教育事業,為紀念他對教育做出的貢獻。除了是教育家之外,他有眾多的身份:英國著名的主觀唯心主義哲學家、嚴肅的數學家、他關心大眾生活,為人民謀福利,還被當時的人稱為“善的主教”。 1734年,牛頓過世7年後,伯克利出版了分析學家一書挑戰微積分: “親愛的牛頓,請你誠懇地告訴我,如果你還殘存對信仰的敬畏。你那自鳴得意的“瞬”,究竟是何方神聖?它飄然而來,因為要作你的分母;它離奇而逝,因為要成全你的流數。你不需要它,就判處它死刑;你需要它,又召喚出它的亡靈。” 無窮小“瞬”,究竟是何方神聖?飄然而來又離奇而逝,零或非零, 消失量之幽靈? 貝克萊對牛頓所闡述的“無窮小”提出質疑,並非無理取鬧。因為牛頓無窮小定義的導數並不嚴密,即使沒有貝克萊提出質疑,最後也會有人提出無窮小概念的問題。當時的微積分仍然受希臘幾何的影響,還處於依賴幾何論證的基礎上。貝克萊並未否定微積分的正確性。 舉y=x2求導數的例子說明,推導過程確實存在錯誤:前一步假設Δx是不為0的,可以作分母,而後一步又被取為0。那麼到底是不是0呢?牛頓未能自圓其說。
然而,要解決微積分的危機,也就是將其嚴格化,不是一朝一夕的事,又過了150年左右,到19世紀末才完成。包括多位數學家的努力。包括法國的柯西(1789—1857)和德國的魏爾斯特拉斯(1815-1897)。 柯西成功地表達了正確的極限概念,使其成為微分學的堅實基礎。他從數的基礎上(不是從幾何直觀)出發,重新定義了微積分中各種含糊的定義。 柯西定義極限:“如果一個變量的連串值無限地趨向一個固定量,使之最後與後者之差可任意地小,那麼最後這個固定值就被稱為所有其他值的極限。” 那麼任意小是多少?柯西說比你給定的任意數都小。 後來魏爾斯特斯拉認為這個定義不準確和自然,繼續作了修改,提純了極限概念,以ε-δ語言,系統建立了數學分析的嚴謹基礎。。 無窮小不是一個確定的數,也不是零。它是極限為零的變量。研究對象是常量還是變量,是初等數學和高等數學的區別。也是微積分之前和之後數學的區別。微積分的核心概念是導數(微分)瞬時變化率。嚴格定義的無限趨近的極限概念是微積分的精髓。 理髮師悖論—數學第三次危機
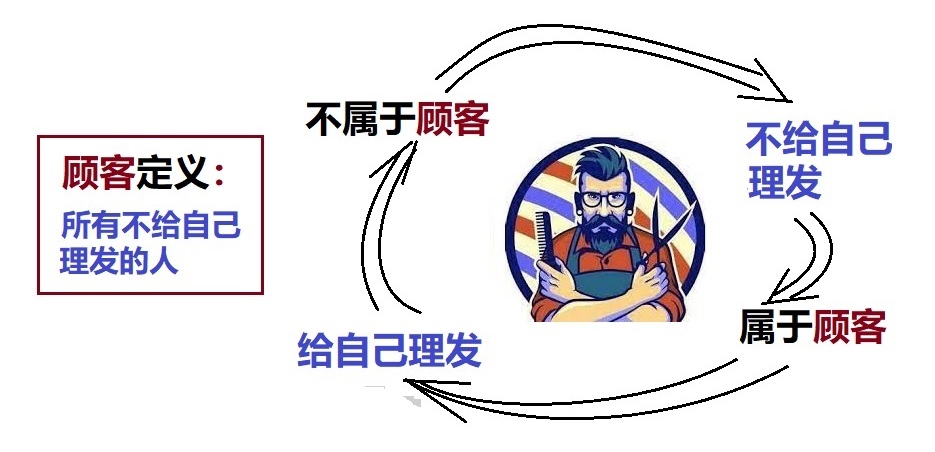
數學上有很多悖論,其實悖論就是矛盾,矛盾產生危機。所以數學的幾次危機也可以用悖論來表述。古希臘時代那次數學危機,起因於希帕索斯發現無理數的“希帕索斯悖論”。第二次無窮小危機則與芝諾悖論及貝克萊質疑牛頓“無窮小量鬼魂”的悖論有關,它的解決為微積分學奠定了堅實的基礎。第三次危機則與有趣的理髮師悖論聯繫在一起。 傳說有一個理髮師,將他的顧客定義為城中所有“不給自己理髮之人”。但某一天,當他想給自已理髮時卻發現他的“顧客”定義是自相矛盾的。因為如果他不給自己理髮,他自己就屬於“顧客”,就應該給自己理髮;但如果他給自己理髮,他自己就不屬於“顧客”了,但他給自己理了發,又是顧客,到底自己算不算顧客?該不該給自己理髮?這邏輯似乎怎麼也理不清楚,由此而構成了“悖論”。 是誰想出這麼一個古怪的燒腦悖論來折騰人?數學發展得好好的,實在像是沒事找事無事生非。的確如此,前兩次數學危機的解決,建立了實數理論和極限理論,最後又因為有了康托的集合論,數學家們興奮激動,認為數學第一次有了“基礎牢靠”的理論。 提出這個悖論的是英國人伯特蘭·羅素。一位出生顯赫的貴族,一個造詣非凡的真正大師。 羅素的家庭了不得,他爺爺曾經出任過英國的兩任首相。羅素自己更了不得,他是著名的歷史學家,哲學家,數學家,各方面多產的大師。他創建分析哲學,提倡自由教育;他的歷史巨著西方哲學史,在哲學界廣為人知;令你沒想到的是,他還獲得了1950年的諾貝爾文學獎。 羅素與羅素悖論(某種意義上等效於理髮師悖論)有關的是一部大塊頭的《數學原理》。洋洋灑灑3 大卷近 2,000 頁,耗費羅素十年功夫折騰得夠嗆才得以完成。羅素認為所有的數學可以約化為邏輯,為此目的作者們使用了極度冗長繁瑣的推理。 比如,花了將近400頁的內容,才得以正確地定義“1”及“1+1”。當年對數學基礎的研究有三大主義。除了羅素信奉的邏輯主義之外,還有德國的希爾伯特為代表的形式主義、 荷蘭數學家布勞威爾為代表的直覺主義。 我們回到理髮師悖論,考慮如何避免理髮師對顧客的定義而產生的邏輯怪圈。如果理髮師修改一下自己的說法:“除了我本人之外,我給所有不給自己理髮的人理髮”,悖論就被避免了。因為理髮師此時定義了一個不包括自己在內的顧客集合,這個集合沒有怪圈!改變定義便能繞過去。對理髮師悖論而言這很容易,對學術上的“集合論”,就不那麼容易了,不過原則差不多。就是在定義集合的時候,要避免“自我”指涉。 還有一個牽涉自我指涉的悖論,叫做“說謊者悖論”,它的典型語言表達為:“我說的話都是假話”。如果你判定這句話是真話,便否定了話中的結論,自相矛盾;如果你判定這句話是假話,那麼引號中的結論又變成了一句真話,仍然產生矛盾。 因此,此類悖論是產生於“集合”的定義牽涉到“自我”指涉,這些悖論解決之後,那麼,如果將自身排除在集合之外,悖論不就解決了嗎?也許問題並非那麼簡單。 幾個悖論都牽涉到“自我”指涉(self-reference)的問題。理髮師不知道該不該給“自己”理髮?說謊者聲稱的是“我”說的話。看起來,將自身包括在“集合”中不是好事,可能會產生出許多意想不到的問題,這些悖論提醒數學家們重新考察集合的定義,康托的集合論對“集合”的定義太原始,以為把任何一堆東西放一起,只要它們具有某種簡單定義的相同性質,就可以數學抽象為“集合”。人們後來將康托的理論稱為“樸素集合論”。為它制定了一些“公理”作為條條框框,從而使得康托的樸素集合論走向了現代的“公理集合論”。 人們認為數學的第三次危機尚未被完全解決,不過屬於邏輯和哲學層面的問題,不太影響數學的發展。 ×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× 本人的科普視頻:YouTube: 天文航天:“談天說地” https://www.youtube.com/playlist?list=PL6YHSDB0mjBLmFkh2_9b9fAlN7C4618gK 趣味數學:數學大觀園 https://www.youtube.com/playlist?list=PL6YHSDB0mjBJifi3hkHL25P3K9T-bmzeA 也發在微信公眾號“天舸”上(微信號:gh_e01fc368fe31):
長按/掃一掃二維碼,敬請關注我的微信公眾號“天舸” ! ×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× |
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2021: | 這裡的華人同胞無偽娘 | |
| 2021: | 多元智能之於赤子之心的內方·外圓 | |
| 2020: | 我們真需要口罩 | |
| 2020: | 在大災難面前有宗教信仰民族和無宗教信 | |
| 2019: | 大家有點緊迫感好不好。時間不等人啊, | |
| 2019: | 漢字密碼:38、碼/碼 | |
| 2018: | 《威福論》,亦叫《腐敗學》。3-24-201 | |
| 2018: | 東窗906:學工程 | |
| 2017: | 胡適對趙元任妻子說:你要寫下去(zt) | |
| 2017: | 再見驢十八:中國之路—從抓革命促生產 | |