| 天蓉:有趣的分形龍(一) |
| 送交者: 天蓉 2011年10月26日16:38:22 於 [教育學術] 發送悄悄話 |
|
把一條細長紙帶對摺,接着把對摺後的紙帶再對摺,又再對摺,重複這樣的對摺幾十次,然後鬆開紙帶,從紙帶側面看過去,我們得到是一條彎彎曲曲的折線。請別小看這個連小孩子都會做的遊戲。從它開始,我們可以探索一連串現代科技中耳熟能詳的名詞:分形、混沌、蝴蝶效應、生命產生、系統科學……
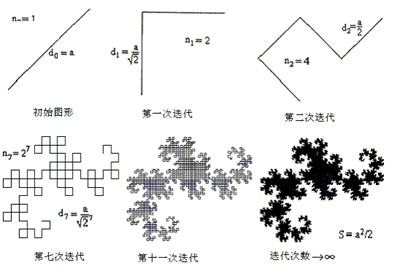
我們把‘紙帶對摺一次’的動作,對應於幾何圖形中的一次‘迭代’,如剛才所描述的循環往復的‘迭代’操作所得到的最終圖形叫做中國龍,或稱分形龍。下圖描述了分形龍曲線的生成過程:
圖一
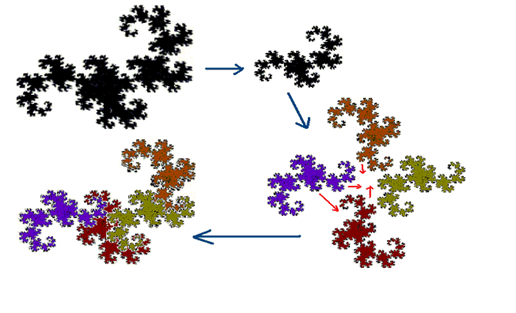
仔細研究上圖中分形龍的產生過程,可觀察到如下三個有趣之處: 1. 簡單的迭代,進行多次之後,產生了越來越複雜的圖形; 2. 越來越複雜的圖形表現出一種‘自相似性’; 3. 迭代次數較少時,曲線看起來是一維折線,此曲線隨着迭代次數的增加而逐漸充滿部分平面。 第一條特點一目了然,無需多言。 第二條的‘自相似性’是什麼意思呢?那是說:一個圖形的自身可以看成是由許多與自己相似的,大小不一的部分組成的。最通俗的‘自相似’例子是中國人喜歡吃的花菜,花菜的每一部分,都可以看成是與整棵花菜結構相似的‘小花菜’。分形龍曲線也具有這種‘自相似性’,從下面的圖中可以看出:分形龍可以看成是由四個更小的但形狀完全一樣的‘小分形龍’組成的。
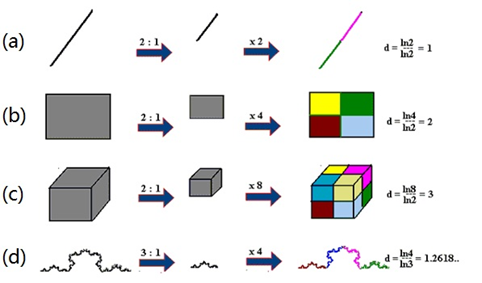
圖二 上述的第三條特點是有關圖形維數的變化:一維的折線隨着迭代次數的增加,逐漸充滿部分平面,看起來變成了二維圖形。 談到幾何圖形的‘維數’,我們不能只憑感覺了,需要更多的數學論證。 分形龍是分形的一個特例,不同的迭代方法,可以形成各種各樣不同的分形,對分形的研究,形成一個新的幾何分支:分形幾何。 其實,在‘分形’這個名字中,就已經包含了‘分數維數’的玄機。眾所周知,經典幾何學中,有1維的線、2維的面、3維的體。三維以內,有現實物理世界的物體對應,容易理解,維數大於三的時候,就需要應用一點想象力了,比如加上了時間的四維空間等。但是不管怎麼樣,經典幾何的‘維數’總是一個整數。而分形幾何中的‘維數’則包含了‘分數維’,這就是‘分形’名稱的來源。如何理解分數維?首先,我們從幾個例子來說明這個分數維的概念。 在經典幾何中,用拓撲的方法來定義”維數” ,也就是說,空間的”維數”等於決定空間中任何一點位置所需要變量的數目:比如,所謂‘三維’,是因為我們需要三個數值來確定一個物體在空間的位置。對於一個二維空間,比如球面,則需要倆個數值來確定一個物體的位置。當汽車行駛在一條高速公路上,它的位置可以用一個數:出口的序號數,來表示。這是一維空間的例子。顯然,按照這種拓撲方法定義的”維數”,只能是整數。 在分形幾何中,我們將拓撲方法定義的‘維數’,擴展成用與自相似性有關的度量方法定義的‘維數’。剛才我們已經介紹了花菜結構和分形龍的‘自相似性’,其實,經典整數維的幾何圖形,諸如一條線段、一個長方形、一個立方體,也具有這種‘自相似性’,比如說,如下圖所示:(a)一條線段是由兩個線段接成的;(b)一個長方形,可以被對稱地剪成四個小長方形,每一個都與原長方形相似;(c)一個立方體,可以被對稱地切成八個小立方體,每一個也與原立方體相似。只不過對經典幾何來說,‘自相似性’顯得太簡單平凡了,沒有什麼特別的新意,我們並不重視它。
圖三 (未完待續)
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2010: | 轉基因衛士們的眼睛是雪亮的 | |
| 2010: | 肖氏手術一例: 現代醫學奇蹟 | |
| 2009: | 駁斥5味西岸的:海龜骨感說,健談民族 | |
| 2009: | 有理性的信仰:信仰和理性 | |
| 2008: | 華人在美國政治地位低下的2大根本原因 | |
| 2008: | 無為而治是當今世界的管理主導 | |
| 2007: | 多數中國大學學報是學術垃圾生產地 | |
| 2007: | 中國研究生很少有一流成果的可能原因 | |
| 2006: | 說說中醫藥的中國標準 | |
| 2006: | 聞方舟子好太極之隨感 | |