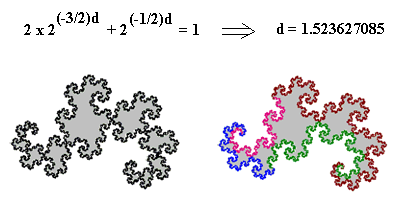| 天蓉:有趣的分形龍(二) |
| 送交者: 天蓉 2011年10月27日13:21:59 於 [教育學術] 發送悄悄話 |
|
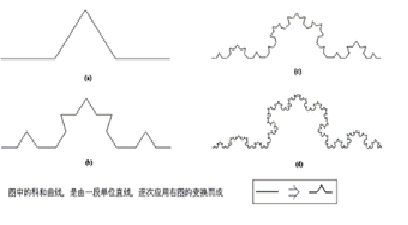
不過現在,我們可以利用這種‘自相似性’,重新定義幾何圖形的‘維數’。 仍然利用上面的圖,用自相似性來定義的‘維數’可以如此簡單而直觀地理解:首先將圖形按照(N: 1)的比例縮小,然後,如果原來的圖形 可以由(M)個縮小之後的圖形拼成的話,這個圖形的‘維數’d,就等於 ln(M)/ln(N)。不難看出,將上述方法用來分析直線、平面、空間,分別得到d = 1、2、3(上圖中的a、b、c)。 上圖中的(d),是一種很簡單的分形,叫做科和曲線,也是一種自相似圖形,它的迭代生成過程如下圖所示。
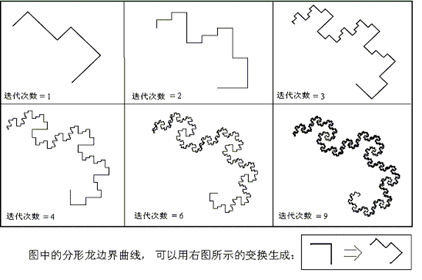
圖四 可以用同樣的方法分析如圖(d)及上圖所示的科和曲線:首先,將科和曲線的尺寸縮小至三分之一;然後,用四個這樣的‘小科和曲線’,便能構成與原來一模一樣的科和曲線。因此,我們得到科和曲線的維數d = ln(4)/ln(3) = 1.2618..。這就說明了,科和曲線的維數不是一個整數,而是一個小數,或分數。 下面,我們再回頭研究分形龍的維數(圖二)。將圖中的分形龍曲線,尺寸縮小為原來的一半之後,得到右上圖的小分形龍曲線。然後,將四個小分形龍曲線,分別旋轉方向,成為如右下圖的位置。最後,再按照右下圖中箭頭所指的方向,移動四個小分形龍曲線,便拼成了左下圖的、與原來曲線一樣的分形龍曲線。因此,如此可以證明,分形龍曲線的維數為2,因為(d = ln(4)/ln(2) = 2)。 有趣的是,分形龍圖形的邊界也是一個可以用迭代法產生的分形: 圖五 由圖六可知,整個分形龍曲線的邊界是由四段相似的圖形組成的。這種分形的維數估算方法比較複雜一些,它的“分形維數“(d)可以通過解如下方程求得:
通過分形龍,我們認識了分形,理解了分數維。分形幾何是理解混沌概念及非線性動力學的基礎,在現代科學技術中,有着廣泛的應用。
下面的連接可以讓你親身體會分形龍圖形的趣味和美妙: http://www.tianfangyetan.net/cd/java/fractals.html
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2010: | 若論造假肖傳國確實不如方舟子,有意賣 | |
| 2010: | 中國人的英語水平越來越高了。廣州亞運 | |
| 2009: | 美國學術圈也不乾淨 | |
| 2009: | 別太拿塗博士的死說事--也為浙大說幾句 | |
| 2008: | 估計,清華這次要出醜 | |
| 2008: | 憑什麼要永遠看王元用數學知識買的那隻 | |
| 2007: | aa88:“楊振寧談嫦娥奔月”讀後感 | |
| 2007: | 朋竹:我在中科院的經歷 | |
| 2006: | 一個南開大學生對十大名校的評價 | |
| 2006: | 科研上【effects】and 【dosage】的關 | |