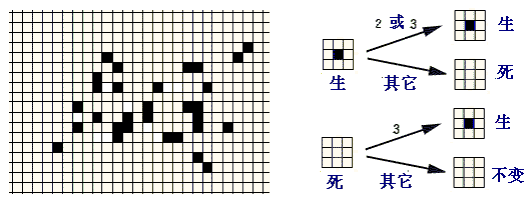
一九七零年十月, 美國趣味數學大師馬丁·加德納通過”科學美國人”雜誌的”數學遊戲”專欄, 介紹給讀者一個有趣的數學遊戲 - 康維的“生命”遊戲。一時吸引了一大批人的興趣。

生命遊戲事實上並不是通常意義上的”遊戲”, 它沒有遊戲玩家各方之間的競爭, 也談不上輸贏，可以把它歸類為“仿真遊戲”。事實上，也是因為它模擬和顯示的圖象，看起來頗似生命的出生和繁衍過程而得名為“生命”。遊戲在一個類似於圍棋棋盤一樣的，可以無限延伸的二維方格網中進行。例如，設想每個方格中都可放置一個生命細胞，生命細胞只有兩種狀態：“生”或“死”。如下圖4-1中，用黑色的方格表示該細胞為“生”, 空格表示該細胞為“死” 。遊戲開始時, 每個細胞可以隨機地（或給定地）被設定為“生”或“死”之一的某個狀態, 然後，再根據某種規則（生存定律）計算下一代每個細胞的狀態：

例如，我們可以規定如下的‘生存定律’：

1．   每個細胞的狀態由該細胞及周圍八個細胞上一次的狀態所決定；

2.       如果一個細胞周圍有3個細胞為生，則該細胞為生，即該細胞若原先為死，則轉為生，若原先為生，則保持不變；

3.      如果一個細胞周圍有2個細胞為生，則該細胞的生死狀態保持不變；

4.      在其它情況下，該細胞為死，即該細胞若原先為生，則轉為死，若原先為死，則保持不變。

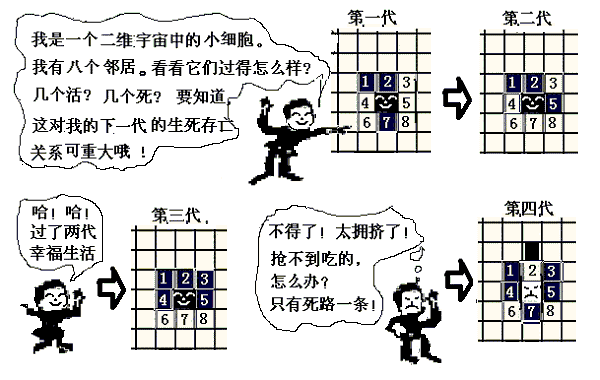
然後，同時更新所有的狀態，得到第二代的分布圖。這樣一代一代地作下去，以至無窮。比如說，在下面的圖4-2中，從第一代開始，畫出了四代細胞分布的變化情況。第一代時，在中心處有四個活細胞，然後，讀者可以根據以上所述的四條生存定律，得到第二、三、四代的情況，觀察並驗證下圖的結論。

  四代二維生命細胞的演化過程

你可能會說，這樣的遊戲玩起來太不方便了！一格一格地算半天才走一步，也看不出趣味在何處。不過，相信你不會忘記，我們有一個最好的幫手：計算機。我們可以根據四條生存定律編好程序，輸入初始狀態圖，用計算機來進行運算和顯示。有了計算機的幫助，就不難發現生命遊戲的趣味所在了。例如，如果你選擇“隨機設置”初始狀態，你會看到，遊戲開始運行後，迭代過程中細胞生生死死，增增減減，變幻無窮。也許，屏幕上“生命細胞”的圖案運動變化的情況，會使你聯想到自然界中某種生態系統的變化規律：如果一個生命，其周圍的同類過於稀疏，生命太少的話，會由於相互隔絕，失去支持，得不到幫助而死亡；如果其周圍的同類太多而過於擁擠時，則也會因為缺少生存空間，且得不到足夠的資源而死亡。只有處於合適環境的細胞才會非常活躍，能夠自我複製，並進行傳播。

我們又一次地悟出這個道理：“複雜的事物（即使生命！），原來也可以來自於幾條簡單的規律！”。生命遊戲繼分形和混沌之後，又為我們提供了一個觀察從簡單到複雜的好方式。

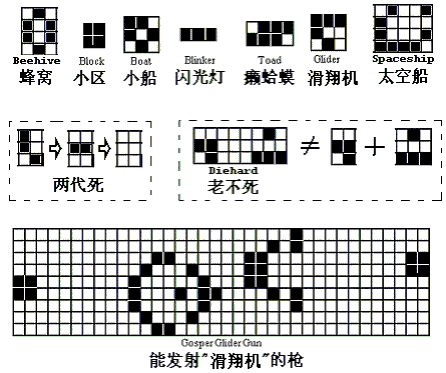
“生命是如何產生出來的？”，這是一直困惑着我們的大問題。如今這個所謂的“生命遊戲”，是否能為解決此問題提供一些有用的線索呢？讓我們首先從下面圖中所示的，生命遊戲中幾種特別類型的分布圖案說起。

生命遊戲中幾種特別類型的分布圖案

 儘管生命遊戲中每一個小細胞所遵循的生存規律都是一樣的，但由它們所構成的不同形狀的圖案的演化行為卻各不相同。這個現象可以用古希臘哲學家亞里士多德的古老命題“整體大於它的各部分之和” 來表達。不同演化行為的圖案大致有如下幾種類型：靜止型、振動型、運動型、死亡型、不定型。

 圖4-3中的“蜂窩”，“小區” 和“小船”，都屬於靜止型的圖案，如果沒有外界的干擾的話，此類圖案一旦出現後，便固定不再變化；而“閃光燈”，“癩蛤蟆”等，是由幾種圖形在原地反覆循環地出現而形成的振動型；圖中右上角的“滑翔機”和“太空船”，則可歸於運動類，它們會一邊變換圖形，一邊又移動向前。如果你自己用生命遊戲的程序隨意地試驗其它一些簡單圖案的話，你就會發現：某些圖案經過若干代的演化之後，會成為靜止、振動、運動中的一種，或者是它們的混合物。

此外，也還有可能得到我們尚未提及的另外兩種結果：一類是最終會走向死亡，完全消失的圖案；另一類是永遠不定變化的情形。就拿“最終死亡”的情況來說吧，“死”的速度可是有快有慢，有的曇花一現，不過幾代就斷子絕孫了（圖中的兩代死）；有的倒能繁榮昌盛幾百上千代：如上圖中間的第二個例子就能堅持130代。有趣的是，上例中“老不死”是由兩個分圖案構成的，這兩個分圖案如果單獨存在，都會長生不死，糾集在一塊兒後，儘管也延續了130代，結果卻不一樣，這又是一個“整體不等於部分之和”的實例。從變幻莫測的生命遊戲中，還有許許多多諸如此類的趣事，就無法一一列舉了。

敘述至此，應該插入一段歷史了。剛才所說的遊戲，被稱為“康維的生命遊戲”，康維，何許人也？為何憑空想出了這生命遊戲？

現為美國普林斯頓大學數學教授的約翰·康維，除了致力於群論、數論、紐結理論及編碼理論這些多方純數學領域之外，也是遊戲的熱心研究者和發明者。在眾多貢獻之中，他的兩個最重要的成果都與遊戲有關：一是他在分析研究圍棋棋譜時發現了超實數（Surreal Number）；其二便是他在英國劍橋大學時發明的生命遊戲使他名聲大振，特別是經由《科學美國人》連續兩期的介紹推廣後，康維的名字在７０年代的知識界幾乎家喻戶曉。上世紀的７０年代初，使用計算機還只是少數科研人員的專利，對生命遊戲中圖案演化行為的研究，有些熱心者甚至業餘時在紙上進行！鋸馬丁·加德納後來回憶所述，當時整個國家科研基金的用途中，可能有價值上百萬美元的計算機時間，花費於並不十分合法的對“生命”遊戲的探索。業餘愛好者瘋魔於此遊戲的規則簡單卻變化無窮; 生物學家從中看到了”生態平衡”的仿真過程; 物理學家聯想到某種似曾相識的統計模型;而計算機科學家們則競相研究“生命遊戲”程序的特點, 最後，終於證明了此遊戲與圖靈機等價的結論（關於圖靈機，後面將有所介紹）。對生命遊戲過分的熱心和瘋狂，大大超出了《科學美國人》的“數學遊戲”專欄的負荷能力，以至於當時還專門為此推出了一個名為《生命線》的通訊刊物。

另一件值得一提的趣事是：康維設置了一個五十美元的小獎金，給第一個能證明生命遊戲中圖形能（或不能）無限制增長的人。這個問題很快就被麻省理工學院的計算機迷Bill Gosper解決了，這就是我們上面的圖4-3中最下面一個圖案“滑翔機槍”的來源。下面的圖4-4所示的是滑翔機槍在計算機上運行的圖形：一個一個的“滑翔機”永不停止地、綿綿不斷地被“槍”發射出來。

  生命遊戲中的滑翔機槍

這個實例證明了生命遊戲中存在無限增長的情形，看起來的確令人鼓舞：由幾條簡單的“生存定律”構成的“宇宙”中的“槍”，能不斷地產生出某種東西，就象機器製造出產品一樣。這樣一來，是否再進一步，就有可能找到某種圖案在演化過程中能自我複製，象生命形成的過程一樣呢？如果那樣的話，在計算機上模擬生命的複製、進化、突變等現象，似乎已經曙光初現；掌握製造生命的機制，是否也為時不遠了呢？

生命遊戲程序的連接：

http://www.tianfangyetan.net/cd/java/Life.html