| 天蓉:走近量子(13)從糾纏態到qubit |
| 送交者: 天蓉 2012年03月04日15:59:14 於 [教育學術] 發送悄悄話 |
|
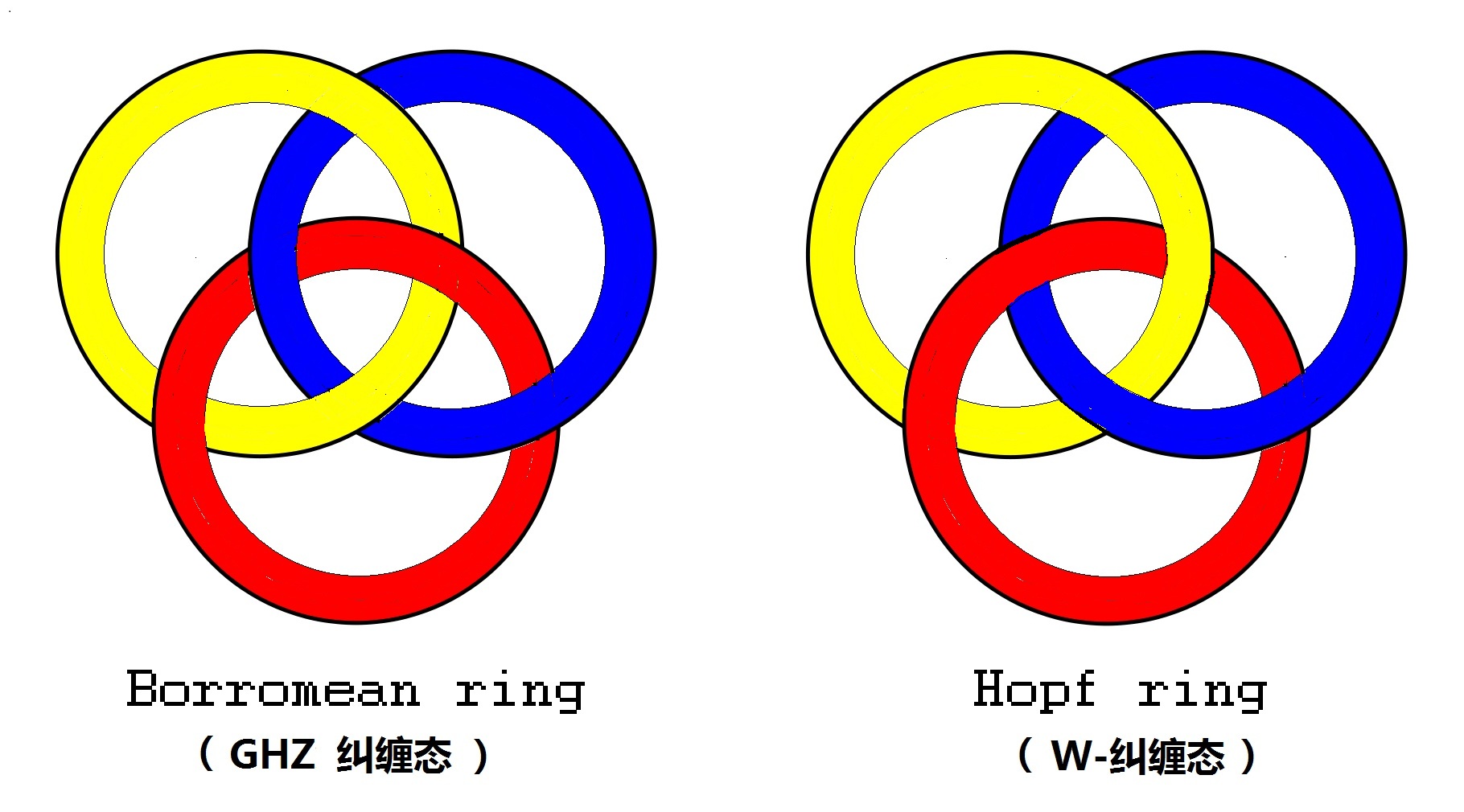
使用我們在第8節中表述糾纏態時所用的簡單數學,描述一下三粒子糾纏時的狀態。 現在,我們有三個粒子A、B和C,它們分別都有兩種定態0、1(A1 、A0 、B1 、B0和C1 C0)。因此,它們的單粒子定態可以組成8種三粒子定態∶ |111>、|110>、|101>、|100>、|011>、|010>、|001>、|000>。 (12.1) 這兒使用了狄拉克符號來表示三粒子的狀態。狄拉克符號其實很簡單,只不過是給原來代表狀態的字母或數字兩邊,加上了一件由左右兩個符號∶|>,製成的外套而已。套上了這件外套,所表示的狀態看起來,要比接連寫一串數字或字母,意義清楚明了多了,並且還多了一層‘量子’的意思。比如說,我們用|111>來表示三個粒子A、B和C都是1的那種量子狀態。這兒的0和1,對電子來說,對應於不同的自旋;對光子來說,則對應於不同的偏振方向。其實,狄拉克創造的外套符號有兩種。除了我們在(12.1)中用過的右矢|>(英文名ket)之外,還有一個左矢<|(英文名bra),我們以後也將會碰到。 讀者可能還會發現,(12.1)中所列出的8種狀態,與計算機數學中使用的二進制中,3個比特所能表達的所有2進制數值非常相像。不錯,這正是我們本節的後半部分要介紹的qubit。在這兒,狄拉克ket外套|>起到了作用,使它們看起來才有別於經典計算機科學中所說的bit! 和以前介紹過的雙粒子糾纏態類似,從(12.1)中列出的的8種三粒子定態,我們可以組成無數多種糾纏態。其中格林伯格等人感興趣的,是後來被人們稱作GHZ態的那一種量子態。GHZ態可以寫成如下表達式∶ |GHZ> = |111> + |000> (12.2) 按照前面幾節的慣例,我們在公式(12.2)中,略去了歸一化係數(sqrt(2))-1。以後也都照此辦理。 這個GHZ糾纏態是什厶意思呢?類似於對雙粒子糾纏態的解釋,我們可以這樣說∶這個態是兩個三粒子本徵量子定態|111>和|000>的疊加態。再來複習複習前面幾節中介紹過的所謂‘疊加’的意思∶當我們描述電子干涉雙縫實驗時,‘疊加’意味着電子同時通過兩條縫,既穿過縫1,又穿過縫2。所以,這兒|111>和|000>的‘疊加’ 就應該意味着,這個三粒子體系既是|111>,又是|000>,或言之∶同時是定態|111>和定態|000>。如果使用哥本哈根派波函數塌縮的詮釋說法∶在測量之前,三個粒子是什厶狀態我們完全不能準確地說清楚。但是,只要我們一旦測量其中一個粒子,比如說,我們如果在z方向測量粒子A的自旋,其結果是|1>,那厶,另外兩個粒子z方向的自旋狀態也立即分別塌縮為|1>;如果我們測量其中一個粒子(A)在z方向的自旋,結果是|0>,那厶,另外兩個粒子z方向的自旋狀態也立即塌縮為|0>。在上述說法中,如果被測量的不是粒子A,而是B或C,另外兩個粒子也將遵循類似的塌縮過程。 使用更嚴格的數學,可以證明∶GHZ糾纏態是三粒子量子態中糾纏度最大的態。我們在這兒談到了糾纏度的大小,卻尚未對糾纏度下定義。說實話,對糾纏度至今還沒有一個公認的明確定義。一般可以用量子統計中使用的馮·諾伊曼‘熵’來定義糾纏度,但這就越扯越遠,越扯越專業化了,就此打住。 除了GHZ糾纏態之外,在量子信息中又有人研究一種三粒子糾纏態中的W-態∶ |W> = |100> + |010> + |001> (12.3) 下圖用一個很直觀的圖像描述,來表示GHZ糾纏態和W-糾纏態的區別∶
三粒子糾纏態和Knot理論
GHZ態和W-態分別對應於knot theory中的Borromean ring和Hopf ring。從上圖中很容易看出兩種結腹的區別。如果我們斷開圖中左邊Borromean ring三個圓環中的任何一個,其餘兩個圓環也立即分開了,這點性質可以對應於剛才我們所描述的GHZ態的量子力學特徵∶如果一旦測量三粒子系統中的任何一個粒子,其餘兩個粒子也立即分別塌縮為它們各自的單粒子定態。但是,如果我們考察圖中右邊的Hopf ring就會發現,當剪開三個圓環中的任何一個時,另外兩個圓環並未被分開,仍然糾纏在一起。這種knot的性質也有它的量子力學對應∶從W-態的表達式(12.2)中看出。當測量其中一個粒子而結果為|0>的時候,另外兩個粒子塌縮到不能分 的雙粒子糾纏態∶|10> + |01>。
GHZ態和W-態是兩類完全不同的糾纏態,不能互相轉換。對三粒子系統的GHZ態和W-態可以很容易地推廣到n粒子系統。用量子計算的語言來說,表達式(12.2)和(12.3)可以很容易地從3-qubit(3位量子元)系統,推廣到n-qubit(n位量子元)系統。
現在,我們解釋一下,什厶叫qubit(或稱q-比特)?類似於比特,它所表示的是量子計算機技術中的一個存儲單位。隨着計算機和網絡走進社會,走進人們的日常生活,有關‘比特’,‘二進制’等概念幾乎已經家喻戶曉。而現在在本文中,我們在‘比特’這個詞前面,加上了一個q,本文討論的又是量子(quantum)問題,qubit的意義便顯而易見了,那不就是一個‘量子比特’嗎?
然而,重要的是,一個‘量子比特’和一個‘比特’,本質上有些什厶相同及不同之處呢?很幸運,我們在前面表示三粒子糾纏時,用的是0和1,這和計算機中表示‘比特’和‘二進制’的符號是完全一致的,這是量子比特和比特的共同點,至於它們的不同之處,可以從物理和算法兩種角度來理解。
我們首先從物理的角度來看‘比特’∶在經典計算機的電子線路中,一般是經由介質中某點電壓的‘高’和‘低’兩種不同的物理狀態來表示數學中的‘0’和‘1’。比如說,我們可以將大於0.5伏特的電壓狀態,規定為‘1’,小於0.5伏特的電壓狀態,規定為‘0’。這樣,在一個確定的時刻,某點的電壓或者是‘高’,或者是‘低’,也就是說,一個寄存器的輸出,要厶是‘1’,要厶是‘0’,兩種狀態中只能取其中之一。這是由經典物理的決定性所決定的。這個或0或1的電壓輸出,就可以用來表示一個‘比特‘。
看到這兒,讀者們已經預料到了,既然用經典的電壓高低狀態來表示比特,那厶,本文中討論了半天的量子態,就可以用來在物理上實現一個‘量子比特’。比如說,電子的自旋有‘上’‘下’之分,光子的園偏振方向有‘左’‘右’之別,這些量子力學中的物理量都可以用來對應於1和0兩個數字,腹成‘量子比特’。
談到量子比特的特別之處,又回到了我們貫穿此文的,嘮嘮叨叨不斷說到的一個量子現象的基本特點∶那種“既是此,又是彼”的疊加態。也就是說,量子力學中的物理量都是分立的、不連續的、幾率的。不存在那種類似經典力學中的‘在確定的時刻,確定的輸出電壓’的概念。所以,一個‘量子比特’在一個確定時刻的數值,是非決定性的。既是‘上’,又是‘下’,同時是‘0’又是‘1’。
‘量子比特’和‘比特’在算法意義上的不同,也是基於用以表達它們的物理狀態的不同。我們知道,一個經典的比特有0和1兩種狀態,可以用它來表示0,或者表示1,但只是表示0、1中的其中一個。而一個量子比特同時有0和1兩種狀態,因此,就可以用它來表示0,也表示1,同時代表兩個數。‘一個數’和‘兩個數’,差別不大,但如果是3個比特(或3個量子比特)放在一起,就有些差別了。三個經典比特有了8個不同的狀態,但仍然只能表示0-7之間的一個數。如果是三個量子比特組成的系統,就不一樣了。那種情形下,可以同時存在8種不同的狀態,因此,它可以用來同時代表0-7這8個數。
現在,假設我們有了一個3-qubit系統腹成的計算器,我們可以進行計算了。比如說,將它乘以5。當我們輸入5,並發出運算指令後,這個3-qubit系統中0-7的所有8個數都開始進行運算,並同時得出8個結果來!令人吃 吧,這比較起一個經典的3-bit系統只能得到一個結果來說,運算速度不是快了8倍嗎?因為它相當於8個經典計算器同時進行平行運算。可不要小看這個8倍,如果把它看成是2**3的指數形式,意義就大了。假設我們的量子計算機有100qubit,或者更多的話,你不妨計算一下,計算速度將增快多少?
用一個通俗的比喻,也就是說,經典的原則是∶‘魚’和‘熊掌’,不能兼得;而在量子世界中,‘魚’和‘熊掌’竟然可以兼得!這樣,一台量子計算機就可以相當於有多台,並且是指數倍增長的多台經典計算機,在同時進行平行運算。可想而知,那速度當然快囉!
上一篇∶GHZ登場 下一篇∶更多qubit
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | 全美亞裔年度傑出工程師頒獎 華裔囊括 | |
| 2011: | 地上的人類,百分之九十九點九九都是這 | |
| 2010: | 科普是這樣被來玩的嗎? | |
| 2010: | 鄭重聲明: | |
| 2009: | 空軍大院:中國人中為什麼沒有“世界級 | |
| 2009: | 中國教育的罪狀 | |
| 2008: | 鬧了半天美國教授的工資沒警察高? | |
| 2008: | 北大才女: 我從來就不追星。我跟湯姆克 | |
| 2007: | 赴美讀博,你動心了嗎 | |
| 2007: | 在美國生活,太多的困惑源於自己 | |