| 天蓉:走近量子(17)量子計算機 |
| 送交者: 天蓉 2012年03月18日17:07:28 於 [教育學術] 發送悄悄話 |
|
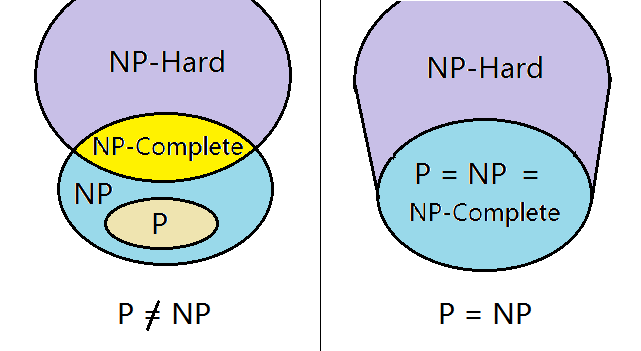
波士頓哈佛大學附近的CLAY數學研究所,千禧年時曾經發佈一則消息:將提供百萬美元的獎金為七個當時未解決的數學問題徵求答案。目前為止,12年過去了,只有其中一個“龐加萊猜想”的問題被俄國數學家佩雷爾曼Grigori Perelman於2006年解決。但佩雷爾曼天生淡泊名利,拒絕領獎,也拒絕了同年頒發給他的數學界的諾貝爾獎“菲爾茲”獎,據說此事還在數學界與某數學家演繹出一段幕後故事,不過這是題外話,在此不表。 這七大千禧獎中有一個,是在計算機算法領域頗為著名的 P / NP 問題。 眾所周知,計算機的發明為許多必須進行大量數字計算的問題提供了一條捷徑。計算機的計算能力是一般的人工計算無法比擬的。一個超級計算機可以以每秒鐘進行億萬次運算的速度連續不停地進行運算。一般來說,需要進行數字計算的問題的運算量的大小與表徵這個問題大小的變量數目N有關。變量數N越大,解決問題所需的計算時間T也越長。當然,計算時間T也取決於所使用的計算方法。計算機算法就是研究各種計算方法的學問。 所需計算量T與變量數N之間的函數關係因為問題的不同而不同。在有些問題中,T與N成線性關係;而在另一些問題中,則成平方關係;也有可能是隨着N的增加而指數增長。 研究算法的科學家們,將需要進行大量計算的問題,按照T隨N而增大的函數形式,分為幾種不同的類型。第一種叫P型,或稱多項式型。計算P型問題所需的時間T與N成多項式級數關係。多項式型問題是計算機可以解決的問題。只要計算機的速度足夠快,內存足夠大,使用了正確的算法,答案總會即日可待。而另一種NP型的問題,還沒有找到任何成功的算法,使得問題的答案能在與N成多項式級數關係增長的時間內解出。但這並不能說明這種算法不存在。所以,這是屬於不能確定T與N是否是多項式級數關係的一類問題。此外,還有一類最困難的問題,屬於NP-Hard。 在NP型中,有一個數學家們最感興趣的子集,叫做NP完整型。這個子集中的任何兩個問題互相轉換所需的時間與N成多項式級數關係。因此,如果找到了一種多項式的算法,解決某個NP完整問題,也就有了多項式的算法,解決所有的NP完整問題,這也就是叫做證明了“NP=P”。反之,如果你能夠證明,這種對NP完整型的多項式算法並不存在的話,你就證明了“NP!=P”。CLAY數學研究所的百萬大獎,就將頒發給證明了“NP=P”,或者“NP!=P”的人。 看看下面的圖,可能更容易理解P / NP 問題:
大多數的數學家們都相信,結論應該是P!=NP,但是要想真正嚴格地證明這個結論卻非常困難,否則怎麼會有百萬美金的大獎來徵求答案呢?不過,2010年8月,曾經有一個惠普實驗室的研究員,聲稱證明了P不等於NP。但他當時只在自己的網站上宣稱此事,後來似乎便沒有了下文。所以,這應該仍然是一個未解決的問題。 算法問題的實質是計算速度的問題。從理論上來說,現在的這種經典類型的計算機永遠處理不了那些計算量按指數增長的問題。這些題目包括著名的“旅行推銷員問題”、用於保密通訊的大數的質數分解問題等,還有據說是屬於最難的NP-Hard類的圍棋必勝問題。不敢說量子計算機都能解決這些困難,但總是提供了一種完全不同於經典圖靈機,而是按照量子規律來運行的另一類選擇性吧。 遺憾的是,量子理論誕生已有一百年左右的歷史,經典計算機使用的芯片製造技術也早已涉及到量子理論,但工作在數億個經典比特基礎上的計算機科學家們,竟晚了大半個世紀,才認識了量子計算。如果早些進行這方面的研究的話,計算機科學也許受益匪淺。回顧計算機發展的歷史,從第一台經典計算機問世以來,它在‘尺寸大小’的領域經過了天翻地覆的變化,從一個占據幾棟樓房的龐然大物縮小到了人們的手掌上、口袋裡。近二十年,計算機技術更是經歷了巨大的革命的飛躍,單個芯片上三極管的數目及運算的速度都是以指數形勢逐年上升。正是這種高速發展,使經典計算機將很快達到它的極限。那時的三極管的大小將達到原子的尺度。經典計算機,無論是40多年前的充滿整棟屋的龐然大物,還是現在的手機型電腦,基本原理卻是萬變不離其宗,基本構造單元都是比特(bit),不論是用燈泡大小的電子管來實現的一個比特,還是用芯片上的三極管(微米級大小)來表示的比特,都是同樣遵循牛頓力學定律。直到費曼觀察到用經典計算機模擬量子系統時的 “指數減慢”問題,才促使計算機科學家和物理學家牽手合作,正式啟動了研究“量子計算機”的物理實現及算法問題。 也有人將研究“可逆計算” 的IBM科學家R. Landauer譽為量子計算之父。認為他在1961年“可逆計算”領域的發現而導致了量子計算機研究。但實際上,可逆計算的研究只是與量子計算機有關係,並未直接導致量子計算的發展,並且,R. Landauer本人生前(直到1999年去世)都一直不遺餘力地批評量子計算機研究。他認為量子計算機“沒有考慮各種可能的噪音源,沒有考慮實際生產的誤差和缺陷,基本沒戲。” 當然,雖然費曼早在1982年就預見到量子元件的超強計算功能,但直到1996年,貝爾實驗室的W.Shor發展出一種算法之後,有關量子計算機的研究才逐漸成為學術界及一些大型工業研究部門的矚目課題。計算機學者開始使用和了解奇妙的量子力學規律,物理學家們也將眼光投向計算機科學,關心和探討適合量子元件運算規律的算法。如果將W.Shor的算法,用在量子計算機上的話,可以在多項式的時間內,將一個大的整數分解為若干質數之乘積。也就是說,如果未來造出了真正實用的量子計算機,在它上面使用W.Shor算法及其它量子算法,前面所說的NP問題,便有可能轉換成P型問題。 2001年初,IBM研究中心的科學家們研製出了只有五個比特的量子計算機,並成功地用它進行order finding的計算,為實現W.Shor的算法邁出了第一步。 一個經典計算機的儲存量可以用比特的多少來衡量。它運算的快慢可以由每秒鐘能進行的比特的轉換數目來決定。量子計算機也是如此,只是構成它的最小信息單元不同於經典的比特,而是前面介紹過的量子比特。 儘管量子計算機的潛力看來似乎很大,實現起來卻困難重重。量子比特數目的增加談何容易!我們現在所使用的手提電腦,硬盤儲存量少說也有幾十億個比特,可是,如前面所說,IBM研究中心當時研製出了只有五個比特的量子計算器件,就已引起轟動。 如上幾節所述,量子計算器件的潛力的來源是在於量子系統在不與環境互相作用時的不確定性。一旦與環境相互作用,量子器件就會崩塌到一個確定的狀態,計算便無法進行下去。困難在於:如何才能將量子計算系統與其環境分開來,使其既能維持它的獨立運算能力,而又需要可接近,使人得以控制計算過程,並得到輸出結果呢? 要作到以上所述的環境是非常困難的。這也就是為什麼,直到近十年來,才有幾個實驗室,只實現了少數十來個量子比特的計算器件。這些器件有的是基於核磁共振NMR(類似於成象所用的MRI)的實驗。實驗時,在NMR的機器核心上,撒上一些fluerinated有機液體,然後,通以RF脈衝來激勵液體,使其轉化成高速處理器,而解決問題的算法便被編碼到RF脈衝里。有的是基於3維超導量子比特的計算器件, 下圖是IBM的3量子比特的硅片。
(scale: 8mm x 4mm) 照片來自網絡,參考IBM的最新報道: http://www-03.ibm.com/press/us/en/pressrelease/36901.wss 2011年5月,量子計算機領域飛奔出了一匹黑馬。加拿大D-Wave公司公布他們造出了第一台128量子比特的“商用量子計算機”- D-Wave-One,還據說賣出了一個單價1000萬美金的天價,買主是美國的洛克希勒馬丁公司。這個消息一經發布,在業內引起一陣軒然大波。不少量子計算機方面的專家質疑D-Wave-One能否稱得上是一台真正意義上的“量子計算機”? D-Wave聲稱他們的這個超導絕熱的量子計算機,使用了所謂“量子退火算法”,可以比經典算法效率更高地解決離散最優化問題。不過,也只能解決這一種特殊用途的問題。因此,當然不是一台通用意義下的量子計算機。有人認為,頂多是一個費曼所提到過的只能解決某一類問題的仿真機器,至於這個仿真過程有多少量子的成分,人們也不清楚。在他們的博客網頁上,對“離散最優化問題”等有一些普及性的描述,有興趣的讀者可去一閱: http://dwave.wordpress.com/2011/05/11/learning-to-program-the-d-wave-one/ 要實現通用的量子計算,滿足不同的計算要求,運行各種量子算法,實現輸入、輸出、和保持量子相干態和糾纏態來進行可靠的運算,是極端困難的。此外,量子計算糾錯的問題很難解決。專家們認為,製造出通用、可靠的量子計算機,還有很長的路要走。 即使是進行實驗的專家們自己,也很難從他們現在進行的實驗,來描述和想象將來量子計算機的形態。因此,科學家們不斷把眼光投向新的物理領域,提出種種設想:能否不使用超導?也許用固態NMR?也許用被激光俘獲後的冷卻離子?也許,量子計算機根本不應該象經典計算機似的用製造芯片的人工技術製造出來,而應該與生物工程、基因研究等結合起來?的確,生物體的生長過程,證明了大自然本身已經完成了人類想人工達到的目的的最困難部分。在生物體內,普通分子便已經會按照量子規律做最複雜的計算,量子計算機已經存在於自然之中,人類又何必多此一舉呢。當然,科學家和工程師們總是在不停止地探索物質的奧秘,發展更先進的技術,製造出更新的東西,他們是永遠不會放棄的。
下一篇:量子隱形傳輸 |
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | 日本為什麼在核電廠儲存了6735根核 | |
| 2011: | 肖傳國刑滿釋放後會幹啥 / 作者:Cheng | |
| 2010: | “行百里者半九十”新譯 | |
| 2010: | 行百者半九十,又一個譯法。 | |
| 2009: | 我再申明幾點 | |
| 2009: | 回復恩典 | |
| 2008: | 孔子是創新型聖人 | |
| 2008: | 誰來養活美國:美國人如何退休? | |