这个西洋人通过观察和计算发现了兔子繁殖的规律，那便是假设兔子不死，那么从第三个月开始每一个月兔子的总数都会是前两个月数目之和，于是他得出了这样一个数列： 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368。写成公式便是 F（n）=F(n-1)+F(n-2)（n≥2，n∈N*；F(1) = 1 ）。这个以递归方式定义的公式便以这位西洋人的名字作为公式名，叫做“斐波那契数列”（Fibonacci Sequence), 又因之从兔子繁殖规律而来，也叫做“兔子数列”。再后来有个叫Robert Simson的苏格兰人证明了当项数趋于无穷时，斐波那契数列的后项与前项之比趋近黄金分割，也就是1.61803398875…，说明了斐波那契数列与黄金分割有天然的联系，所以又叫“黄金分割数列“）。

    他的全名叫里昂纳多.斐波那契（Leonardoda Fibonacc), 意大利比萨人，人称”比萨的里昂纳多”，生于公元1170（一说1175）卒于1245年（一说1250）。因为父亲出任比萨商团外交使节的缘故，他曾跟随他的父亲在北非生活，从而接触了印度和阿拉伯的数学。公元1202年27岁那年，斐波那契撰写了著名的《算盘全书》（Liber Abacci--Book of Calculation）一书，成为第一个研究了印度和阿拉伯数学理论的欧洲人。他写作这本书的主要目的是鼓励欧洲人使用印度0到9的数字系统（०, १, २, ३, ४, ५, ६, ७, ८, ९ ) 而抛弃罗马的( I,II,III, IV...)，因为他发现相比于罗马数字系统，印度-阿拉伯数字系统应用于商业和金融上具有相当强的优越性。德国人文主义作家格雷戈尔·赖施（Gregor Reisch）在他1503年出版的《哲学的珍宝》（Margarita Philosophica）一书中有一幅插图，说明了那个时代的欧洲人对印度-阿拉伯数字的推崇：

图中右边的是古希腊数学家毕达哥拉斯正在用一块计数板在计算，神情无奈，而左边的人用印度数字计算则兴高采烈，中间代表算术的女人裙子上写满了醒目的阿拉伯数字。

    当然他最著名的贡献还是发现了“斐波那契数列”。这个数列描述了很多自然现象和规律，特别在植物学领域。很多的植物的花瓣比如百合花，三角梅，玫瑰，菊花等都以某个斐波那契数组成。

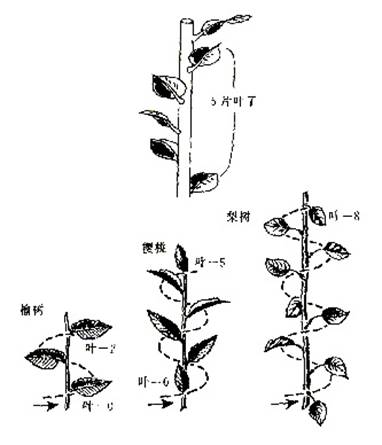
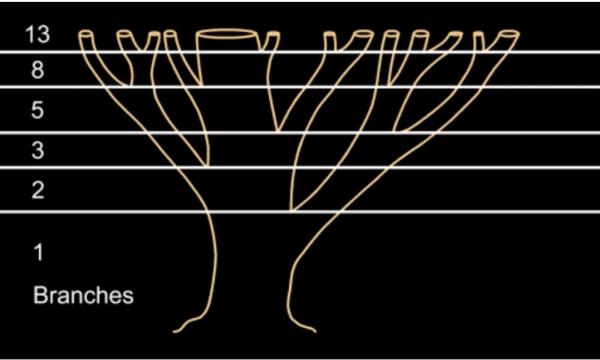
树叶排列树干的生长也符合斐波那契数列的规律：

•    比如在枝干上选一片叶子，从这个叶子的位置到达下一个正对的位置称为一个循回。叶子在一个循回中旋转的圈数也是斐波那契数。

•      再例如，树木的生长，由于新生的枝条，往往需要一段“休息”时间，供自身生长，而后才能萌发新枝。所以，一株树苗在一段间隔，例如一年，以后长出一条新枝；第二年新枝“休息”，老枝依旧萌发；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则次年“休息”。这样，各个年份的枝桠数，便构成斐波那契数列。这个规律，就是生物学上著名的“鲁德维格定律”。（百度百科）

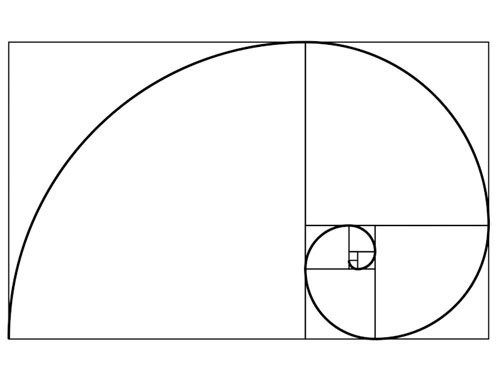
    斐波那契数列在欧美可谓是尽人皆知，于是在电影这种通俗艺术中也时常出现，比如在风靡一时的《达芬奇的密码》里它就作为一个重要的符号和情节线索出现。

    而著名的斐波那契曲线，由于它和黄金分割比例的关系，不但被古典画家用于绘画中，更是被今天的一些画家作为一个绘画门类而进行创作活动。

（待续）