| 781、绝境下的人性·广相论24(曲面微分几何) |
| 送交者: 和颜清心 2019年06月21日06:59:27 于 [教育学术] 发送悄悄话 |
|
《绝境下人性的极致》
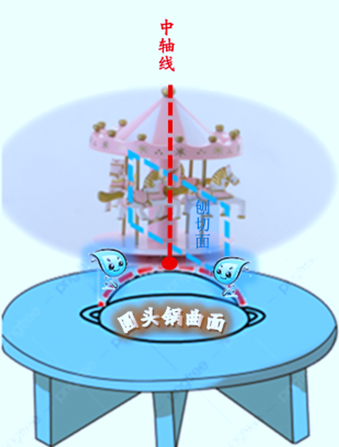
……河水咆哮着,没有过河的筏子, 只有几只黑子父亲自制的葫芦可以帮助渡河。 欧文紧紧抱着年幼的花花, 又用绳子捆着受伤的安洁, 三个人艰难地在水中游着, 安洁不会游泳,又因伤势过重, 已经没有力气,配合欧文往前游了, 安洁看着极度疲劳的欧文, 看到欧文正在拼力地拖着自己往前游, 她本能地拿出匕首割断绳子, 在割绳子的瞬间,她的眼泪流下来……, 她在向欧文告别, 她在祝福欧文平安脱离险境……。 安洁本可以选择不割绳索, 是怎样的勇气、怎样的爱, 能让一个人在那一瞬 断然放弃生命成全他人? 为了不拖累欧文, 她把缠绕在身上的绳索切断, 滔滔河水淹没了她的身躯, 没有一句豪言壮语, 有的只是默默的奉献, 而这一奉献, 正为天地谱写了一曲高尚灵魂的赞歌! 安洁,你是一位天使。 开心(曲面)微分几何 (曲面)微分几何过于抽象, 对初学者来说,如果不详加解释, 形同虚设、等于没学, 这就有点些像我们来到一个国家, 国内所有情景异常枯燥,毫无生气, 除非不得己, 一个正常人是无法在这里活下来的。 话说数学家是如何将弯曲时空的曲率 用到曲面微分几何的呢?下面举例说明。 先看一个栗子,我们知道, 对于曲面上某个切点G, 通过旋转(像旋转木马那样) 可以形成无限多面 (由于纸面限制,图中只出现一个面)。
每个木马经过旋转,可以形成相应的 无限多切面*和无限多切线*。 【注释】 ‘切面’有球切面、圆柱切面和圆锥切面。 下面先解释一下什么叫‘球切面’ 以及什么是‘切点’和‘切线’。 (1)与球面只有一个交点的平面叫‘球切面’。 (2) 球与切面的公共点叫‘切点’。 (3)和球只有一个公共点的直线,叫‘球的切线’。
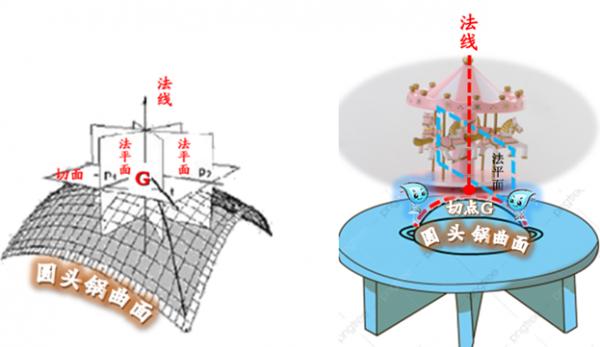
这些切线如果是在‘一个平面’上 (该平面是处在与旋转空间的 ‘竖直线’成90度的位置上), 按照相关定义, 我们称‘这个平面’是这个点的‘切平面’。 傻了吧?再读一遍。再读一遍,仍模糊……, 好了,现在让我们想象有一座 旋转木马, 建筑商(异想天开地)将这旋转木马, 建在一个山包上…… 嘿,等一下,游乐场建在山包上? 谁还敢去啊?那么就换一下, 让我们想象,旋转木马是用生日蛋糕做成的, � 我们可以把它放在一个‘倒扣’的圆锅上, 然后用小刀,把这个蛋糕,从‘中轴线’处, 切成许多份儿,于是会看到每一份儿 都出现了蛋糕的切面, 这种切面也可称‘刨切面’ (如图),
细看这个蛋糕有个特点, 就是它比普通蛋糕含水量多(即松软许多), 蛋糕含有许多水分, 这时如果有个精灵利用魔法, 将蛋糕的水份聚集起来, 那么被聚集的水份, 就会像小瀑布似地 紧贴着圆锅鼓鼓的立体曲面往下流淌(如下图)
待续。谢谢。 |
|
 |
 |
| 实用资讯 | |
|
|
| 一周点击热帖 | 更多>> |
| 一周回复热帖 |
| 历史上的今天:回复热帖 |
| 2018: | 汉武帝的真正贡献是反封建复辟 | |
| 2018: | 对网友老几博 “兔子的范例简介”的简 | |
| 2017: | 活着如何做一个不是恶霸的大地主 (六 | |
| 2017: | 彭运生谈艺录(64) | |
| 2016: | 天下网商前执行主编财经记者胡采苹被曝 | |
| 2016: | 现代城市需要一些湖泊 | |
| 2015: | 范例哲学对量子缠绕现象的解释 | |
| 2015: | 中国现代哲学家学会:再谈范例的分类 | |