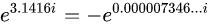| 四色定理、哥德巴赫猜想、费马大定理、黎曼猜想、欧拉公式融入超 |
| 送交者: wxmwrkhp 2019年01月16日17:26:49 于 [教育学术] 发送悄悄话 |
|
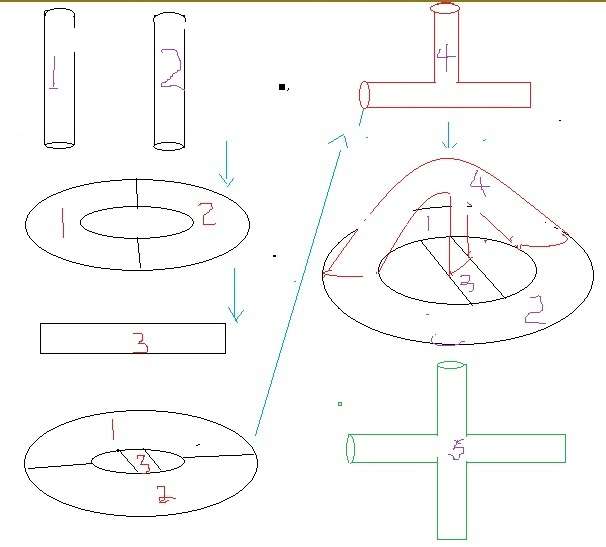
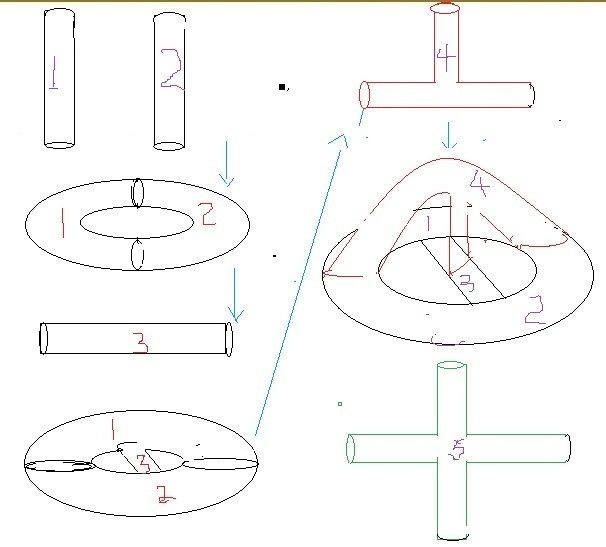
哥德巴赫猜想、费马大定理、黎曼猜想、欧拉公式、m理论大融合62 人赞了该文章 一,前言 大自然的运行有两种模式,一种是由一到多,例如树木由一根主干生长到很多树枝树叶,人类祖先最开始只有亚当和夏娃再到数千人到现在70亿;另一种是由多到一,例如千万的山间小溪汇集江河最后到海,再一个就是人类的知识,由多学科多门类融合到一个总理论。 科学最让人不可思议的是它的融合,无数自然现象可以归结为物理学、化学、生物学、....。 今天的文章注定是一个载入史册,它是人类思维的辉煌壮举,它把数学中最经典的哥德巴赫猜想、费马大定理、黎曼猜想、欧拉公式和广义相对论量子理论的m理论融合在一个模型里。 二,从四色定理开始 法兰西斯·古德里于1831年生于伦敦,在1852年提出的猜想,只需要四种颜色为地图着色。这是因为他发现在平面上或者球面上,只能有4个区域两两相连,英国数学家德摩根证明了平面上不存在5个区域两两相连。 1974年德国的林格和美国的杨斯证明了在曲面上染色定理,例如,在一个汽车轮胎形状的环面需要7种颜色,因为可以构造7个两两相连的区域,6种颜色肯定不够的;在有两个洞的双环面需要8种颜色,因为可以构造8个两两相连的区域,7种颜色肯定不够的;....。 三,数学家证明了可以构造无穷多个两两相连的区域 如果你不能理解,让我慢慢道来: 现在有两根管子,一个记为1,一个记为2,它们代表两个区域。我们假定所有的管子都是可以随意拉伸和弯曲的。 把两根管子端端相连,就是一个汽车轮胎一样的环,它有两个区域,我们再用一根直管子记为3,安在这个环的中间,一头连着区域1,一头连着区域2,现在它是有两个洞的双环了,有三个区域两两相连。 现在我们用一个“丁”字型的三叉管,记为区域4,三个端口分别与区域1,区域2,区域3 相连。于是现在有4个区域两两相连; 我们再用一根四叉管记为区域5,4个端口分别与区域1,2,3,4相连,现在有5个区域两两相连。 这个步骤可以无限制进行下去,用五叉管,六叉管,...。构造无穷多个区域,它们都是两两相连的。 数学家和物理学家把这个叫做岐管。
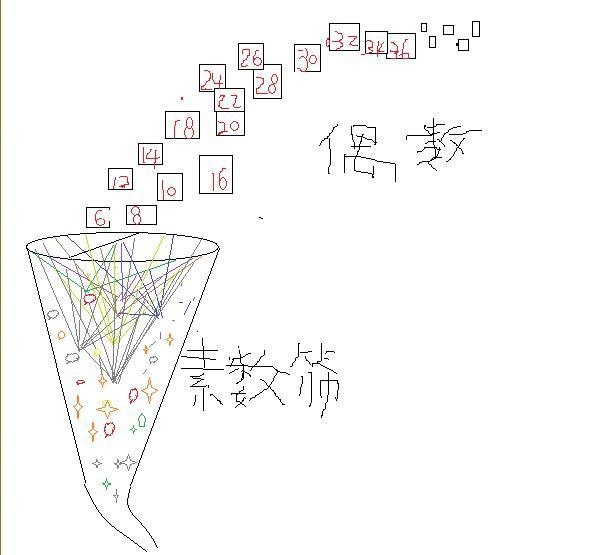
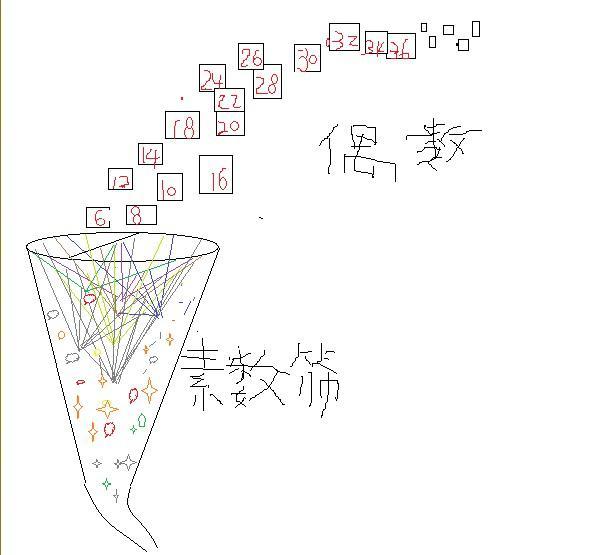
四,数论与图论联系起来 在数论中,最重要的元素就是素数,欧几里得证明了有无穷多个素数,并且它们有一个特点就是两两互素。无穷多个两两互素的素数与无穷多个两两相连区域一一对应。 就是说用这个方法把数论与图论联系起来,这个方法的意图叫做朗兰兹纲领。 区域1,代表第一个素数2,第二个区域代表第二个素数3,...,第n个区域代表第n个素数。 我们把这个岐管倒过来,就像一个网子,篮球网子。篮球网子是把篮球往里面投。 公元前300年古希腊有一个数学家叫做埃拉特斯特尼,他把这个网子当成筛子,把自然数往里面扔,他说凡是合数通过筛子以后就会从网子里面筛掉,留下的是素数,这个就是著名的埃拉特斯特尼筛法。
五,与哥德巴赫猜想联系起来 我们上面这个岐管筛子是把偶数往里面扔,哥德巴赫说,大于4的偶数一个也不会漏出筛子,除了6=3+3以外,其他偶数都是可以在不同的素数区域被拦截。例如8会在区域2也就是素数3和素数5(第三个区域)被拦截;偶数10会在素数3和素数7的两个区域之间被拦截;...。总之,无穷多个偶数都逃不脱这个网子,没有一个偶数可以漏到外面去。 六,哥德巴赫猜想与费马大定理联系起来了 看到没有?数论与图论已经融合一起了。 这个还不算神奇,这个岐管的内部空间我们记为X,外部空间记为Y,它有很多洞,可以有无穷多个洞,可以有无穷多个空间维度n,宇宙内外整体记为1,就是说 Xⁿ+Yⁿ=1,这个叫做费马曲线,它是由费马大定理Aⁿ+Bⁿ=Cⁿ同时除以Cⁿ得到的。 费马大定理与哥德巴赫猜想联系起来了。 七,这个岐管就是m理论的架构 物理学家认为,宇宙是10维空间或者11维空间,或者26维空间等5个版本。还有物理学家认为有无穷多个维度的空间。他们管这个理论叫做玄理论或者M理论,是把广义相对论与量子理论结合一起的终极理论,霍金说是最后的理论。 八,与黎曼猜想联系起来了 数学家考虑的是怎样计算这个岐管上的区域或者计算区域上面的一个点。如果岐管上某一个区域 n,在n上的一个点是1/n,因为这个岐管有无穷多个维度,或者很多维度,我们要定位这个点,就要考虑它的管壁——实部,还有考虑它的内外空间位置——虚部。 所以,这个点
,S=α+βi。 i是虚数,α表示实部,实部当然是1/2,因为这个多维宇宙等于1,岐管属于实部,实部上的点当然是1/2。这个正是黎曼函数黎曼猜想
。物理学里,真空是能量的“零点”。 黎曼猜想与物理学和费马大定理联系起来了。 九,与欧拉公式联系起来了 虚部怎么计算呢?岐管内部看成一个圆管,在岐管上的一个点1/K^S,做一个截面,就是一个圆。大家知道欧拉公式吗?
以e^0=1开始,以相对速度π,走了i时间(参见百度百科“虚时间”),再加1,回到原点。
我们设岐管上的点1/K^S为Δ,那么,e^Δi=-1。 包含了时间(时间有虚的涵义)和空间。 虚时间是为了对应时间起点(大爆炸)而定义的一个概念。在虚时间这个概念体系里,在比三维更高的维度空间,时间并不是一条直线,而是一个闭合的圆,没有起始也没有终结,宇宙的起点如果源自大爆炸,那在此之前的时间将无法定义。因此,为了解决奇点之前时间应该如何,我们引用到了复数的概念。 如果走过头,假如超过了π,走到了3.1416,让我们看一下会发生什么情况: 因为π=3.141592653,所以(1)式:
因为圆周率: π=3.141592653...=3.1416-0.000007346。 所以 (2)式为:
公式(3)可以写成:
我们知道,同底数相除,指数相减 ,反过来也一样,即同底数指数相减,就是两个数相除 公式(4)可以写成:
.........(5) 当大于π时,就是时间走过头了,落入第三象限。欧拉公式是将指数函数e^πi解析延拓到整个复平面上。虚时间就是——(5)式物理学中出现这种情况: 不同时代的人在一个特殊的空间相会,例如今天的人(e^3.1416i)与3000年前的人-e^0.000007346相遇(或者今天的人与未来的人相遇):拿着长矛大刀的古人在与驾驶航空母舰和f—35的带着核弹头的现代人相遇,谁怕谁? 欧拉公式在2011年被评为世界上最美的10个公式之首。 我们的宇宙是由数学最经典的问题和物理学最经典的问题组成的。 与爱因斯坦质能公式联系起来 玄理论认为,从更加宏观角度看,比如亿万年,我们的宇宙就像在一张纸一样薄的膜片上或者肥皂泡膜上,光无法逃逸出膜,被限制在膜上,但是引力可以穿越宇宙的膜向外传播,玄理论的科学假设,宇宙所有的粒子都被局限在一个四维膜的宇宙中,而膜宇宙漂浮在更高维度的体宇宙里,不过,几种特殊的粒子可以从膜宇宙中穿出,其中,最出众的就是引力和惰性中微子。 上面的膜宇宙,对于膜,是一种没有厚度的东西,但是有一个曲面,这是有面积的,设为c,膜包含了质量和能量。E=mc^2。爱因斯坦方程中式中E为能量,m为质量,c为光速。它是一切物质运动速度的最大极限。这个公式就是爱因斯坦质能方程式。在膜宇宙中,光速只能绕着膜运行,膜的表面积就是光速扫过的面积。因此,c^2=E/m。 我们把爱因斯坦方程也引进了。我们生活在费马大定理的宇宙空间,出面旅行(宏观)需要黎曼猜想和欧拉公式计算路程,穿过哥德巴赫猜想的虫洞,才能到达彼岸。 我们生活在高维宇宙的一小片中,大到银河宇宙,小至原子夸克,都是 弦线构成的。 |
|
 | ||||||||
|
 |
| 实用资讯 | |
|
|
| 一周点击热帖 | 更多>> |
| 一周回复热帖 |
| 历史上的今天:回复热帖 |
| 2018: | 參加香港《主權在民》的民主選舉真爽, | |
| 2018: | 关于我们的认知判断 | |
| 2017: | 历史的必然性看叶公好龙 | |
| 2017: | 彭运生:文化沉思录(9) | |
| 2016: | 溪谷闲人:美国简史十二.棉花是国王 | |
| 2016: | 大喜事:证明了假共“让利台湾”以金钱 | |
| 2014: | 初等教育的怪胎﹕高考最牛班 | |
| 2014: | 七律:无题(新韵) | |






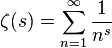
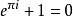
 ......(1)。
......(1)。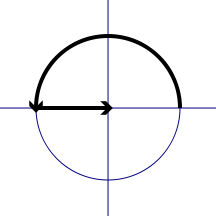

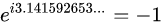
 .......(2)
.......(2)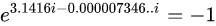
 .......(3)
.......(3)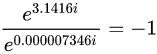
 ........(4)
........(4)