| 走近量子(10)最後的判決 |
| 送交者: 天蓉 2012年02月16日15:10:49 於 [教育學術] 發送悄悄話 |
|
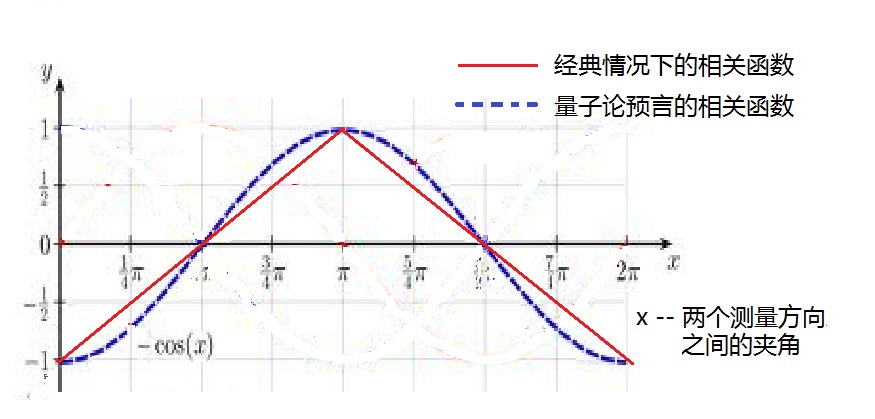
話說當年,因為克勞瑟的寬闊胸懷,也因為他了解到波士頓的3個人已經開始計劃真正的實驗,因此他自己也迫不及待地想加入其中。最後,有關改良和驗證貝爾不等式的這篇論文,以四位物理學家(CHSH)共同署名,發表在1969年的“Physics Review Letter”上。論文中改良了貝爾不等式,取消了幾個關鍵的限制條件,並且重新設計了切實可行的實驗方案。 我們再次把貝爾不等式寫在這兒,以便大家思考∶ |Pxz-Pzy| ≤ 1+Pxy。 這個式子中,有哪幾個關鍵的限制條件需要改進呢?首先,上面的不等式中,有三個測量方向x、y、z。這三個方向是測量兩個互為糾纏的粒子時共用的。而我們又希望在測量的時候,兩個糾纏粒子分開得越遠越好。遠到一定距 就不太容易保證兩邊用的是同一個坐標系了。不是嗎?讓一對雙胞胎遠隔天邊,他們就沒辦法互相丟眼色、弄虛作假啦。但是,兩地 得這厶遠,總不能還使用同一套測謊儀,在兩地之間運來運去吧。另外,貝爾在證明貝爾不等式時用的假設是自旋單態的完備相關,兩個糾纏粒子需要準確地反向飛行。這些條件在真實的實驗中也是不可能完全滿足的。因此,CHSH的文章取消了Bell不等式需要的這些限制,重新推導出一個CHSH-Bell不等式∶ |P(a1,b1)+P(a1,b2)+P(a2,b1)−P(a2,b2)|≤2。 這兒的P(ai,bj)表示相應的相關函數,在實驗ai、bj中的統計平均值。 這個新不等式的相關實驗,不像原來貝爾不等式那樣難以實現了。改良推廣了的不等式中,一對變量,也就是測量的方向(a1,a2),可以在一個子系統上由愛麗絲完成,而另一對變量 (b1,b2)的 測量,在另一個子系統上由鮑勃完成。理論上說,這兩個子系統可以位於空間分 相隔很遠的地點。如果在以上的CHSH不等式中,假設體系總自旋為零,並且選取特殊情況的a1=b1,以及使用理想的反向關聯函數∶P(b1,b1)=-1, CHSH不等式就化簡為原版的Bell不等式。 在CHSH論文中的後半部分,作者提到用‘原子級聯’的方法來生成驗證Bell-CHSH不等式的糾纏光子對,而不是用吳健雄那種正負電子對湮滅的方法。‘原子級聯’的實驗幾年前曾經由加州柏克萊大學的科協爾和康明斯兩人做過,並且也曾經測量過相關函數。但他們的測量數不足以用來證明貝爾不等式,因為他們只測量了交角為0度和90度時候的相關函數值。而從我們在第7、8節導出貝爾不等式時就知道,根量子力學,夾角為θ的兩個不同方向上糾纏態粒子的關聯函數平均值是(-cosθ)。因此,在0度、90度、180度等角度時的相關函數值,或者是-1,1,或者是0。在這些平凡情況下,量子論和經典論沒有差別(見下圖)。如下圖中的紅藍兩條曲線所示,經典理論和量子論預言的相關函數之差別很小,並且是在兩個觀測方向的夾角在0度和90度之間的那些角度,貝爾定理的實驗驗證,就是要測量出藍色虛線相對於紅色實線數值之差。
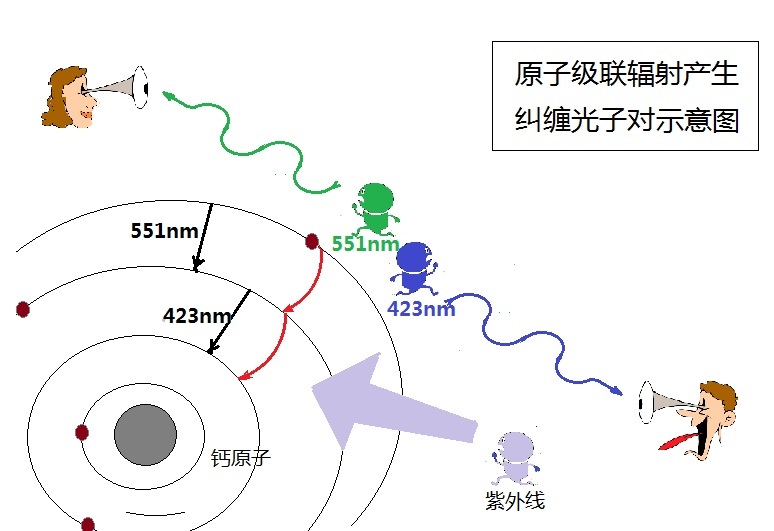
在此也簡單說明一下所謂‘原子級聯’躍遷產生糾纏光子對的方法∶比如,如下圖所示,一個鈣原子中的電子被紫外線襲擊,有可能被激勵到高出2個能級的狀態。然後,當能量回落時,就有可能連續下降兩個能級而輻射出兩個糾纏的光子(在鈣原子的例子中,將輻射出波長分別為551nm的綠光光子和423nm的藍光光子)。
需要提醒讀者注意的是,上面的示意圖中,我們只畫出了一個鈣原子、一個紫外線光子,激發一個電子,產生一對糾纏光子。這顯然不是實驗中的真實情況。實際上是一束紫外線打到一堆鈣原子上,輻射出來的也是兩束光,很多對糾纏光子。在測量相關函數時,需要對多個光子運用統計方法進行計算。以後談到實驗時,也都是說的這種統計的測量和計算效應,特此表明,不再贅述。
無論如何,克勞瑟發現,要證明貝爾不等式,柏克萊大學科協爾和康明斯的實驗數還不足夠,但是他們的方法卻是非常可取的。於是,克勞瑟心急如火,想儘快做出這個實驗,便立刻寫信給他的祖師爺湯斯,申請柏克萊大學博士後的工作。他如願以償,湯斯接受他做博士後,進行有關射電天文學的觀測研究。湯斯畢竟是得過諾貝爾獎的大師級人物,眼光不凡,遠見卓識,還同意克勞瑟在做射電天文的同時,分出一半時間來做驗證貝爾不等式的量子力學實驗。不過,當克勞瑟到達柏克萊時,科協爾已經 開,康明斯還在那兒。但是,康明斯對驗證貝爾不等式之事不感興趣。最後,還是由湯斯出面,提議康明斯讓一個研究生幫助克勞瑟工作。這樣,克勞瑟才和Freedman一起,開始了他的實驗。
如此一來,原來的四人小組CHSH在進行實驗時,開始分道揚鑣了∶克勞瑟和Freedman在美國加州柏克萊大學實驗室,背後有西摩尼和霍恩的支持。而哈佛的霍爾特,則從‘四人小組’中脫身出來,繼續在波士頓的哈佛進行自己的實驗,作為他PHD博士論文的課題。天下之事,分久必合,合久必分,科學家們之間也是如此。於是,這四個原來的合作夥伴,分別在美國東西兩岸拉起隊伍,暗暗地展開了競爭。
這四個人又如何預料和期待他們的實驗結果呢?
克勞瑟是一個熱情洋溢、活潑外向的年輕人。和貝爾一樣,更相信愛因斯坦的隱變量解釋,非常希望自己實驗的結果能有助於找出量子論中的隱變量,引起物理理論的大革命。他用當時看起來數目不小的一筆錢(說是500美元)與一個朋友打賭,賭隱變量理論贏,量子力學輸。霍恩沒有和人打賭,但認為量子力學會贏,因為他覺得這個古怪的量子力學總是贏!老練的西摩尼則不表態,說只能讓實驗結果說的話才算數。在哈佛大學單槍匹馬戰鬥的霍爾特,則認同哈佛當時大多數物理學家相信的正統觀點,希望自己的實驗結果能成為量子力學完備性強有力的證明。
1972年,克勞瑟和Freedman發表了他們用兩百多個小時完成的實驗,這實驗之所以如此費時,也是因為當時的實驗條件下,得到糾纏態粒子對太困難的緣故。那真的是百丌里挑一的幾率∶每100丌對光子中,可能只有一對,是能夠成功地被觀測到,對結果作出貢獻的糾纏光子對。這點毛病不但拖長了實驗的時間,也影響了實驗的精度,被後來的實驗者稱之為“偵測漏洞”而提出質疑並加以改進。
有趣的是,這兩個實驗的結果,都和實驗者的期待相反。克勞瑟希望量子力學輸,他的實驗結果卻大大地違背貝爾不等式,以5倍於誤差範圍的偏 ,強有力地證明了量子力學的正確!
幾乎同時,霍爾特也得出了他的實驗結果,但他保持沉默不作聲,遲遲沒有發布他的結果。他的結果與他的期待不一樣,沒有違背CHSH-貝爾不等式,好像是支持隱變量理論的,這令相信量子論的霍爾特心中忐忑不安。當然,使得霍爾特猶豫不言的主要原因,是因為他的實驗結果看起來非常勉強。在上面的CHSH-貝爾不等式中,不是要求兩地所測的四個關聯函數之和≤2嗎?而霍爾特的結果小於2,又很靠近2。因此,他相信實驗中一定有什厶地方不對頭,影響了觀測結果。霍爾特的實驗也是使用原子級聯的方法來產生糾纏光子,但是,他不是用鈣原子,而是使用汞。後來,有人找出了他實驗中的問題,重新用汞做了這個實驗,仍然得到了支持量子論的結果。
之後,接連又有好幾個實驗小組,包括吳健雄的實驗室在內,都進行了檢驗貝爾不等式的實驗,結果全都證明了量子力學的正確性。
不過,大家公認的對量子力學非定域性的最後實驗判決,卻是到了80年代初,由一位法國物理學家阿斯派克特作出的。
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | 《安徽商報》:“肖氏手術”5患者起訴 | |
| 2011: | 霍夫”圓柱對稱引力波”在物理上之不成 | |
| 2010: | 再談“上帝長啥樣”和科學與宗教對提問 | |
| 2010: | 宵寒:人創造了上帝 | |
| 2009: | 回應一目:談談基督教的奴性 | |
| 2009: | 職老:也談談所謂的微進化--駁斥真話不 | |
| 2008: | 追憶西南聯大:最好的時光 | |
| 2008: | 最近的中醫藥討論 | |
| 2007: | 清華和交大幾個大的核心學科群個人所感 | |
| 2007: | 丘成桐的騙局大白於天下 | |