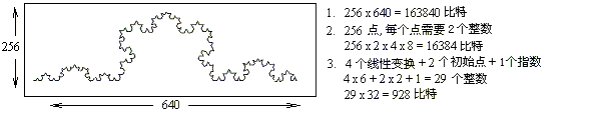| 天蓉:《走近混沌》-10-簡單之美 |
| 送交者: 天蓉 2012年09月13日13:04:42 於 [教育學術] 發送悄悄話 |
|
第十章:簡單之美
儘管幾個簡單的線性自相似的經典分形的歷史,最早可追溯到十九世紀後期。但對於分形的深入研究,諸如曼德勃羅圖等,卻是近四十年的事。這是與計算機的飛速發展分不開的。因為,先進快速的計算技術使得大量的迭代運算可以在更短的時間內完成。圖象顯示技術的發展為我們提供了探索分形複雜性的方便環境。沒有現代的計算機技術,人們不可能欣賞到如此美麗的曼德勃羅圖和朱利亞圖。 “從藝術的角度,非線性迭代生成的分形圖案的確很美。”李四說∶“那種美給我們以視覺的享受,分形音樂則給我們以聽覺的享受。但是,科學家們所欣賞的應該是另一種美┅┅”
“對呀!是這個世界所遵循的科學規律的內在之美。”王二搶着補充了幾句∶
“你們還記得吧,用計算機生成的樹葉圖和瞢類植物葉子是如此之相像,還有樹枝、腦血管、人體┅┅這段時間我一直在想,世界上這些看起來千變丌化的一切,恐怕都是由幾條簡單的生成規則演化出來的哦,就像張三在計算機程序中用一個簡單方程進行迭代一樣,細胞分裂又分裂,迭代又迭代,一代又一代┅┅最後就成了我們世界中的各種生物體。啊,不只是生物,還有雲彩、閃電、海岸線┅┅幾條簡單規律產生了大自然的一切┅┅”
看着王二浮想聯翩的神態,張三笑了∶“別想象得太遠了!想我們力所能及的。你剛才說到的樹葉圖和瞢類葉子相像這點,使我想起最近看到的一篇文章,談到將分形用在計算機圖像壓縮技術方面的事情。”
計算機技術使得我們能探索分形的複雜性,分形數學又反過來造福於計算機技術。科學和技術總是相輔相成,互相推波助瀾。科學始於探索,技術立足於應用。探索能發現自然之美,應用則創造人工之巧。美之事物必能找到應用的途徑,而新穎的技術腹思又總是能反射出理論的光輝。分形之美與電腦顯示技術之新成果息息相關,相照輝映。
當年,分形的研究之所以能在眾多的學科範圍內引起轟動,其原因之一便是∶如此複雜的結腹卻產生於幾條簡單的變換規則。複雜是一種美,簡單也是一種美。科學的宗旨之一可以說就是要用簡單的規律來描述複雜的大自然。複雜的形態背後可能隱藏着簡單的法則。
從分形的這種‘簡單表示複雜’的特性,人們很自然地想到了將分形用於作為計算機中儲存、壓縮圖形資料的一種方式。比如象曼德勃羅集那樣複雜的圖形,只不過是用一個簡單的方程(z = z*z + c)就能表示出來。今天,我們的的文明社會正在大闊步地邁進一個數字信息時代。數字化之後的信息需要通過媒介來記錄、傳送、儲存。使用傳統的方法儲存聲音和圖像,數量非常大。因此,我們才有了所謂的圖像壓縮技術,就是要在保證一定質量的條件下,將儲存的信息量減少,減到越少越好。
那厶,有哪些傳統的圖像儲存和壓縮方法呢?
在數字世界中,信息量的多少用所需要的比特數(0或1)來衡量。表達信息時所需要的比特數目越小越好。也就是說,最好能將信息“壓縮”一下。也叫做給信息“編碼”。比如說吧,為了要儲存下圖中的只有黑白顏色的科赫曲線,我們可以採取如下右邊的文字說明中所列舉的三種方法編碼∶
圖(10.1)∶用不同方法壓縮圖象的說明
第一種是最原始的方法,是將圖形分成許多小格子(象素)。例如,我們可以將圖(10.1)分成 256*640個小格子,也就是共163840個象素。然後,需要將這些象素所具有的信息儲存起來。因為圖(10.1)只是黑白圖形,每一個象素的信息不是‘黑’,就是‘白’,正好對應於比特的‘0’或‘1’。這意味着,一個象素需要一個比特來表示。因此,要用這種編碼方法儲存整個圖形,需要的比特數就等於163840。第二種方法是將圖形看作諾干點和線。上面的圖中共有256條直線,經由256個點逐次連成。所以,只要儲存這256個點的位置就可以了。因為每個點在圖中的位置需要兩個整數表示,而每個整數都需要32個比特來表示。因此,這第二種編碼方法需要的比特數是256*2*32=16384。顯然,第二種方法比第一種方法更經濟合算,因為它將信息壓縮了10倍。
如果我們把這個圖形用它的分形的初始值及迭代函數來編碼的話,就是上圖中的第三種方法。使用第三種方法,需要儲存的信息只包括4次線性變換迭代以及2個初始點位置。將這些數值換算成比特數,只需要928個比特就可以了。比較原始的163840比特而言,就等於信息被壓縮了100倍以上。
有關分形技術用於圖像壓縮,張三談起了他自己的經驗∶在儲存曼德勃羅集圖形時,如果存為(BMP)文件的話,文件的大小為430*8千比特,這種方法就相當於上面所說的第一種方法。而如果將它存為(GIF)文件的話,文件的大小僅為30*8千比特。也就是說,在這種情形下,gif格式相對於bmp格式,信息壓縮了14.3倍。
張三說∶“可是gif格式也太大了啊,我用程序生成這個圖形,存的信息不過是一個簡單方程,幾個係數,就像剛才的科赫曲線,最多幾個千比特,就足夠了呀。”
王二又興奮起來∶“對啦,生物體一定是把某種類似的、最優化的編碼存到基因,DNA裡面了┅┅大自然往往做得比人工更為精緻和巧妙┅┅”
李四卻很感興趣分形圖像壓縮,說是曾經做過用傅立葉變換壓縮聲音信號的問題,先和兩位一起複習複習。
張三附合∶“對,我們先不管圖像信號,聲音信號的處理更基本和簡單一些。”
其實,不論是聲音還是圖像信號,最原始的信息都可看作是強度關於時間(或空間)的函數。如我們上面說到的,一個固定的黑白圖像可用在每一個像素位置的光強度(0或1)表示,一個原始的聲音信息則用在一系列的時間點測量的聲音強度來表示。所以,最原始的儲存方法就是∶把聲音的強度按不同時間點列成一個表儲存起來,比如說,轉換成電信號保存到磁帶上。以後便可以將磁帶上的數值讀出來,再轉換成聲音信號。
這種儲存聲音的原始方法類似於剛才談到圖像編碼的第一種方法。可以說是完整的儲存方法,但它並不總是最好的,也不是最有效的方法。
聲音的信號除了隨時間而變的強弱之外,還有一個很重要的特點,就是它的頻率。頻率也是聲波中給我們大腦更深刻印象的東西。學唱歌時首先不就是學“多來米法碩”嗎,那描述的就是聲音中不同的主頻率。
剛說到“多來米法碩”,正好林零和一夥音樂系的女學生在旁邊走過,聽見這句話便好奇地站下來繼續聽。
既然頻率在聲音中是如此重要,人們自然想到儲存聲音應該儲存它的頻率。對啦,作曲家們就很聰明,他們將所作的曲子用樂譜的形式記下來,那不就是記錄的頻率嗎?傅立葉變換呢,則是科學家工程師們所使用的樂譜,是由法國數學家在1822年創立的。比之音樂中的樂譜,傅立葉頻譜有過之而無不及,它把聲音信息中包含的所有頻率分量都找了出來。這個過程聽起來有點繁瑣,似乎畫蛇添足!不過,傅立葉變換在數學、物理、工程各方面都得到廣泛應用,是信息處理中使用得最多的變換,被譽為信息處理技術上一個重要的里程碑。
儲存頻譜的優點是儲存的信息量少。當我們按下電子琴的中心C按鍵時,電子琴發出一個‘多’的聲音。將這個聲音用強度時間表來儲存,每1毫秒存一個強度值,1分中就需要存60000個實數,需用3840千比特。如果存它的頻譜,暫時不考慮泛音的話,只需要存這個頻率的數值和強度,2個實數就可以了,這不就等於是把信息量“壓縮”了幾千倍嗎?即使考慮還得存泛音的數,也可以達到幾百倍的壓縮率吧。
一個女孩有些迷惑不解∶“一個‘多’彈一分鐘,這厶長啊?”
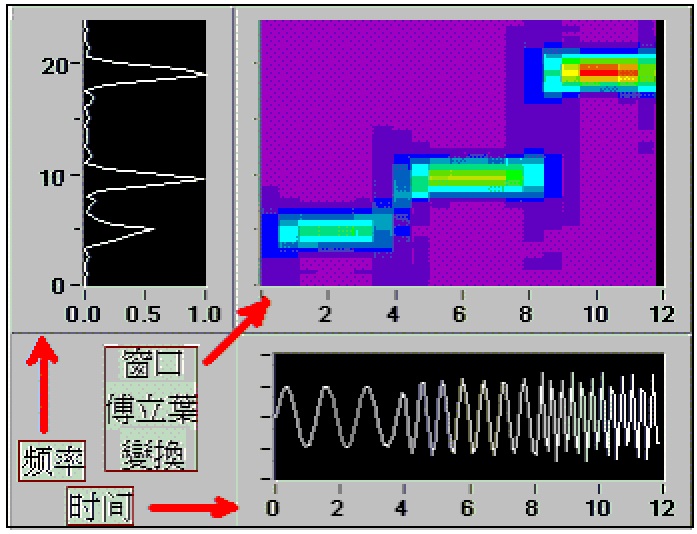
大家笑了起來,笑得女孩有些不好意思。可李四說,這個疑問問到了點子上哦!傅立葉變換隻記下了頻率信號,完全沒有時間的信息,是不行的。它就像是用一把頻率固定、但時間無限長的尺子來量東西,這把尺太長了!所以,在實際上使用的是如圖(10.2)所示的‘窗口傅立葉變換’,把尺子按時間分成一段一段的。
圖(10.2)對三段不同頻率的正弦函數組成的圖形的窗口傅立葉變換結果
林零很有悟性,對王二說∶“這個窗口傅立葉變換的道理和音樂上的曲譜很像啊。既有時間,也有頻率┅┅但是┅┅這些和你們談論的分形又有什厶關係呢?”
王二向她解釋了一下剛才談到的分形用於圖像壓縮之事。
剛才說到的是對聲音信息的傅立葉變換處理。回到圖像編碼領域,原理也是類似的,只不過需要將時間用二維空間來代替。
對信號的傅立葉變換壓縮,利用的是信號的頻率特徵。用分形的原理進行圖像壓縮,則是利用圖形的自相似性。
分形圖象壓縮的方法(也稱迭代函數系統IFS方法)是美國佐治亞理工學院的巴恩斯利教授首創的。但分形圖像壓縮技術至今仍然不夠成熟。儘管目前已有商品化的計算機軟件,但仍有許多問題尚待解決。分形圖像壓縮的解碼速度很快,但編碼速度慢,比較 合一次寫入、多次讀出的文檔。
正是∶“路漫漫其修遠兮,吾將上下而求索。”
上一篇∶分形音樂 下一篇∶ |
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | 我對林彪將軍的評價(原創) | |
| 2011: | 文革巨大科研成就的必然性分析 | |
| 2010: | 鄒容:革命必剖清人種 | |
| 2010: | 現代京劇《洋涇浜-智斗》 | |
| 2009: | 回基甸-上帝正在愛你,而你不知感恩 | |
| 2009: | 國家發展水平,教育背景同宗教之間的關 | |
| 2008: | 在聽施一公的講座,很感動(ZT) | |
| 2008: | 襄汾潰壩、三鹿毒奶如何讓官員舉一反三 | |