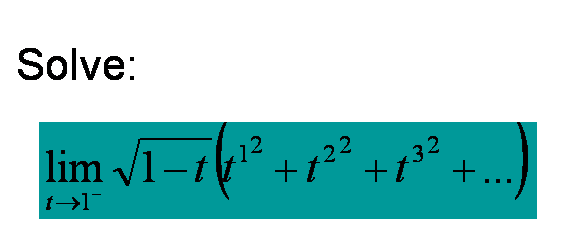一年級極限數學題比較細膩的解答(改錯重貼)-靈機一動-萬維論壇-萬維讀者網（電腦版）

送交者: 粱遠聲 2016年01月03日08:25:37 於 [靈機一動] 發送悄悄話

一年級極限數學題討論解稍嫌粗糙

我曾這樣解過這道題：
求：
lim(t->1-) sqrt(1-t)(t^(1^2) + t^(2^2) + t^(3^2) + ... + t^(n^2) + ...)
令 dx = sqrt(1-t)
t = 1 - dx^2
原式 = sqrt(1-t)(t^(1^2) + t^(2^2) + t^(3^2) + ... + t^(n^2) + ...) =
dx( (1 - dx^2)^(1^2) + (1 - dx^2)^(2^2) + (1 - dx^2)^(3^2) + ... + (1 - dx^2)^(n^2) + ...) =
dx( [(1 - dx^2)^(1/dx^2)]^(dx^2)] + [(1 - dx^2)^(1/dx^2)]^((2dx)^2) +
[(1 - dx^2)^(1/dx^2)]^((3dx)^2) + ... + [(1 - dx^2)^(1/dx^2)]^((ndx)^2) + ... )
因為[(1 - dx^2)^(1/dx^2)] -> e^(-1)
原式可近似寫成
原式 = (e^( -dx^2) + e^(-(2dx)^2) + e^(-(3dx)^2) + e^(-(ndx)^2) + ...)dx
讓dx趨近於0,
上式 -> Int(0,inf)[e^(-x^2)dx]
做到這裡，稍嫌粗糙。嚴格的做法是證明
當k = 1,2,3...,n 時，
e^(-((k+1)dx)^2) < (1 - dx^2)^(k^2) < e^(-(kdx)^2)

根據不等式 1 - x < e^(-x), 很容易證明 (1 - dx^2)^(k^2) < e^(-(kdx)^2)
要想證明 e^(-((k+1)dx)^2) < (1 - dx^2)^(k^2)，只需證明
e^(-((1+1/k)dx)^2) < 1 - dx^2 (1)
令 y = 1 - x^2 - e^(-(1+1/k)^2 x^2)
y(0) = 0
dy/dx = 2x((1+1/k)^2 e^(-(1+1/k)^2 x^2) - 1)
如果找到x的區間使得dy/dx > 0。這個區間也是(1)成立的區間。問題歸結為，找到x的區間使得

e^(-(1+1/k)^2 x^2) < (1+1/k)^2
令 x = d/n。問題歸結為，找到d的區間使得
e^(-(1+1/k)^2 (d/n)^2) < (1+1/k)^2
d^2 < (2n^2/k)ln(1+1/k)^k/(1+1/k)^2
因為ln(1+1/k)^k單調增加，(1+1/k)^2單調減少，
Min ln(1+1/k)^k/(1+1/k)^2 = ln(2)/4
當 d^2 < 2nln(2)/4 時， (1)成立。
取 d = sqrt(n)/2; dx = d/n; lim(n->inf)dx = 0; lim(n->inf)d = inf,
我們有
e^(-((k+1)dx)^2) < (1 - dx^2)^(k^2) < e^(-(kdx)^2)
令
f(n) = ( (1 - dx^2)^(1^2) + (1 - dx^2)^(2^2) + ... + (1 - dx^2)^(n^2))dx
p(n) = (e^( -dx^2) + e^(-(2dx)^2) + ... + e^(-(ndx)^2))dx
g(n) = (e^( -2dx^2) + e^(-(2dx)^2) + ... + e^(-((n+1)dx)^2))dx
得到
g(n) < f(n) < p(n)
因p(n), g(n)趨近於同一極限Int(0,inf)[e^(-x^2)dx]
所以
f(n) 趨近於 Int(0,inf)[e^(-x^2)dx]

0%(0)

	實用資訊

回國機票$360起 | 商務艙省$200 | 全球最佳航空公司出爐：海航獲五星
海外華人福利！在線看陳建斌《三叉戟》熱血歸回豪情築夢 高清免費看無地區限制

一周點擊熱帖

更多>>

一周回復熱帖

歷史上的今天：回復熱帖

2014:	稱12個小球的修改版
2013:	范兒98——美人計（中共）：恆心與自律
2011:	Eat in and Take out 有誰比我譯得還好