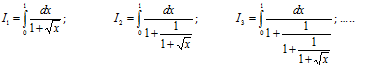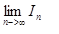| 又見兔子 |
| 送交者: 零加一中 2017年08月06日06:27:28 於 [靈機一動] 發送悄悄話 |
|
定義:
求
We first introduce Fibonacci numbers. f(0) = f(1) = 1, f(n) = f(n-1) + f(n-2), n ≥ 2. In integral I(n), let x = y*y. It is not hard to prove that the integrand is 2y {[f(n-1) + f(n-2)y]/[f(n) + f(n-1)y]} ≡ 2y g(n, y). We will omit y inside g(n, y) as g(n). Fibonacci number f(n) has the asymptotic form sqrt(5)/x0^n where x0 is the Golden Ratio 0.618… Using this asymptotic form, after simplification, g(n) ≈ x0 I(n) ≈ x0 = [sqrt(5) – 1]/2. |
|
|
 | ||
|
 |
| 實用資訊 | |