一年級極限數學題討論解稍嫌粗糙

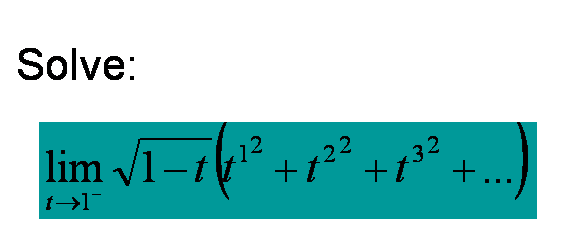
求：
lim(t->1-) sqrt(1-t)(t^(1^2) + t^(2^2) + t^(3^2) + ... +  t^(n^2)  + ...)

令 dx = sqrt(1-t)
t = 1 - dx^2

原式 = sqrt(1-t)(t^(1^2) + t^(2^2) + t^(3^2) + ... +  t^(n^2)  + ...) =
dx( (1 - dx^2)^(1^2) + (1 - dx^2)^(2^2) + (1 - dx^2)^(3^2) + ... +  (1 - dx^2)^(n^2) + ...) =
dx( [(1 - dx^2)^(1/dx^2)]^(dx^2)] + [(1 - dx^2)^(1/dx^2)]^((2dx)^2) +
    [(1 - dx^2)^(1/dx^2)]^((3dx)^2) + ... + [(1 - dx^2)^(1/dx^2)]^((ndx)^2) + ... )

因為[(1 - dx^2)^(1/dx^2)] -> e^(-1)

原式可近似寫成

原式 = (e^( -dx^2) + e^(-(2dx)^2) + e^(-(3dx)^2) + e^(-(ndx)^2) + ...)dx

做到這裡，稍嫌粗糙。嚴格的做法是證明

e^(-((n+1)dx)^2) < (1 - dx^2)^(n^2) < e^(-(ndx)^2)

應用介值定理得到

(1 - dx^2)^(n^2) =  e^(-((n+qn)dx)^2)
0 < qn < 1

代人原式得

原式 = (e^(-((1+q1)dx)^2) + e^(-((2+q2)dx)^2) + e^(-((3+q3)dx)^2) + e^(-((n+qn)dx)^2) + ...)dx

讓dx趨近於0,

原式 -> Int(0,inf)[e^(-x^2)dx]

那麼怎樣證明

e^(-((n+1)dx)^2) < (1 - dx^2)^(n^2) < e^(-(ndx)^2)

又能使滿足這樣不等式的dx 使得ndx充分大呢？