| 在高空客機上能感覺到地球地平線的弧度麼? |
| 送交者: 高玉寶 2018年07月15日12:28:41 於 [五 味 齋] 發送悄悄話 |
|
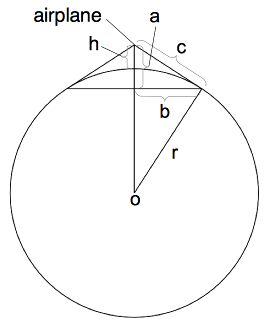
現在竟然還有人相信地平說,覺得有點不可思議。有人推銷地平說,我不覺得奇怪,因為推銷雜七雜八東西的大有人在,如這個教那個功、這個大師那個神醫的,五花八門不在少數。我奇怪的是竟然會有好多人會接受地平說。地平主義者的一個論點,就是說要是地球(當然有的語言中,如英語,地球的名字中不帶球)是個球,那怎麼在飛機上看地平線,地平線不是弧形的?當然去跟地平主義者認真辯論是毫無意義的,但我覺得為什麼在飛機上看,地平線不是弧形的這個問題倒還是有點興趣的。其實這個問題,我自己也曾想過,但沒有認真去考慮。我的結論就是飛機高度不夠,人們覺察不到地平線的弧度。前兩天有網友也提了這個問題,我建議可以計算一下,看在空中的飛機上看地平線,弧度有多大,我們能不能覺察出來。 今天吃過午飯後沒事幹,我就想何不就來算一下呢?下面圖中,那個圓代表地球(通過地心的截面,假定地球是個正圓球)。字母o代表地心,r代表地球的平均半經(r = 6371公里),h代表客機飛行高度(不成比例),b則為從飛機上看到的地平線所組成的圓行地面的半經。
假定 h = 12 公里(一般大型客機的飛行高度),那麼我們可以得出(精確到米): c = sqrt((r+h)^2 - r^2) = sqrt((6371+12)^2 - 6371^2) = 391.213公里 b = c * r / (r + h) = 391.213 * 6371 / (6371 + 12) = 390.478 公里 a = sqrt(c^2 – b^2) = sqrt(391.213^2 – 390.478^2) = 23.970 公里 就是說,在12公里高空看到的地平線,就相當於在一個半徑為390.478公里的圓盤中心上空23.970公里的高度看這圓盤的邊緣。那麼這圓盤的邊緣在我們的眼裡,弧度究竟有多大呢?這個可以根據我們的視野角度計算出一定跨度的弧線的高度來表達,即一弧線最高處與連接此弧線兩端的直線(弦)的距離。比如,跨度10厘米、高度一毫米的一根弧線,我們基本上是感覺不到這弧度的(除非有弦在供參照)。但我在這裡不給出具體的計算(誰感興趣可以試試),只是給出一個大家可以體驗的實感方法。 上面這個計算結果意味着,在12公里的高空的飛機上看地平線,就相當於一個身高1.8米的人站在半徑為29米的圓盤中心,看這圓盤的邊緣。也相當於你在一個直徑為2米的圓桌邊緣,眼睛在離桌面12厘米的上方看圓桌正對面的邊緣(也就是在圓桌中心上方6厘米處看圓桌邊緣)。 如你有其它直徑的圓平面的物體,你可以用下面方法體驗。 y = 23.970 / 390.478 = 0.0614 用0.0614乘上此物體的直徑,得到的數字就是你眼睛在此物體邊緣上方的高度,看正對面的邊緣。 當然在高空飛機上看地平線,地平線不會象物體邊緣那麼清晰明了,所以更不易看出弧度。當然我也忽略了光線在接近地面處的可能折射。另外得指出的是,我這並不是證明了地球是個球體,而只是回答了如地球是個球體,我們在飛機上看地平線,能否覺察到弧度的問題。 |
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2017: | 人生自古誰無死,留取丹心照汗青 | |
| 2017: | 小川會俄律師,更多出席者信息曝光 | |
| 2016: | 1987年聯合國投票承認南沙島礁屬於中國 | |
| 2016: | 呵呵。支那人載歌載舞,一如當年911 | |
| 2015: | 給你們講一講老北京,東富西貴,南窮北賤 | |
| 2015: | 我懷疑我老婆公司的女老闆是不是對她有 | |
| 2014: | 俺又多管一哈闲事,替俺闺 | |
| 2014: | 中共太狡猾了。美國一開罵,中共立即將 | |
| 2013: | Zimmerman: 無罪還是有罪? | |
| 2013: | 依法治國是個悲慘世界, | |