有地平主義者問,工程師在設計長橋時,是怎樣考慮地“球”表面弧度問題的,認為如地球是個球的話,設計象中國膠州灣大橋那樣長的橋,地表曲率應該無法忽略。(見這鏈接:國內的正好。不是中國造了世上最長的跨海大橋了嗎,)。我跟貼講,一般情況下地球弧度可以忽略。有地平主義者不服,開始信口開河胡扯起來。見下面截圖。(鏈接在此:別和傻子扯了。)
那麼24英里長的距離,地球弧線與直線間究竟有多大區別呢?此地平主義者說很簡單的計算,可就是很簡單的計算,他也懶得算。那麼我在此就來幫他計算一下。
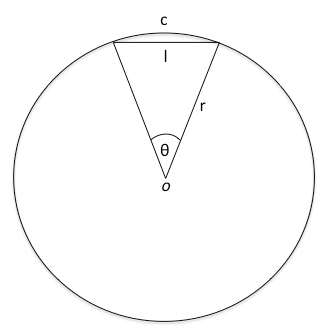
根據地球主義的理論,地球半徑r=6378公里。下圖為經過球心的地球截面示意圖。圖中c代表相對於直線l的弧線,r為地球半徑,θ為c的跨度,。24英里約等於38公里。那麼如c=38公里,l=?
θ= 2πc/(2rπ) = c/r = 38/6378 = 0.0059579805
l = sin(θ/2)2r = sin(0.0059579805/2)*2*6378 = 37.9999415892
38 - 37.9999415892 = 0.0000584108公里 = 0.0584米 = 6 厘米
38公里長的橋,這幾厘米的誤差不可以忽略麼?(如以l=38公里來計算c,這可以作為給夭夭的附加題。)地平主義者的論點基本都是信口開河講的。如還有如地球是個球,那在飛機上看地平線應該看到弧度的論點,也完全只是憑空想象。對這我也作了計算,證明了在一般民航客機上看地平線,是難以覺察到地平線的弧度的。(見鏈接:在高空客機上能感覺到地球地平線的弧度麼?)
很搞笑的是,地平主義者為了證明地球是平的,竟然還用基於地球是個球的原理製造的儀器來測量距離。







