悖论解析 0说明 悖论的本质是语言的“二个真值”的混淆问题。既,两个不同语言层次分别的陈述句所赋真值,自相矛盾。这两个被赋真值的语言层次是:1)陈述句层次,2)元语言层次。悖论的起因是人类从有文明史以来,典型例子是从亚里士多德从语言中发现逻辑开始,二千五百年一直将两个不同层次的语言表达相混淆。悖论的来源,比如,飞失不动,龟兔赛跑,理发师悖论等,从古希腊哲学家芝诺到近代的康托尔/罗素悖论等有许多,它们都可以归结为是两个不同对象,阶段,概念等的,“二个逻辑真值混淆”,所造成。下面以两例说明。
一定义 I:"陈述赋值",P
II:"元语言赋值", Q
二解释之一 1)“我说假话”悖论 1)如果此句,"我说假话", 真的是假话,那么此言为真。但此话告诉我们这句话是假话。所以悖论形成。 2)如果此句,"我说假话", 实际上是真话,那么此言为假。但此话告诉我们这句话是真话。所以悖论仍然成立。 三分析 "我说假话",是对陈述句本身的"赋值,P"。而对上面这整句话赋值,既,"上面话为假或真", 属于对"元语言赋值",Q。元语言赋值,属于"再次对陈述赋值的赋值", 它可以用贝尔二值逻辑导出。
四赋值 (1)
P("我说真话"), T
¬P("我说假话"), F
Q(此话是真), T
¬Q(此话是假), F 五结论 (PՈQ)→T
(PՈ¬Q) →F
(¬PՈQ) →F
(¬PՈ¬Q) →F (2)解释之二
罗素悖论(理发师悖论)
According to naive set theory, any definable collection is a set. Let R be the set of all sets that are not members of themselves. If R is not a member of itself, then its definition dictates that it must contain itself, and if it contains itself, then it contradicts its own definition as the set of all sets that are not members of themselves. This contradiction is Russell's paradox. Symbolically:
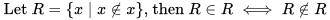
(2)结论
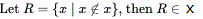 (while R = Q, x = P) (while R = Q, x = P)
(证毕)
| 





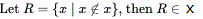 (while
(while 