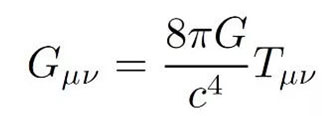| 801川普開金口,必有伏筆;要言引力場方程 廣相論42 |
| 送交者: 和顏清心 2019年08月07日13:49:10 於 [教育學術] 發送悄悄話 |
|
29分
《引力場方程》 親愛的朋友,
今天我們要對引力場方程作個總結:
引力場方程描述了時空的幾何性質。
這是一個張量方程。
引力場方程的性質是屬於‘非線性偏微分方程’。
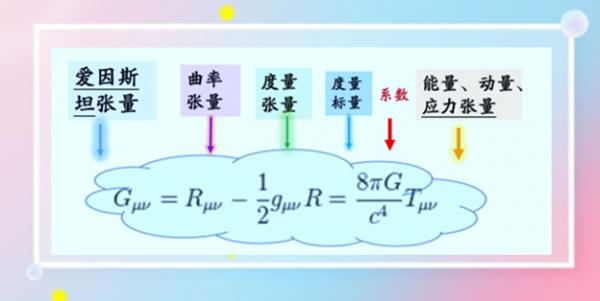
場方程的“張量”,都有2個希臘字母來作下標,
如,Guv (愛因斯坦張量) 等。 這種帶2個字母下標的張量,叫“二階張量”。
μ 近似音讀 繆/mju:/, ‘繆斯’的‘繆’;
ν 近似音讀 妞 /nju/ 。‘妞’當女孩講。
在古代,繆斯是主管藝術和科學的九位女神的總稱。
G,也是Grace (優美)的第1個字母, 我們可以用‘Grace科學女神’來幫助記憶。
如上述,作為引力場符號的G μν ,學名叫
‘愛因斯坦張量’。引力:Gravitation ,頭一個字母,是G。 愛因斯坦張量 G μ ν是個大概念。
大概念下又有 7 個小概念:
第1小概念:
“曲率張量” R (μ ν) :
“曲率張量”用來描述彎曲空間的曲率。
在微分幾何中,它的學名叫“黎曼張量”
或叫“里奇張量”。
【曲率,即,彎曲程度。就是說,
彎曲空間偏離 平直空間 的程度,用曲率表示。】
“黎曼(里奇)張量”是說,
在某種邏輯推演中,
空間曲率的數學描述是可以得到簡化或‘縮並’的。
註:縮並是一種有關簡化的運算。
縮並,可以在某種邏輯推演中,將一種複雜的張量,
經過推演而等價於一種較為簡單的張量。
第2小概念:
“ 里奇標量(R) ”: “ 里奇標量(R) ”代表純量曲率, 它是從“里奇張量”簡化形成的; 所謂標量(即數量)是不涉及方向的量。 “里奇標量 “R”也是一種曲率,
只不過這種空間曲率, 是在特殊條件下的空間曲率。
“ 度量張量 “度量張量 ”,也叫度規張量,
是用來衡量4維空間的距離和角度的。
在引力場方程中,
度量張量與里奇標量 乘積的二分之一 1/2 自然也是一種張量,
這個張量同樣也可看作是 彎曲空間曲率的數學描述。
“能量-動量-應力張量 能量-張量-應力,也稱 ‘能、動張量’,等。
“能-動-應力張量 ”
代表空間的能量密度和動量密度等。
這個張量也是二階的。
第5個小概念: G(Gravitational constant)是“引力常數” ;
第6個小概念: C是真空中的光速。 第7個小概念 π是圓周率,是基本的幾何常數之一。
好了,寫到這兒里,
我們是否可以對場方程有些印象了。 綜上所述,愛因斯坦場方程,
表述的是“空間彎曲”的情況。
數學上的空間彎曲,從何而來?
就是從‘愛因斯坦場方程’推演而來的。
已經得到天文觀測的驗證。
愛因斯坦場方程,是廣義相對論的核心, 它使用數學語言精確地描述了 物質的性質與時空的聯繫。 場方程使用了黎曼幾何中的概念和方法。 在黎曼幾何中, 空間(或時空)的幾何性質 被一個叫做'度規張量' 的概念所描述。 眾所周知,簡單的坐標 不能提供足夠的信息, 來描述球面或更複雜空間的幾何性質。 這些信息,只能由“度量張量”等來描述。 “度量張量”是定義在曲面空間中所有點的函數。 所有與幾何相關的量, 比如曲線的長度、兩條曲線相交的 角度等,都能通過“度量張量”計算出來。 我們知道,時空、物質等都是互相聯繫的。 愛因斯坦通過用一些較小概念(曲率張量等), 來推演另一個較大概念 G μν, 以這種方法來表示這些聯繫。 引力場方程可以簡化成,如下形式:
愛因斯坦場方程的意義 這個方程 一邊是幾何量;一邊是物理量 即, 左邊是描寫時空性質的幾何量; 右邊是描寫物理性質的物理量。 就是說,愛因斯坦引力場方程
是用等號連結了‘空間結構’
和‘空間中物質、能量的分布’,
或者說,彎曲時空
等於空間中的物質、能量的分布 憑這個方程, 可以對時空和物質 是如何相互影響的在數學領域有了了解。
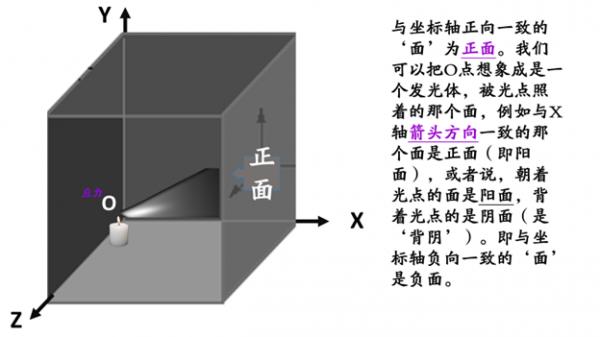
《有關‘應力分量’的正負值問題》 應力分量是能確定物體中
某一點應力狀態的3個相互垂直面上的
正應力和剪應力,共9個應力量。 為了計算應力分量, 首先要確定該應力 所在‘截面的(坐標軸的)方向’, 然後再確定‘應力作用的方向’。 具體的說,是要找出: ‘應力分量’的法向。法向即法線的方向。 習慣上,我們取三個正交截面的應力向量 (即x軸、y軸或z軸), 分別為三個截面各自的法向。 就是說, 為規定應力分量的正負號, 首先假設:法向 與坐標軸正向一致的面為正面; 與坐 標軸負向一致的面為負面。 進而規定: 正面上指向坐標軸正向的應力為正,反之為負; 負面上指向坐標軸負向的應力為正,反之為負。 三個正面上共有九個應力分量 (包括三個正應力和六個切應力)。
在標準空間直角坐標系里, 分別將X軸、Y軸或Z軸箭頭所指方向,稱為正向; 反之則是負向。
model of a perfect communion, help us to receive jesus worthily
完美的聖餐儀式,幫助我們接受耶穌的信仰。謝謝。 |
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2018: | 昨天我發布的打印論文被宰之事。美國白 | |
| 2018: | 《兩片嫩葉》 | |
| 2017: | 關於量子保密通訊 | |
| 2017: | 2018美國留學費用表 | |
| 2016: | 和顏清心:思想的形成 人問寒山路 | |
| 2016: | 思想的形成 不是風動、不是幡動,仁者 | |
| 2015: | 是騾子是馬拉出來遛遛-你真的英語好嗎 | |
| 2015: | 令人噓唏不已的耶魯大學原址 | |
| 2014: | 老幾:胡適對孔子思想的誤解 | |
| 2014: | 範例的微觀世界與宏觀世界的關係 | |