| 也談乘除法算理及其功用 |
| 送交者: 裕雄 2023年06月26日01:25:13 於 [教育學術] 發送悄悄話 |
|
日前所發文章“也談乘法表述及交換律”在朋友中散發傳閱後,得到了積極的反響和支持,也有不同的意見反饋。筆者又做了進一步的了解與思考,製作了乘除法算理的示意圖,加寫了“情境教學可否取代算理”的一段。由於內容的擴充,思考的深入,標題也改了。本文包含前一篇的全部內容,閱讀本篇即可。 也談乘除法算理及其功用 沈乾若 乘法表述是否應該區分被乘數與乘數,是小學數學爭論的一個焦點。2001年頒布的《全日制義務教育數學課程標準》,將傳統的“被乘數×乘數=積” 的表述改為“乘數×乘數=積”。著名留美數學教育專家馬立平博士形容此舉“打掉了支撐着大半壁算理體系的承重牆”。而倡導方則辯稱這座承重牆並無必要,新的乘法表述更符合乘法交換律。 本文對被乘數與乘數的區分和乘除法算理系統作進一步的探討,希望算理更為簡潔,協調一致。並對當下依賴情境教學、取消算理體系的作法提出了質疑。當然,本文的出發點是基礎數學教學,而非數學理論。 一.被乘數與乘數的區分 數學知識源於生產和生活的實際,也在物理等學科之中孕育發展。 在小學引入乘法運算,是從“一行栽樹8棵,3行可以栽多少棵?”、“一盒雞蛋12個,5盒幾個?”這類計算物體個數的實例着手的。這裡,被乘數與乘數的區分清清楚楚。 到小學高年級和中學,乘法的涵義很快深化,應用範圍將大大拓寬。尤其物理學科中,例子比比皆是: 例1. 密度與質量:鐵的密度為7.87克/厘米3,計算一個1250厘米3鐵塊的質量。 算式:7.87g/cm3 ×1250cm3 = 9838g 例2. 勻速運動:一輛汽車每小時行駛75公里,7小時行駛多少公里? 算式:75km/h × 7h = 525km 例3. 熱容量與溫度變化:一壺水的熱容量為5230焦耳/攝氏度,將水從200C燒開,需要提供多少熱量? 算式:5230J/0C × (100-20)0C = 4.184 x 105J 三例中,被乘數分別為密度,速度和熱容量;乘數為體積、時間和溫度變化;而作為乘積的質量、路程和熱量,則是乘法運算的目標和結果。參與運算的,是一個個完整的物理量;不但數字,單位也在其中。乘數的單位通過約分都被約掉,留下的恰好是乘積的單位。單位體現的是一個物理量的量綱,告訴人們它是什麽;甚至比數字更為重要。 從以上三例可見,被乘數與乘數量綱不同,意義不同;更不要提牛頓第二定律F = ma、歐姆定律 V = IR等公式中的質量與加速度,電流與電阻等各種不同的物理量了! 比照以上三例,“一行栽樹8棵,3行栽多少棵?”的算式為“8棵/行×3行=24棵”;“一盒雞蛋12個,5盒幾個?”應寫作:”12個/盒×5盒=60個“。即使最簡單的例子,乘法中的被乘數與乘數各自也具有不同的單位,承載不同的意義。二者的區分乃客觀存在,並非人們所強加。 再者,3個雞蛋加2個雞蛋等於5個雞蛋;然而3個雞蛋不能乘2個雞蛋。每碗3個雞蛋乘兩隻碗是可以的;正如速度可以乘時間,密度可以乘體積,熱容量可以乘溫度變化;等等。相加的通常是同一集合的元素,而相乘的一般屬於不同的集合。故加法不必區分被加數與加數,而被乘數和乘數的區分則有它的道理。 事實上人們爭論比較多的,是相乘的元素在乘法算式中的順序。國內規矩,被乘數在前而乘數在後,寫錯扣分沒商量;儘管交換位置並不影響結果的正確性。這種做法讓人感覺過於刻板,帶來取消被乘數與乘數區分的變革。 英語中,被乘數為Multiplicand, 乘數為Multiplier;區分是顯然的。但算式怎樣寫則未完全統一;有的先寫被乘數,有的先寫乘數,不像國內那般嚴格。寫前寫後畢竟是人訂的規則,有商討的餘地。同時也有的教科書採用“因子x因子=積”的表述,對二者不加區分。 二. 乘法表述的承重牆和三層台階 小學數學中,從計算物體個數的簡單實例入手引入乘法,得到的傳統表述為:“每份數×份數=總數”,它相當於“被乘數×乘數=積”,但意義更為清晰。這一表述提供了對乘法的實質性理解和把握;而且簡單明了,小學生容易懂,也利於牢固掌握。 然而,這一表述是否可以涵蓋意義較為複雜的乘法?譬如,前面的三例乘法是否符合這一表述呢? 首先考查三例中的被乘數:密度為單位體積的質量,速度為單位時間駛過的路程,熱容量為物體溫度每提高一度所吸收的熱量;將它們抽象為“每份數”是恰當的。而作為乘數的1250厘米3、7個小時和80個攝氏度的溫度變化,可以說都是“份數”。故三個乘法算式均契合“每份數×份數=總數”。與剛引入乘法時不同的只是,每份數、份數和總數不限於整數。 其他如“加速度×時間=速度變化”,“壓強×面積=壓力”,“功率×時間=功(或能量轉換)”;等等,均為“每份數×份數=總數”的模式。至於牛頓第二定律, 歐姆定律等公式,儘管表面上不易看出;細究起來,亦暗含該模式,或其延申和變形。這一點此處不贅。 可見,小學數學中,從計算物體個數抽象得來的“每份數×份數=總數”的表述,不但揭示了乘法的實際意義,而且為日後理解科學中更複雜的乘法預留了空間。 數學與科學中新概念的建立,眾所周知,依據的除生產與生活實踐外,還有已確立的概念。乘法即建立在加法的基礎之上。引進乘法之初,很自然地將其解釋為“若干相同加數之和”。其中加數為被乘數,加數的個數為乘數;如前所述,清清楚楚。此為理解乘法的第一個台階。 但這樣的解釋,第一隻適用於乘數為整數的情況,第二未能深入乘法的本質。切實理解乘法,須上升到第二層台階,即“每份數×份數=總數”。這一表述提供了對乘法的實質性理解和把握,提升了思維;是比“相同加數之和”更為到位的解釋。 用此表述,作為乘法的逆運算,除法的算理水到渠成:總數除以份數為等分除,總數除以每份數則為包含除。 將乘法延伸到分數與小數,用此表述亦輕而易舉。譬如6 x 2/3,按照“被乘數×乘數”的順序,解釋成每份6個,2/3份。而2/3×6 的意思是每份為2/3, 共6份;意思也很清楚。若再以6個2/3相加來解釋,好比上了第二層台階又退下去,從第一階賣力跨到第三階,沒有道理。 可見,小學乘除法的教學中,“每份數×份數=總數”的表述發揮着重要作用,“承重牆”的說法不為過。 那麽,什麽是乘法概念的第三層台階呢?乘法的核心,無非一個“倍數”概念,包括分數、小數或百分數作為倍數。乘法即“求某一數量的若干倍”。這個第三層台階,是我們的目標,也是每個懂得基礎數學的人所理解的乘法。 上到了這一層,含分數和小數乘除法的解釋簡便易行,甚至不必拘泥於“每份數x份數=總數”。分數作除數的算理是一個難點,但用倍數概念解釋起來卻頗為簡單。以4 ÷ 2/3為例,可以有兩種解釋。對應於包含除的是,求4為2/3的多少倍?另一種,一個數的2/3是4,求這個數,則對應於等分除。 抽象化、一般化是數學的目標。由“相同加數之和”, 到“每份數×份數=總數”,達到“求某一數量的若干倍”;乘法表述的這三層台階,由簡單到複雜,由具體到抽象,由個別到一般;為學生思維的訓練和素養的提升提供了一段科學的路徑。 三. 乘除法算理的圖示
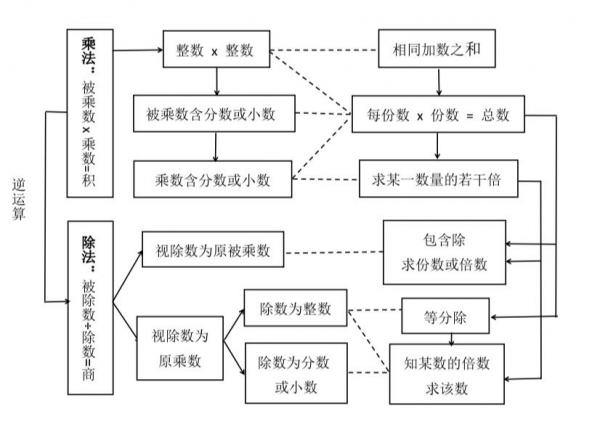
綜合以上論述,乘除法的算理可用上面的示意圖來表示。示意圖左半部分為乘除法的各種運算;右半部分為算理,即運算的意義。虛線表示二者的對應關係。箭頭表示運算及其算理是怎樣層層遞進的;就乘法而言,即前面所說的三層台階。 示意圖清楚地揭示出從整數到分數和小數各類乘除法運算的涵義,及各部分之間的邏輯關係;它們構成一個有機的整體。 兩點說明。第一,筆者並非認為此圖所示為唯一正確的乘除法算理。若能進一步簡化、優化,使之更為和諧一致,當然最好。第二,乘除法算理遵循人們的認識過程,主要是為初學者預備的。算理的講解須融入運算的學習,為理解運算服務。萬不可將算理當作另一套理論灌輸給學生,要求學生死記硬背,從而加重他們的負擔。 四. 關於乘法交換律 取消被乘數與乘數的區分,倡導者的依據是乘法交換律。我們來看一看這樣做是否合理。先定義乘法,才談得上兩個數能否交換。“一行栽樹8棵,3行栽多少棵”與“一行栽樹3棵,8行栽多少棵”儘管結果相同,畢竟先要懂得並算出24棵,才得到答數相同的結論。定義乘法而以交換律為依據?邏輯上不大說得通。 3個8和8個3皆為24,確實很簡單。然而,在初學乘法的小孩子腦中,這樣說不無幾分抽象,需要以實物來支撐。故我們只能從“一行栽樹8棵,3行栽多少棵”這樣的情境着手。 交換律適用於純數字相乘。或者說,交換律只是在做數值計算時可以使用。在實際問題中,交換被乘數與乘數的數字結果相同;但這樣做除極少數情況外,要麽改變了情境,要麽失去了意義。 面積計算似乎是支持交換率的一個較強的例證,屬於前面提到的“極少數情況”。如一張長30cm、寬20cm的紙,面積的計算:30cm×20cm = 600cm2,或 20cm×30cm = 600cm2 均可。但若這樣端給小學生,他們不一頭霧水才怪!學生能夠接受的講法是::1cm2是邊長為1cm的小方塊;把紙分為30行,每行寬1cm;得知每行有20個方塊,乘以30行,從而算出600cm2的面積。故算式為:30cm2/行×20行 = 600cm2。請看,被乘數與乘數的區分繞得開麽? 再者,本文討論的乘法為標量相乘的基本運算。以後的數學或物理課還會學習矢量乘法,甚至矩陣相乘,等等。其中有的交換律成立,如矢量之間的點乘;有的不成立,如叉乘。故即使不考慮單位,交換律於乘法也並非理所當然,需要十分注意。 五.情境教學可否取代算理? 課程標準規定不再區分被乘數和乘數之後,小學數學教材中只剩下“乘數×乘數=積”的表述,及倍數和平均分等若干概念的說明。傳統的算理體系消失殆盡,新的體系卻無蹤影;連“除法為乘法的逆運算”都未提及。 這很自然。“乘數×乘數=積”的表述並未提供有實際意義的信息;很難用來解釋分數或小數乘法;更不用提解釋除法,特別是作為難點的分數除法了。 那麽,我們的教學是如何讓學生懂得乘除法,並且能夠加以運用的? 翻開時下的小學數學課本,筆者不禁暗暗吃驚。目之所及,處處是圖畫,描繪日常生活、動植物、科技知識等各種各樣的場景。實例之豐富、具體、直觀,洋溢着以前的教材所沒有的氣象,更遠非國外的教科書可比。 本世紀以來的新課改強調“創設情境”,這一說法來自美國,來自西方。然而事實上,國外數學教材純數學的成分居多,應用題在數量和種類方面都差得遠;即使小學數學也存在這一問題。“情境創設”仍然不足,“問題解決”更未落實。由於缺少實例的支撐,應用題從來都是難點。不會應用除法,在國外中小學生中非常普遍。 國內則真刀真槍,實實在在下了功夫。教材中成千上萬的實例,其背後的工作量非同小可。國內教育界付出的巨大努力,由此可見一斑。 回到我們的問題:國內學生是怎樣學會乘除法的? 沒有了算理系統,教科書和教師授課通常依據具體情境給出解釋,並確定運算方法。比如從運動類題目得到“速度×時間=路程”的公式;求速度時則用路程除以時間。從購物類題目得到“單價×數量=總價”,那麽總價除以單價則得到數量。又如,由除以2相當於乘以1/2, 推出除數為分數的情況下顛倒相乘的計算方法。至於一個數除以分數的實際意義,則避免做一般性的討論。 正是在眾多實際情境的浸潤之下,學生得以懂得乘除法,基本上掌握了它們的應用。 然而,抽象化、一般化、培養邏輯思維能力乃數學的宗旨;情境教學而不提升到一般性規律,我們是否走向了另一個極端?是否有偏離數學正軌之嫌?儘管每一部分的解釋都有道理;但支離零散,缺少關聯,不成系統的解釋,終歸差強人意;達不到數學的目標與應有的境界。 人認識事物的過程包含一往一返的兩個階段,第一階段從個別到一般,從具體到抽象,得出概念與理論;第二階段從一般到個別,從抽象到具體,驗證和應用理論於實際問題。第一階段的思維方式是歸納、猜想之類;第二階段則主要為演繹思維。演繹推理乃數學中大量訓練的思維模式。 顯然,沒有提升到一般性規律的情境教學,不完整、不到位,也缺少演繹推理的訓練。具體到乘除法,缺了算理,學生可以應付一般的題目,但欠缺解決深層次問題的能力。 數學歸根結底玩的是概念。“需要逐步養成從概念出發思考和解決問題的習慣,概念缺失對後續數學大廈的建立是有較大影響的”,數學教師楊磊如是說。
2023年6月 鳴謝: 本文在寫作過程中筆者與楊磊、韋煒進行了討論,吸收了他們的觀念;特此致謝。 同時感謝張景中院士的指導和啟發。
作者簡介: 沈乾若,北京大學物理系畢業,北京航空航天大學工學碩士,加拿大西蒙菲沙大學數學博士。《加拿大博雅教育學會》名譽會長,《融匯中西教育論壇》召集人。具備中國大陸和加拿大數十年大、中學教學及辦學經驗。現為獨立教育學者,從事比較教育研究。研究方向為教育體制與政策,基礎數學與科學教育。
|
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2022: | 聽師父講故事 (小故事.大道理) 信 | |
| 2022: | 玄學基礎(5) | |
| 2021: | 鮃鰨鰈,三種躺平的有脊椎動物。 | |
| 2021: | 被人怕好還是被人愛好? | |
| 2020: | 好的教育,是公平的 | |
| 2020: | 年僅20歲來自義大利的大提琴手 | |
| 2019: | 783、善有善報、看圖學概念 廣相論26 | |
| 2019: | 唐詩解(修訂19 | |
| 2018: | ★ Site Web élégant FHY Net, où | |
| 2018: | 有錢也不要捐給 Great Fire.org這個造 | |