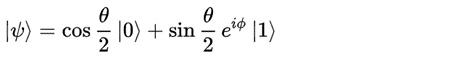| 淺談量子計算機-1 |
| 送交者: 天蓉 2023年11月19日13:30:15 於 [教育學術] 發送悄悄話 |
**** 1. 前言 ****計算機技術的發展有目共睹。回味計算機歷史饒有趣味,1946年誕生的世界第一台電子數字計算機:體重30噸,占地面積170平方米,看起來像一棟大房子。70多年過去了,如今的科學技術,已經將這個龐然大物縮小到裝進我們的口袋裡。 人類的好奇心和探索精神永無止境。科學家尤其如此,他們並不滿足於傳統計算機,總是異想天開,企圖另闢蹊徑,希望解決某些經典計算機無法解決的難題。近幾年來,量子計算機這個新名詞逐漸進入了人們的視野。那麼,什麼是量子計算機呢?它和經典計算技術有何不同?有哪些優越性?進展情況如何? 本文簡單介紹一下量子計算機,包括基礎知識、主要算法,以及物理實現、發展概況等。 **** 2. 歷史 ****
也許你會感到奇怪 計算機的能力已經如此強大,為什麼還要研發量子計算機呢?是科學家們別出心裁多此一舉吧?其實是因為經典計算技術中難以解決的“複雜度”問題。
量子計算的起源要追溯到上世紀70年代,計算機科學的發展啟發了多位科學家,對此有了初步想法並開始發表文章。除了幾位計算機科學家之外,其中物理學家費曼起了重要的作用。費曼正是因為對量子理論的深入理解,才能提出量子計算技術的設想。
那是在1981年 美國MIT的校園裡,召開了物理和計算技術“聯姻”的第一次會議。費曼作了一個報告,揭開了研發量子計算機的新篇章【1】。費曼提出一個問題:經典計算機可以被用來模擬量子世界嗎?答案是否定的 因為在模擬量子現象時,經典計算機的計算量,將隨着系統(粒子數N)的增大而指數增加。費曼認為微觀世界的本質是量子的,N非常大,是傳統計算機在有效時間內解決不了的問題,也就是如前所說的“計算複雜度”問題。
“複雜度”表徵的是所需計算量與問題涉及系統變量數N之間的關係。複雜度分時間和空間,時間複雜度指的是所需計算時間T與系統變量數N之間的關係;空間複雜度指所需比特數B與N之間的關係。兩者實際上互相關聯,我們以時間複雜度為例。
一般來說,計算時間將隨着系統增大而增加。但T的增大因問題而異,T與N可以成線性關係,也可能成平方關係,也有可能是隨着N指數增長。可以用函數 O(1)、O(N)等等來表示複雜度,即表示T隨N增加的快慢。
時間複雜度包括:線性關係O(N)、平方關係O(N2)、立方關係O(N3)等等,最困難的是指數關係:例如O(2N) 【2】。 費曼的設想使得基於量子力學的計算機的研究被提上了科學發展的歷程,物理學家和計算機科學家們都一直在努力。20世紀90年代,量子計算機的幾類重要算法得以發展。2013年後,諸如加拿大的D-Wave等真實的量子計算系統陸續出現。隨着谷歌、英特爾、IBM等大公司的加盟,量子計算機的量子比特數越來越多,谷歌2019年宣稱實現量子霸權,2022年底,IBM發布433量子比特量子計算機,此外,這方面中國也不落後。儘管這些成果中不乏商業炒作,但技術上在不斷進步,量子計算機逐漸走向實用,也是有目共睹的。
**** 3. 基礎 ****
3.1 疊加態
量子計算的方法與經典計算完全不同,兩類計算機速度差異的原因來自於量子現象和經典現象物理規律的不同。量子計算基於量子規律。量子規律的精髓是什麼?其實可以用一句話來概括:種種奇怪的量子現象都是來自於量子“疊加態” 【3】。
你也許聽過最奇怪的量子現象是“糾纏態”和雙縫實驗,不過實際上,糾纏態也是一種疊加態,是多粒子體系狀態疊加產生的效應,而各類“詭異”的雙縫實驗均可用疊加態解釋。
什麼是疊加態呢?根據我們的日常經驗,一個物體在某一時刻總會處於某個固定的狀態。狀態可以用位置、速度、相位、能量等物理參數表示。比如我說,我現在在客廳里,或者說,我現在在房間裡。要麼在客廳要麼在房間,這兩種位置狀態必居其一。然而,在微觀的量子世界中卻有所不同!微觀粒子可以處於一種不確定的狀態中。例如電子可以既在A又在B,電子的狀態是“A”和“B”兩種狀態按一定概率的疊加,這種混合狀態就是疊加態。
微觀量子世界的粒子一般都處於“疊加態”,但是我們卻觀測不到疊加態!因為“觀察測量”的行為將引起所謂“波函數塌縮”或者被詮釋為“退相干效應”,即觀測之前是疊加態,觀測之後疊加態不復存在,“坍縮” 成了一個確定的狀態!因此,我們只能“以某種概率“觀測到疊加的多個本徵態之一。例如,如果盒子中的”薛定諤貓“化身微觀粒子,它的狀態可以被表示成“死貓”與“活貓”的疊加態。然而,只要你打開盒子觀測,疊加態就塌縮了!你有50%的可能性看到“活貓”,50%的可能性看到“死貓”,但你看不到“既死又活”的貓,換言之,你觀測不到它們的疊加態!(圖3.1)。
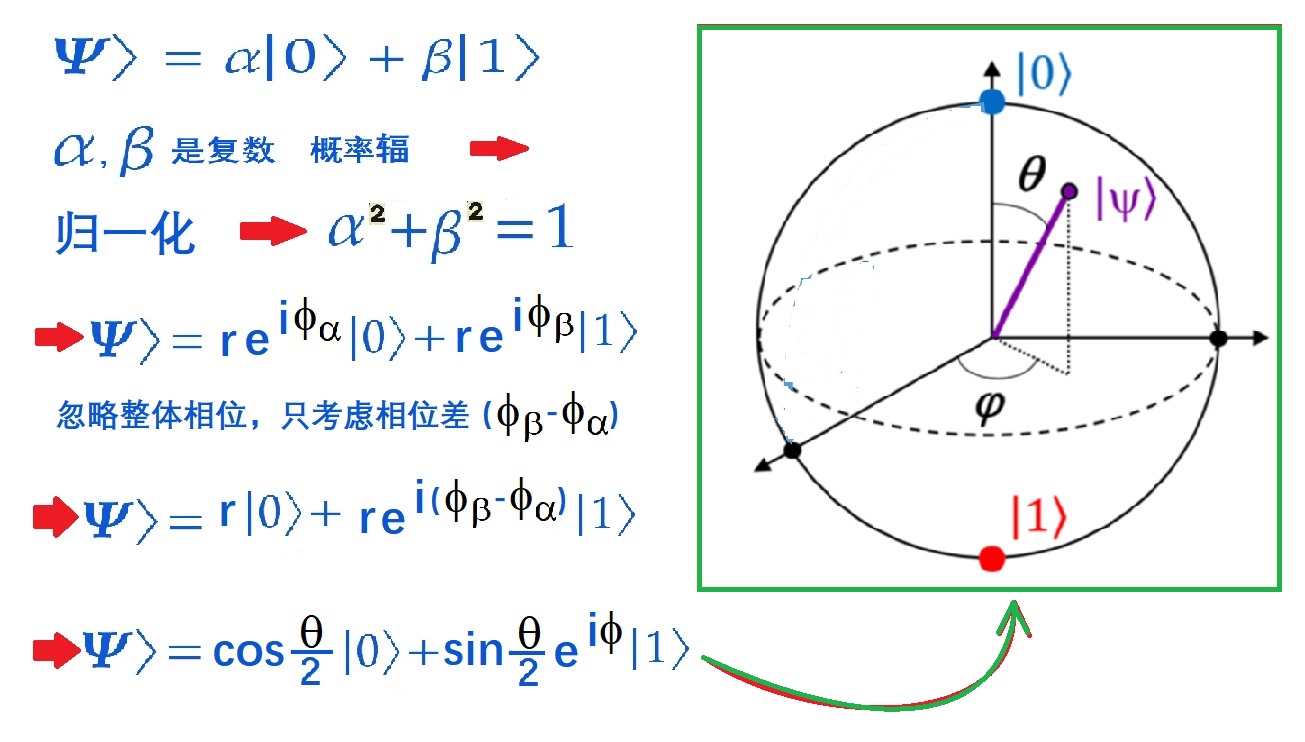
圖3.1:疊加態和塌縮
如圖3.1左上角,是疊加態波函數的公式,也就是:|y> = a|0> + b|1>。
因此,疊加態通常用2分量量子系統來表示,式中的|0>和|1>表示系統的兩個本徵態。
3.2 量子比特
量子計算與經典計算的主要區別是運算單元:經典計算機基本運算單位是比特,量子計算機基本單位是量子比特。量子比特(Qubit)也叫量子位(元),實質上就是疊加態。
疊加態可以用布洛赫球面來直觀描述。什麼意思?如上所述,疊加態|y>可表示為兩個本徵態|0>和|1>的疊加:|y> = C1|0> + C2|1>。這兒的C1,C2是兩個複數,因此,本徵態|0>和|1>,以及疊加態|y>,都可以看作是兩維複數(希爾伯特)空間中的矢量。兩維復空間對應於4維歐氏空間,兩個複數對應4個實數變量。但是,因為這兩個複數C1,C2的平方分別代表疊加態|y>被測量時,塌縮到本徵態|0>和|1>的概率,因此C1,C2滿足歸一化條件,此外,可以忽略沒有物理意義的整體相位,這樣一來,便只剩下兩個參數。被兩個參數描述的所有疊加態,在4維空間中構成一個超曲面。更進一步,該超曲面對應於3維歐氏空間的一個球面,這就是布洛赫球面。
圖3.2:布洛赫球面的來龍去脈
如圖3.2所示,疊加態|y>可以表示為球面上的一個點:
量子比特與比特,兩者物理內容完全不同,具體實現也是天壤之別。比特用電壓的高低兩個值很容易實現,實現量子比特有多種方法,都非常困難。
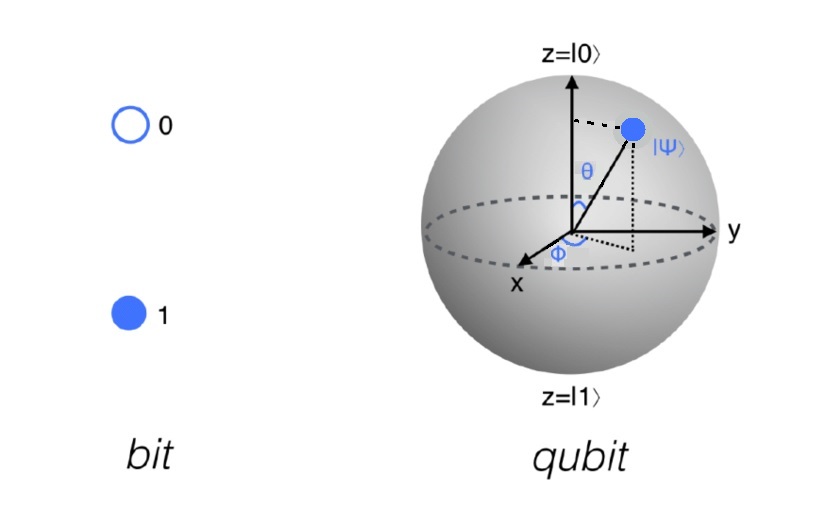
比特只有兩個狀態是0和1,而量子比特的疊加態|y>有無窮多,因為布洛赫球面【4】上的任何點都是一個疊加態。每一個時刻,比特只有(0或1)1個值,而量子比特的疊加態同時有2個值。理解量子比特,是理解量子計算技術的關鍵。
圖3.3:比特和量子比特
疊加態作為量子比特,有兩個關鍵點必須強調。
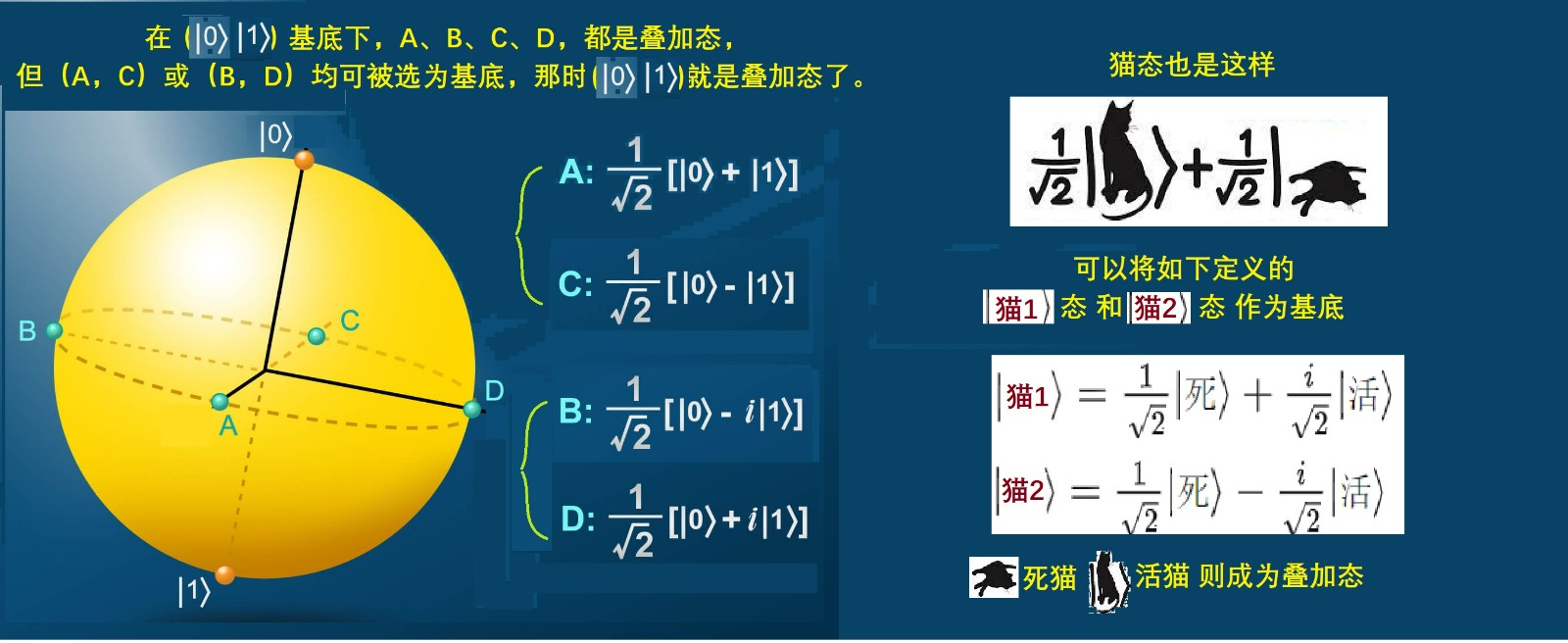
1,量子世界的本質是隨機的,這個意思可以從本徵態疊加態之關係理解。本徵態和疊加態是相對的,依賴於物理量,也取決於(量子比特)基底的選擇。例如對薛定諤的貓,一般我們說 “死貓”與“活貓”是基底,又死又活、半死不活是疊加態。然而這不是絕對的,也可以將又死又活 半死不活當作基底態,而“死貓” “活貓”便成為了疊加態,見圖3.4。因此,原以為是固定態的基態,實質也是疊加態,所以本質上都是疊加態。
圖3.4:疊加態和本徵態是相對的
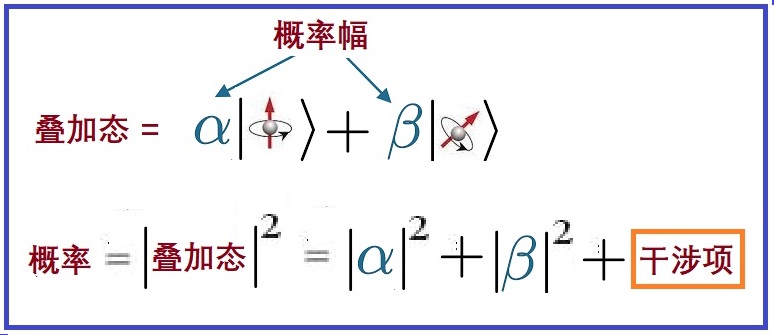
2,疊加態疊加什麼?疊加的是概率幅不是概率。概率幅和概率是不一樣的,它們的區別很重要。如果兩個本徵態互不正交,概率幅疊加會產生干涉項,見圖3.5。概率幅疊加後,模的平方中,除了兩個基態係數模之外,還有兩個基態的相干項,包含了兩個波函數相對相位的信息,即兩個波函數是相干的。
而經典的概率疊加,僅是概率混合的統計現象。量子物理中概率幅的疊加,反映了波動的本質。量子疊加能產生干涉,多種狀態同時存在,使得量子計算機能同時對多種狀態進行計算,即可以對特定算法進行平行計算,這是量子計算快於經典計算的奧秘所在!
圖3.5:概率幅疊加產生干涉項
機器的“計算”是什麼意思呢?經典計算中有許多邏輯門:例如AND(與門),OR(或門),以及NOT(非門)與非門或非門等等。這些邏輯門的各種組合,將各個“比特”的0、1狀態變來變去,便能夠完成各種複雜的計算。量子比特也需要類似概念:“量子門”!量子門作用在Qubit的疊加態上,將Qubit變成另一個狀態。
可以用2維矩陣代數的語言來描述疊加態(Qubit)的變化。量子比特是布洛赫球面上一個矢量,Qubit狀態的演化,就是布洛赫球面上矢量的旋轉。旋轉是由用幺正(酉)矩陣表示的“量子門”引起的。矩陣(量子門)作用在矢量上,將Qubit的狀態變成新的狀態。許多Qubit、許多量子門連在一起,量子計算便如此一步一步進行下去。所有Qubit的最後狀態,便是計算得到的最後結果。 (待續) Contents **** 1. 前言 **** **** 2. 歷史 **** **** 3. 基礎 **** 3.1 疊加態 3.2 量子比特 3.3 量子門 3.4 量子電路 **** 4. 算法 **** 4.1 Grover 量子搜索算法 4.2 多伊奇算法 4.3 秀爾算法-1(經典,數論部分) 4.4 秀爾算法-2(量子部分) **** 5. 實現 **** ********************************************************** 作者部分YouTube視頻: https://www.youtube.com/watch?v=0I8FdazqAvc&list=PL6YHSDB0mjBKB2LBZDKL9UhcMMx6GtOsx https://www.youtube.com/watch?v=_d0wquZkOYU&list=PL6YHSDB0mjBJ6qgfin-xKmP3FtTQr4x7i ********************************************************* |
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2022: | 悄悄告訴你獲得千萬福報的秘訣? | |
| 2022: | 現代化中國人心的話語——心語架構式話 | |
| 2021: | 情理兩線思維--良善開發於本心 | |
| 2020: | 關於內蒙消減蒙語教學內容的信 | |
| 2019: | 紅歌擇菜(九)花兒為誰紅 | |
| 2019: | 《五燈會元》禪宗公案解 | |
| 2018: | 習【雜阿含經】第1經 (第1卷) | |