| 淺談量子計算機-3 |
| 送交者: 天蓉 2023年12月09日16:46:31 於 [教育學術] 發送悄悄話 |
**** 4. 算法 ****
4.1 Grover 量子搜索算法
為什麼需要量子算法?因為經典算法不足以體現量子計算特別之處。量子算法的目的便是要利用量子比特量子門的特殊性:疊加性、干涉性、糾纏性……,構造比經典計算快得多的算法。此外,量子算法也需考慮物理可實現性。
圖4.1:量子算法發展史
在考慮量子算法時,特別需要關注量子計算的如下特點: 1,量子比特是量子疊加態,幾個本徵態按不同的概率幅疊加起來; 2,量子計算可以平行計算(或者說對疊加態進行某種“操作”),但是不能測量。因為一旦測量就將導致系統的“波函數塌縮”,即疊加態以一定的概率塌縮到某個本徵態,塌縮概率是該本徵態概率幅的平方。
Grover量子搜索算法【6】展示量子計算機解決“非結構化搜索問題”的速度可以比經典更快。
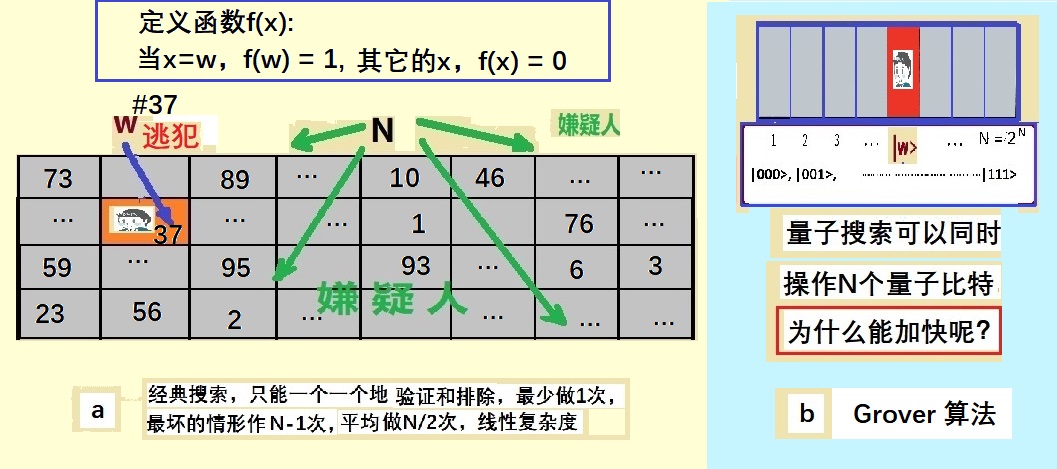
給你一個很大的N個項目列表,其中有一項w是我們希望找到的。或者用一個最簡單的比喻,假設我們是要在許多嫌疑人中搜索一個逃犯,w表示的就是逃犯。
考慮最簡單的情況:N個嫌疑人x中只有一個罪犯w,如圖4.2a所示。首先將列表中的每個候選者標以特定顏色,逃犯w為紅色,所有其他人x都標以灰色。規定某種方法判定逃犯,例如考慮一個與“計算”有關的方法:假設我們知道罪犯的身份證號碼w,可將它與所有嫌疑人的號碼x比較,即做減法計算(x-w)。結果則可以用一個二元目標檢驗函數f(x)表示:如果x不等於w,f(x)=0;如果x是逃犯,即x= w,f(x)=1。因為嫌疑人的數據x是無序的,如果使用經典方法,要找到逃犯的號碼w,只能一個一個地做減法。最壞情況需檢查所有N個嫌疑人,最好情況也得檢查1個,平均而言必須做N/2次減法。因此,經典搜索的運算次數與N的關係是線性的:O(N)。
現在考慮量子搜索,假設“數據庫”由量子比特可能處於的所有計算基組成。例如 3 個量子比特,如圖4.2b所示,計算基列表就是:|000>, |001>,……|111>,即從0 到7八個值,量子搜索可以同時操作這8個寄存器。但是,一開始我們並不知道要找的逃犯w在哪裡,所有的嫌疑人都有可能是罪犯。因此,似乎我們也只能一個一個地計算驗證!如果那樣的話,仍然需要和經典情況一樣的線性複雜度N,體現不了量子運算的優越性。
圖4.2:搜索問題和檢驗函數f(x)
既然均等概率體現不了量子計算的特點,就想辦法讓概率變化。Grover算法就是非常巧妙地利用了量子計算機可以“平行運算”的特點,同時對N個寄存器反覆進行某種操作,使得目標項w的概率幅|w>不斷放大,其他的概率幅|x>不斷縮小,這種算法可以只用sqrt(N) 個步驟找到罪犯w。比較經典計算需要的N步,得到了平方級的加速。
聽起來增速不多,僅僅平方級的加速。但實際上是我們所能期望的搜索算法最大加速。 並且當N很大時,二次加速確實可以節省大量時間。比如有100個嫌疑人,身份證號碼1到100,隨機無序地分布在100個寄存器中,找出數字37的所在之處,經典方法需要平均做50次操作,量子方法只需要做10次!N越大,加速越明顯。此外,該算法的用途不止於數據搜索,具有通用性,可以為各種其他算法獲得二次運行的時間改進。
Grover 算法的核心就是振幅放大技巧,將目標w的概率幅放大,而將其它“非目標項”x的概率幅縮小。振幅放大過程分兩步:量子黑箱函數Uw(也稱Quantum Oracle),和擴散算符操作Us(Diffusion Operator)。
圖4.3:振幅放大的幾何解釋
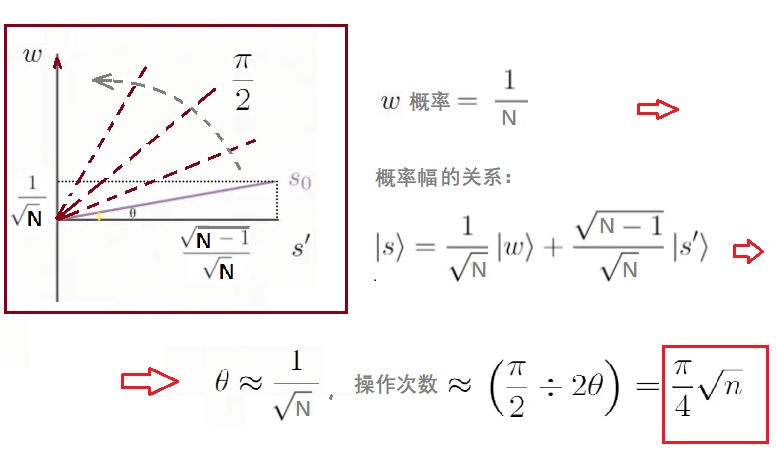
“振幅放大”算法有很好的幾何解釋,表示為態矢量在一個二維平面中產生旋轉,如圖4.3所示。初始狀態是一個均勻疊加態|s> ,|w>和|s>張成向量空間中的一個二維平面,兩個向量|w>和|s>並不完全垂直,因為|w>也以N1/2的概率輻出現在疊加態|s>中。然而,我們可以引入一個額外的狀態|s‘>,它位於|w>和|s>構成的二維平面上但垂直於|w> 。
更詳細地分幾步說明:剛才的初始態算是步驟 1 ,振幅放大過程從均勻疊加|s>開始,均勻疊加態|s>可以很容易地從n個H門作用於n個量子比特基態|0>上構造出來,得到如圖4.3左圖所示的初始狀態。在|w>和|s‘>構成的平面坐標下,初始狀態|s>可以表示為:
|s> = sinT |w> + cosT |s‘>,
角T = arcsin(s在w的投影) = arcsin(1/ N1/2),圖4.3左下圖形是均勻疊加態|s>的bar圖。
步驟 2,應用黑箱函數Uw將狀態|s>翻轉,見圖4.3的中圖:Uw的作用是將目標狀態|w>反相,其它狀態不變。從幾何上講,這對應於|s>態關於|s‘>軸的翻轉。這意味着狀態|s>中|w>的幅度變為負值,也意味着平均幅度(由虛線表示)的降低。
步驟3,現在關於狀態|s>應用另一個擴散算符Us。此轉換將|s>映射到狀態UsUw|s>。兩次反射Us和Uw對應一個旋轉,將初始狀態|s>旋轉得更接近|w>,見圖4.3右圖。
幅度條形圖中Us的反射操作可以理解為關於平均幅度(虛線)的反射。由於第一次反射降低了平均振幅,這變換將|w>的振幅提高到其原值的數倍,同時也降低了其他振幅,故稱為振幅放大。
然後我們轉到前面重複步驟 2和步驟3,繼續振幅放大的過程直到達到要求。
圖4.3所示的過程的確可將振幅放大,但到此為止我們有兩個問題:一是圖中的黑箱函數Uw和擴散算符Us具體是什麼?二是此過程要重複幾次才能找到w呢?
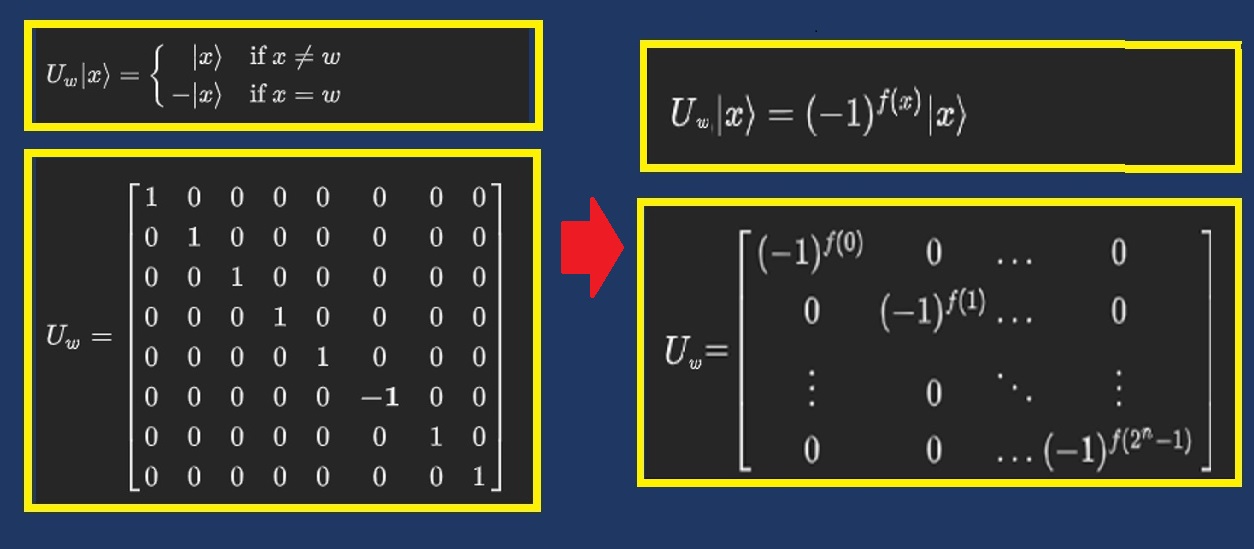
Grover 算法的預言機Oracle函數Uw所做的,是給解|w>添加了一個負相位,也就是說,對於計算基中的任何狀態|x>,可以創建一個函數 Uw:Uw (x) = x,如果|x>不等於|w>;而Uw (x) = -x,如果|x>等於|w>,如圖4.4a所示。該函數被稱為Oracle。
圖4.4:a)黑箱函數將w反相;b)相位黑箱函數
圖17a中,黑箱函數Uw可以表達為一個對角矩陣,其中對應於目標項w的值為-1,其它為1。圖4.4a下圖表示三個量子位 的Uw矩陣。進一步具體而言,Oracle可以用圖4.2b中所示的經典檢驗函數f(x)構成的相位函數來實現。
也許有人會說,既然Uw可以將w那一項反相,不是已經知道了w的位置嗎?那還搜索什麼呢?這是初學Grover算法時經常感覺困惑的問題。這兒需要再次強調量子計算的特點:可以讓多個寄存器同時運算但不能檢查每個寄存器的結果。因此,雖然我們說Uw能夠將w反號,但因為沒有進行測量,我們並不知道是哪個寄存器的結果反相了。反相的結果是每個寄存器根據它自己內部的數據檢驗f(x)而反饋回來的。
換句話說,每個嫌疑人自己知道他是不是罪犯,但我們並不知道,除非進行測量!
即使進行測量,僅僅是將|w>反號這一個操作,也不能確定w的位置。因為|w>是概率輻,而測量得到的是概率,即概率輻的平方。|w>符號的改變使概率輻反相,但並不會影響概率。Grover算法的巧妙之處是在步驟3中我們又應用了一個擴散函數Us = 2 |s>
那麼,現在回到第二個問題:此過程U要重複多少次才能使w的概率幅達到最大值呢?
每一步過程U,都使態矢量的位置更接近|w>的位置,假設每次改變的角度是均勻的2 q,對初始態|s>作用t次之後:|yt> = (UwUf)t|s>。最後需要的次數可用圖4.6的描述來粗略地理解。
圖4.5:Grover算法
事實也證明旋轉N^1/2次就足夠了。 能從經典的N次減到N^1/2次,原因是由於處理的是概率輻而不是概率,即被放大的是概率幅而不僅是概率,這也是量子計算秘訣所在。
圖4.6所示的是用IBM量子模擬的2量子比特搜索過程。經典需要3次比較,量子Grover算法只需要1次。
圖4.6:搜索算法舉例
參考文獻: 【1】Keynote talk, 1st conference on Physics and Computation, MIT, 1981。(International Journal of Theoretical Physics, 21: 467–488, 1982) 【2】Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein; 殷建平等譯. 第1章 算法在計算機中的作用. 算法導論 原書第3版. 北京: 機械工業出版社. 2013年1月 【3】張天蓉. 世紀幽靈-走近量子糾纏(第二版)[M].合肥:中國科技大學出版社,2020年5月。 【4】Bloch Sphere(wikipedia),https://en.wikipedia.org/wiki/Bloch_sphere 【5】IBM Quantum (2022). estimator primitive (Version x.y.z) [computer software]. https://quantum-computing.ibm.com/ 【6】Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212 相關視頻: (待續) Contents **** 1. 前言 **** **** 2. 歷史 **** **** 3. 基礎 **** 3.1 疊加態 3.2 量子比特 3.3 量子門 3.4 量子電路 **** 4. 算法 **** 4.1 Grover 量子搜索算法 4.2 多伊奇算法 4.3 秀爾算法-1(經典,數論部分) 4.4 秀爾算法-2(量子部分) **** 5. 實現 **** ********************************************************** 作者部分YouTube視頻: https://www.youtube.com/watch?v=0I8FdazqAvc&list=PL6YHSDB0mjBKB2LBZDKL9UhcMMx6GtOsx https://www.youtube.com/watch?v=_d0wquZkOYU&list=PL6YHSDB0mjBJ6qgfin-xKmP3FtTQr4x7i ********************************************************* |
|
|
 | ||
|
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2022: | 關於中華團結聯合協會 | |
| 2022: | 淨空老法師:淨土大經科註(第四回)24 | |
| 2021: | 索達吉堪布:金剛經釋 4 | |
| 2020: | 利他利己都歸仁 | |
| 2020: | 100萬億倍? | |
| 2019: | 我在美國家中的書房 | |
| 2019: | 490誰將是中國的華盛頓;用世之學,莫 | |
| 2018: | 用國內法律追緝外國犯罪嫌疑人是國際慣 | |
| 2018: | 《評胡亥的博客“張首晟“師承無德” | |