| AI教父辛頓:從反向傳播到凡人計算 |
| 送交者: 天蓉 2024年06月11日13:20:39 於 [教育學術] 發送悄悄話 |
|
傑佛瑞·埃佛勒斯·辛頓(Geoffrey Everest Hinton,1947-)【1】,被譽為“AI教父”,他一生的理想是要明白“人的大腦是如何工作的”?機器是否能模仿大腦的運作機制?為此他花了半個世紀的時間開發神經網絡,他在1986年和2022年,分別發表了兩篇與神經網絡算法相關的重要論文,一前一後相隔三十多年,一反一正都是討論機器如何學習的問題。哪一種算法更接近人腦的運作模式呢?辛頓對此有與眾不同的觀點,此文將為你解讀這兩篇文章的核心思想,然後,你對上述問題便能得出你自己的答案了。
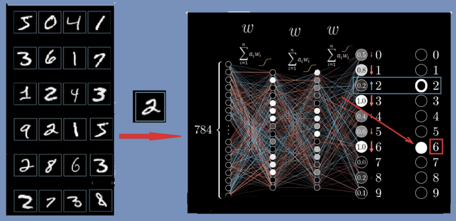
圖1:辛頓的兩篇論文 反向傳播算法 1986年,辛頓與David Rumelhart和Ronald Williams共同發表了一篇題為“通過反向傳播誤差來學習”(Learning representations by back-propagating errors)的論文【2】。 三位科學家並不是第一個提出這種“反向傳播”方法的人。但他們將反向傳播算法應用於多層神經網絡並且證明了這種方法對機器學習行之有效。他們的論文也證明了,神經網絡中的多個隱藏層可以學習任何函數,從而解決了閔斯基等書中提出的單層感知機存在的問題。 “反向傳播”是“誤差反向傳播”的簡稱,是人工神經網絡的一種自我學習算法。說到學習,我們自然地聯想到人類大腦的學習過程,例如孩子學習識別“貓和狗“那樣,是從反覆的經驗和錯誤中學習。機器學習也是這樣,我們在計算機中,首先構造一個由輸入層、輸出層,以及多個隱藏層組成的多層神經網絡,這就像給計算機建造了一個”人工大腦“。然後,我們需要訓練這個大腦,讓它學習使其具有”智能“。學習和訓練有各種方法,“深度學習”是其中一種,這個方法由“梯度下降”和“反向傳播”反覆迭代而完成。下面以“識別手寫數字“的例子來簡要說明這個過程,圖2。 手寫數字的每個樣本,比如圖2中所示的“2”,被掃描後用28*28=784個實數替代,送到神經網絡的輸入節點上。這個神經網絡,除了784個輸入節點外,還有10個輸出點,表示從0到9的數字。輸入和輸出中間有兩個隱藏層(每層16個節點),第一個隱藏層分辨數字圖像中的一些小片段,第2層則分辨“圈”“線”一類的筆畫結構,然後,根據樣本圖像所具有的結構,輸出層得出判斷:是0到9中的哪一個。 類似於人體的神經系統,不同神經元之間有不同的關聯,人工網絡中節點與節點之間的關聯用一系列權重參數wi來表示。也可以說,權重參數wi代表了節點激活下層節點的概率。參數wi的數目很多,即使是圖2中這個簡單4層網絡的例子,所有的wi參數加起來也有1萬3千多個,訓練的目的,就是要調節好這些權重參數。此外,每個層之間還有一個激活函數,一般可以是不連續的階躍函數,或者常用的平滑可微的sigmoid函數(圖2神經網絡上方所畫曲線)。
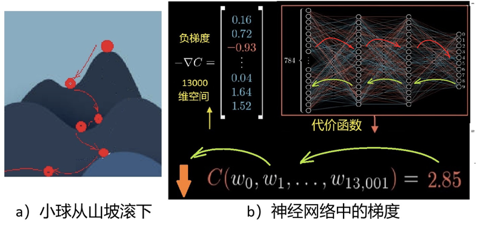
圖2:識別數字的例子 一開始的w參數,是隨機選取的,因此,神經網絡的判斷會出錯。例如在圖2中,輸入的是2,它卻認成了“6”,那怎麼辦呢?就像小孩犯了錯誤一樣,我們需要反覆教他。機器則需要使用大量的數據來訓練它,這就開始了“機器學習”的過程。 如何讓機器學習呢?首先要知道錯誤的來源,那就是來源於這13000個權重參數(可能還包括其它如偏差、激活函數的參數等),因為,最後結果就是用它們代入一個求和公式再乘以激活函數逐步進行運算而得到的。所以,為了調整這些參數,我們根據神經網絡從輸入計算輸出的方法,定義一個誤差函數C(wi)(或稱代價函數、目標函數),如圖3b下方所示C(wi) 的表達式。這樣,訓練的過程就是反覆調整wi,使誤差C(wi)達到我們能接受的最小值。 這些參數wi對誤差函數C(wi)的影響,或稱敏感度,是不一樣的,所以每一次對每個參數調整的幅度也不一樣。敏感度,用數學術語表達,就是梯度。在2維情況下,梯度可以形象地被理解為通常意義下山坡的坡度。坡度有方向,一般指的是一個向上的矢量,向下就叫負梯度,見圖3。
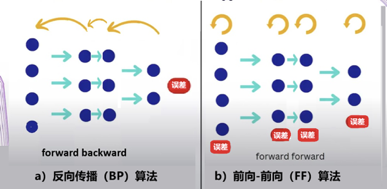
圖3:梯度下降和反向傳播 深度學習中的梯度,原則上與山坡坡度類似,不同的是它是在非常大(上萬上億)的維度空間中的“矢量”。二維情況的梯度可以很容易地畫圖(圖3a)理解,但圖3b中13000維空間的矢量就無法直觀想象了,不過數學上仍然可以定義“梯度”的概念。 要使誤差函數C(wi)達到最小值,類似於我們想從山頂到達谷底。如何找到最優路徑,在最短的時間內到達呢?直覺告訴我們應該朝最陡峭的方向下降,就是說任何時候都選擇最陡的(最大坡度)的反方嚮往下走。這就是機器學習中說的梯度下降算法。不過事實上,梯度下降是一種標準的優化算法,並不是僅僅用在機器學習中。 13000維空間中的梯度計算起來很複雜,而所謂“反向傳播”就是用來計算這個複雜的“梯度”的。在數學上,就是利用微積分中的鏈式法則,來計算偏導數繼而計算梯度。 輸出結果(誤差)被視為是正向計算(如圖3b中的紅箭頭線指向)。要計算敏感度,即每個參數對誤差的貢獻,則可以逐層反向計算回去,如圖3b的綠箭頭線所指。這個過程就是誤差反向傳播,有點像在某項工作中出現了事故後,一層一層反回去秋後算賬追究責任的過程。 藉助於反向傳播,所有的參數得以調整,然後,又根據調整後的參數正向計算出結果,即誤差。如此過程反覆循環直到誤差函數C(wi)接近0,或降到一個我們滿意的數值為止。 當然不能只用一個樣本,比如例子中原來那個“2”,如果那樣訓練出來的機器只能識別那一個“2”。我們需要使用成千上萬的不同數字的樣本來訓練這個神經網絡,最後才能讓它正常工作。 以上學習方法中,反覆的“正向”和“反向”,計算來回進行在輸入端輸出端之間,故也稱其為“端到端”的方法,“Back Propagating”也簡稱為BP算法。 反向傳播的問題 反向傳播算法(BP)是人工智能歷史上一個重要的里程碑,這一算法的提出使得多層神經網絡的學習問題得到了有效解決,為非線性分類和學習提供了可能。基於這種算法,多層人工神經網絡的機器學習逐漸形成了固定的模式,人工神經網絡的研究才重新煥發生機,AI的發展也進入了興盛期。 使用BP的深度學習,逐漸應用擴展於自然語言處理、語音識別、圖像識別等領域,解決了許多實際問題,使得人工智能在各個領域取得了顯著進展。反向傳播法是深度學習當年取得成功的關鍵,至今仍然是這個領域的重要基礎之一,它不斷推動着人工智能的進步。 數學上,BP算法中誤差的反向傳播過程,採用的是已經非常成熟的鏈式法測,其推導過程嚴謹且科學,使神經網絡具有很強的自主學習能力,擁有較強的非線性映射能力,這是它的根本以及其優勢所在。此外,BP算法也具有較強的泛化和通用能力,可以利用從原來知識中學到的知識,解決碰到的新問題。 然而,隨着研究的深入,也逐漸顯現出BP算法的某些缺陷,這使得神經網絡的發展面臨一定的挑戰。反向傳播算法存在幾個問題:一是計算出來的梯度是否真的是學習的正確方向。這在直觀上有些可疑。此外,從數學角度看,BP算法是一種速度較快的梯度下降算法,但由於BP神經網絡中的參數非常多,當網絡包含數百萬或數十億個參數時,也導致有時候收斂速度過慢。並且,梯度下降法容易陷入局部最小值,這時從表面上看,誤差符合要求,但所得到的解並不一定是問題的真正解,所以BP算法是不完備的。 因為BP算法依賴於前向傳遞中計算的可微性,如果某個環節存在不可微的情況,則反向傳播便無法進行。例如,如果我們在網絡中插入一個黑匣子,除非我們知道黑匣子的可微模型,否則將不可能執行反向傳播。 作為反向傳播這一深度學習核心技術的提出者之一,辛頓很早就意識到反向傳播並不是自然界生物大腦中存在的機制。雖然反向傳播非常有用,但它與我們對大腦的了解有很大不同。 近幾年,辛頓在不同場合的演講中都提到這個問題,他的要點是將這種方法與人腦的機制比較: “作為皮層如何學習的模型,反向傳播仍然令人難以置信,儘管人們付出了相當大的努力來發明可以由真實神經元實現的方法”,“沒有令人信服的證據表明皮質明確傳播錯誤導數或存儲神經活動以用於隨後的反向傳播。” 反向傳播中,學習和推理過程是分離的。訓練時,算法必須經常停止推理,以執行反向傳播來調整權重參數,這有別於人腦。我們的大腦源源不斷地接收到信息流,並且實時不斷地進行推理,似乎不像有停下來進行反向傳播的過程。 儘管目前BP算法正在業內用得熱火朝天,但有遠見卓識的大師總是未雨綢繆,考慮的是AI的未來,因此,辛頓根據他的最新研究,在2022年發表了一篇論文【3】,主要有兩個主題。 一是介紹了一種新的人工神經網絡學習算法“forward-forward algorithm”,簡稱為FF算法。二是提出了一種新的“凡人計算”模型。下面兩節分別作簡要介紹。 前向-前向算法 前向-前向算法是一種貪婪的多層學習程序,不同於BP算法的“端到端”(圖4左),它是將學習過程一層一層地完成(圖4右),在每一個單層內反覆計算直接更新參數。也可以理解為,FF是用兩個前向傳播,代替BP的前向+後向傳播,兩個前向計算定格在不同的數據和相反的目標上,以完全相同的方式彼此操作。BP算法中的“代價函數”,在FF算法中,被代之以另一個術語:”好感度“(goodness)。換言之,“正計算”對真實數據進行操作,並調整權重以增加每個隱藏層的好感度,“反計算”則調整"負數據"權重,以減少每個隱藏層的好感度。此外,如果前向和反向通道可以在時間上分開,反向傳遞可離線進行,這將允許數據通過網絡正常運行,而不需要暫停傳播。
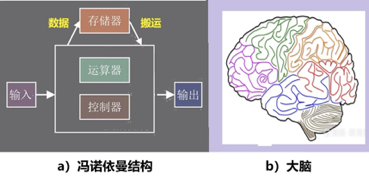
圖4:BP算法和FF算法 與反向傳播不同,FF 算法在包含黑盒模塊時也有效。由於該算法不需要可微函數,因此它可以在不知道模型中每一層的內部工作原理的情況下,仍然可能調整其模型的可訓練參數。 辛頓在由四個全連接層組成的神經網絡上測試了FF算法,每個層包含2,000個神經元。從他的實驗結果,辛頓認為,FF算法仍處於早期實驗階段,比較BP算法,它在速度上要慢一些,但也基本上可以相媲美,其優勢在於可以在前向計算的精確細節未知時使用它,例如使用黑盒模型。辛頓也說,在他用FF算法研究的幾個玩具問題上,通用性不是很好,所以FF也許不會完全取代反向傳播的應用,但FF有兩個意義,首先,它是更為接近大腦皮層的學習模型,其二,它在功率成為問題的應用中有意義。 辛頓的FF算法是他從人腦運作中汲取靈感而提出的。雖然人工神經網絡企圖仿照人類大腦的功能,但許多方面有很大的差別。例如在耗能方面,人腦約有860億個神經元,形成複雜的神經環路和網絡,但其能耗只有20瓦。而大小類似的人工神經網絡的能耗約為8百萬瓦【4】,是大腦的40萬倍。這個差別的根本原因是由於現代計算機的構型所決定的。 辛頓在提出FF算法的論文中,也挑戰了既定的計算範式,提出了一個新的方向:凡人計算。 凡人計算 聽起來這是一個奇怪的名字,是從英文“Mortal computation”翻譯而來,這是什麼意思呢? 在計算領域,傳統上強調硬件和軟件的分離。這種分離有許多優越性,它允許在不深入研究硬件的情況下研究程序,它還允許在數百萬台計算機上使用同一個軟件。但是,這種分離是有代價的,也完全不同於人腦的工作方式。 人類大腦顯然沒有什麼硬件軟件之分,人的智慧和知識,與他的“大腦”實體密切相連不可分,一個人死去了,他的智力也就消亡了,不可能“copy”給另一個人使用。也就是說,人不能“永生”,人類的智力也不能“永生”,而人工智能中的“計算程序”,卻是“永生”的,不會因為某台機器的毀壞而消亡。可以比喻說,目前的“計算”,是個不會死亡的“超人”,而辛頓提出“凡人計算”概念的意思,就是要挑戰此類超人,讓計算,也就是程序,模擬真正的“凡人”。 為什麼要計算成為不能“永生”的凡人呢?因為“永生”需要付出極大的代價,上一節所舉的機器能耗與人腦能耗的巨大差異(8百萬瓦:20瓦)就是其中之一。 從硬件角度看,現有AI系統是基於通用的CPU和GPU,它們都是根據馮諾依曼結構的集中式內存設計的,見圖5。存儲器與其它部分有一定距離。因此,計算過程中數據的搬運造成延遲、耗費能量;而人腦中的基本計算單元都是存算一體的,相當於數據和計算都是分布式的,每個基本單元,既完成計算也存儲信息。
圖5:計算機結構有別於大腦結構 馮諾依曼的通用數字計算機,被設計為忠實地遵循指令,即編寫一個程序,以極其詳細的方式準確地指定機器要做些什麼。辛頓在其新論文中,提出改變這種“計算程序永生”範式的設想。 辛頓寫道:“如果……我們願意放棄永生,那麼執行計算所需的能量和製造執行計算的硬件的成本應該可以大大節省。我們可以允許旨在執行相同任務的不同硬件實例的連接性和非線性發生較大且未知的變化,並依靠學習過程來發現有效利用每個特定實例的未知屬性的參數值的硬件。” 辛頓的想法意味着軟件要逐漸地構建在每個硬件上,並且只對那個硬件有用!即軟件變成了與硬件一起消亡的“凡人”!辛頓認為,儘管這種“凡人計算”存在缺點,但具有明顯的優勢。特別是,如果你想讓你的萬億參數的神經網絡能耗降到幾瓦特的話,“凡人計算”恐怕是唯一的選擇。 辛頓也談到尋找可以在這樣的精確硬件中高效運行的學習程序的問題:或許FF算法就是一個有前途的候選者,儘管它對大型神經網絡的擴展能力還有待觀察。 總之,辛頓這一突破性的想法有可能徹底改變神經網絡的功能,影響人機交互過程,甚至刷新我們對意識的理解。 參考文獻: 【1】Home Page of Geoffrey Hinton,https://www.cs.toronto.edu/~hinton/ 【2】David E. Rumelhart, Geoffrey E. Hinton und Ronald J. Williams. Learning representations by back-propagating errors., Nature (London) 323, S. 533-536,http://www.cs.utoronto.ca/~hinton/absps/naturebp.pdf 【3】The Forward-Forward Algorithm: Some Preliminary Investigations G Hinton,https://bdtechtalks.com/2022/12/19/forward-forward-algorithm-geoffrey-hinton/ 【4】https://news.cnstock.com/industry,rdjj-202403-5207288.htm (本文首發於微信公眾號“知識分子”) |
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2023: | 安徽銀行爆雷!取不出來錢!和平遊行示 | |
| 2023: | 不好笑嗎?用“三起三落 白斬雞”作為 | |
| 2022: | “民主與人民”的基本價值巳被中共徹底 | |
| 2022: | 人類情愛史---原始的激情(歐風亂拂下的 | |
| 2021: | 呵呵,海龜真是莫名其妙啊。你們在美國 | |
| 2021: | 科學研究的藝術 第五章想象力 受條件 | |
| 2020: | 發墳暴典挺總理 自古宰相出地攤 | |