| 從九九表到兩位數相乘 “中國式” 完勝“印度式” |
| 送交者: 北美老表 2016年01月20日06:41:23 於 [教育學術] 發送悄悄話 |
|
從九九表到兩位數相乘 “中國式” 完勝“印度式” 2016年1月3日,在《文學城》上看到了 hhhh的博文,介紹印度小學生心算 20 以內的兩位數相乘方法 ( http:///myblog/10060/201601/501588.html ),我覺得挺好的,轉而就介紹給了幾個微信群的群友。群友們也都覺得很好,有的群友馬上就讓自己家的孩子學做了。也有的群友說不知其所以然,我當天在微信群里做了一下的推演說明: 兩位數“ab” 和兩位數“cd”相乘(a, b, c, d 都是 0 至 9 的個位數字): ab x cd = (10a + b) x (10c + d) = 100ac + 10ad + 10bc + bd = 10(10ac + ad + bc) + bd = 10[(10a + b)c + ad] + bd = 10[(ab)c + ad] + bd 當 a = 1 和 c = 1 時: ab x cd = 10(ab + d) + bd 這也就是 hhhh 介紹的“印度式” 兩位數相乘算法,但只有 19 和 19 以下的兩位數相乘,“印度式” 心算法才成立。 當 a, c 大於 1 時,“印度式” 心算法就不成立了,這就要用到下面介紹的“中國式”心算方法。 用“中國式”心算方法計算任意兩個兩位數相乘,其實並不難,小學生稍加練習,都可以做得到。從上面的推演結果來看: ab x cd = 10[(ab)c + ad] + bd 只要按以下4步,就可以心算出來:
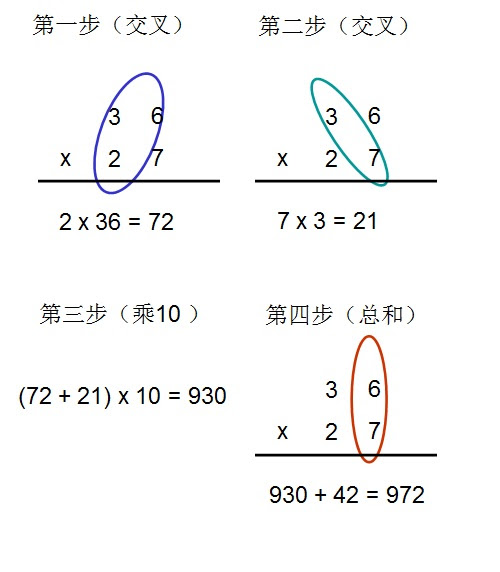
今天,我又非常高興的看到了《文學城》上 hushidai 發表的博文:改進和擴展 “印度式”的心算乘法 ( http:///myblog/68316/201601/522629.html ),與我的推演不謀而合。我覺得這種心算方法,很值得推廣。家長和老師不一定要強求每個孩子都學心算,但是只要孩子們願意學一點心算,掌握任意兩個兩位數的乘法並不難。如果大多數的華人學生都能熟練掌握這一心算方法,那麼,“中國式” 的100以內兩位數相乘心算法,就能輕輕鬆鬆地壓倒“印度式”的20 以內兩位數相乘心算法,呵呵……。 為了方便網友們了解“印度式”和“中國式”心算法,我把 hhhh 和 hushidai 兩人介紹的心算方法轉抄於此處,希望兩位老師不會在意 (如有異議,請與我聯繫,定當更正。謝謝!)。 1)hhhh 介紹的“印度式”心算法( http:///myblog/10060/201601/501588.html ): 印度的九九表是從1背到19(→19×19乘法),不過您知道印度人是怎麼心算11到19的數字的乘法嗎? 看了下面內容之後才恍然大悟,實在太神奇了! 請試着用心算算出下面的答案: 13 × 12 = ? 印度人是這樣算的: 第一步: 先把“13”跟乘數的個位數“2”加起來, 13+2=15 第二步: 然後把第一步的答案乘以10(→也就是說後面加個0) 第三步: 再把被乘數的個位數“3”乘以乘數的個位數“2” 2×3=6 第四步: (13+2)×10+6=156 就這樣,用心算就可以很快地算出11×11到19×19的乘法啦 2)hushidai 介紹的心算法 ( http:///myblog/68316/201601/522629.html ): “交叉互乘” 的心算法具體表述如下: 例 a) 36 X 27 = ? 36 是被乘數; 27是乘數 第一步(交叉): 2 x 36 = 72; 先把乘數的十位數“2”跟“36”交叉相乘 第二步(交叉): 7 x 3 = 21; 再把乘數的個位數“7”跟“3”交叉相乘 第三步(乘10): (72 + 21) x 10 = 930; 然後把上面兩步的結果先相加,再乘10 第四步(總和): 930 + (7 x 6) = 972; 最後把被乘數和乘數倆個位數相乘後,加上第三步的結果
例 b) 67 X 32 = ? 第一步(交叉): 3 x 67 = 201 第二步(交叉): 2 x 6 = 12 第三步(乘10): (201 + 12) x 10 = 2130 第四步(總和): 2130 + (2 x 7) = 2144
例 c) 16 X 17 = ? 第一步(交叉): 1 x 16 = 16 第二步(交叉): 7 x 1 = 7 第三步(乘10): (16 + 7) x 10 = 230 第四步(總和): 230 + (7 x 6) = 272 *例 c)兼容印度式”20以內乘法。 感興趣的家長,盡可試一試。記性好的華裔兒童,只要稍加訓練,上述四步可全部心算完成,並很快地算出11×11到99×99的任意兩個二位數乘法啦。 謝謝各位華人老師、學生和家長為學習和推廣“印度式”和“中國式”二位數相乘心算法所做努力! 特別感謝: hhhh 介紹“印度式”心算法(http:///myblog/10060/201601/501588.html) hushidai 介紹“中國式”心算法(http:///myblog/68316/201601/522629.html)
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2015: | 請教一個問題。 多謝!! | |
| 2015: | 2013年諾貝爾物理獎介紹 | |
| 2014: | GEORGES,ET AL 著 :中國詩詞曲賦發展與 | |
| 2014: | GEORGES,FAN,et al 著:中國古體詩詞曲 | |
| 2013: | 僑老爺左右腦雙重毒瘤會診 | |
| 2012: | 談談沙石壁崖的“狗熊雙棒體”(I) | |
| 2012: | 未來幾十年的科學發展趨勢 | |
| 2011: | 讚一個!胡總真NB! | |
| 2011: | 肖傳國前傳 | |