當人們學習或思考狹義相對論時,常為它的表述與自己的常識和邏輯上的矛盾而抓狂:當A高速離開B時,B認為自己是靜止的,高速的A的時間變慢;反過來,A也可認為自己是靜止的,B高速離開自己而B的時間變慢。到底誰變慢,似乎永遠說不清。
雙生子佯繆更令人沮喪:假如AB為一對雙生子,A離開B高速到外星旅行,B留在地球上而靜止。當多年後A回到地球時,根據狹義相對論,A因為高速旅行,相會時A比B要年輕。許多人自然會這樣質疑:從B的觀點看,B靜止,A運動,A的時間變慢而比自己年輕;但A也可以認為自己的飛船是靜止的,B的地球在運動,這樣B的時間變慢,結果B比A年輕。看來每方敘述都似乎有理,因而討論陷入一個似乎無法解決的孛倫之中。
到低誰的觀點對呢?答案是A比B年輕。
本文將時空圖的工具,來給出一個解釋。
如果讀者有耐心看下來,也許可以弄清這困擾許多人的問題。你只需高中的數學知識。
以下是時空圖的畫法,為了簡化起見,空間只用了一維。
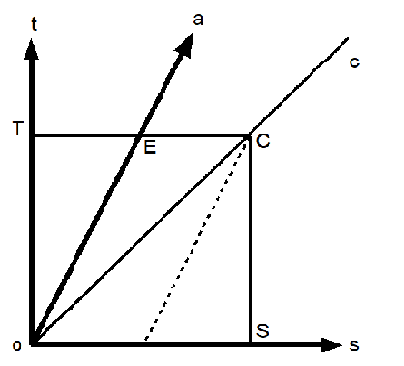
圖中的直角坐標里,ot代表時間軸,os代表空間軸,
oc表示光的運動時空線,如果我們使用一年為一時間刻度,一光年為一空間刻度,當一年與一光年的刻度長度相同時,oc與os或ot夾角都為45度。
如果T為一年的刻度而S為一光年的刻度,三角形oTC是個等腰三角形,或oT=TC。
oT/TC=1表示光速等於一,這是代表光速c的必要條件。
任何與os平行的線被稱為同時線,比如TC,線上任何一點代表空間不同位置上的時間都是相同的。
任何與ot平行的線則稱為等距線,比如SC,線上任何一點代表不同時間裡空間位置到原點的距離是一樣的。
現有一物體從原點出發,oa代表其運動的時空線,隨着時間的流逝,它距原地越來越遠。
如果考慮為運動物體建一新體系,該體系相對原靜止體系運動,我們可畫出它的相應時空圖。對應的座標是平行四邊形。
oa是其時間軸。
對於牛頓的絕對時空觀,os是其空間軸,沒變。
這裡要提到光速不變原理:真空中的光速對任何觀察者來說都是相同的,不管觀察者是靜止或運動。1887年,邁克爾遜和莫雷在美國克利夫蘭做的用邁克爾遜干涉儀測量兩垂直光的光速差值,證明了光速在不同慣性系和不同方向上都是相同的。
以上牛頓絕對時空觀的時空圖會有一重大問題,光速在這裡是EC/OE(E 和 T時間刻度相同,因E在TC的同時線上),因距離刻度EC明顯小於TC而造成光速小於一,光速不變原理在這個時空圖中不成立!
為了滿足光速不變原理,這時空圖必須修改,類似等腰三角形oT=TC的要求,新的運動體系座標的距離刻度應等於時間刻度。我們用oE的等長在光的運動時空線畫出一個交點F,滿足oE=EF。從原點出發的空間軸ox與EF平行,這時它不再與os重合了。(下圖)
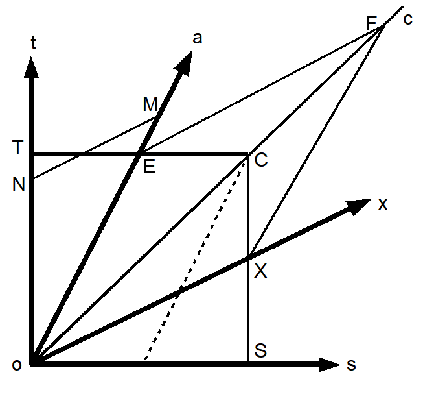
這是個革命性的變革!EF/oE=1,光速等於一,新的時空關係圖滿足了光速不變原理。
任何與ox平行的線為運動體系的同時線,比如EF和NM。它們不再與靜止坐標的同時線平行。同時性的相對性,或不同體系的觀察者對同時的觀念將會分歧,在此顯現出來。
而與oa平行的任何平行線為等距線,比如XF。
假定一年的刻度在靜止體系座標是T點,一年的刻度在運動體系座標是M點。由於靜止體系觀測到運動體系的時鐘會變慢,所以它的一年同時線TC在oa軸上的交點E必須小於一年刻度,或oE對應的時間長度小於oT對應的時間長度。
基於相對性的對等原理,反過來,運動體系觀測到靜止體系的時鐘也會變慢,所以它的一年同時線NM在ot軸上的交點N的必須小於一年刻度T。
為滿足以上要求,M必須在E的上方而N必須在T的下方,NM與TE相交。
由此也看出,運動體系的一年的刻度在幾何上比靜止體系的要長,當運動體系越接近光速,其刻度越長。
空間軸的情況與以上討論類似:運動體系的一光年等距線與靜止體系的一光年等距線相交,每方看對方的長度都會變短。運動體系的一光年的刻度在幾何上比靜止體系的要長,當運動體系越接近光速,其刻度越長。
對於文中第一個問題,如果使用以上討論的相對論時空圖,事情就變得很清楚了:A用了自己的同時線判斷B的時間變慢;B用了自己的同時線判斷A的時間變慢,兩者互不矛盾。
在解釋AB雙生子佯繆時,比較常見和權威的答案是:如果A離開B高速旅行再回來,A會比B年輕,因為B始終在慣性系統中;而A至少經過加速和減速,歷過非慣性系統,所以時間會減緩。該答案是正確的,但人們往往覺得缺少過程和細節的描述,道理完全沒有講得很清楚。
使用以上討論的相對論時空圖來解釋AB雙生子佯繆,會相當清楚和簡單。
下圖表達AB雙生子離別和相會的時空圖。
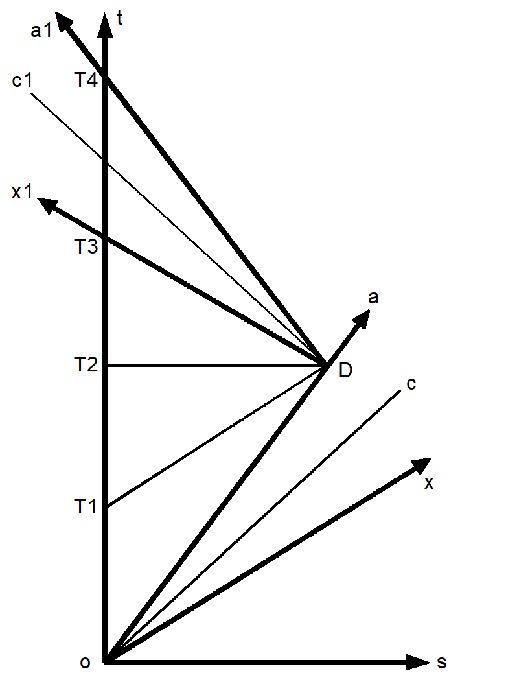
如果A高速離開B,在多年後接近目的地D處,B用靜止體系的同時線T2D認定在T2時刻時,A因高速運動,時間流逝慢了,A較為年輕。
反過來,高速的A在D處用自己體系的同時線T1D認定B的時間在T1處,B比自己年輕。
當A經過減速後真正到達目的地D而與B相對靜止,這時兩者又將共用B的靜止體系--雙方都用T2D的同時線。
如果A具有瞬時超距觀察的本領(因信息傳播受光速限制,這觀察只能是想象的),他在減速時會觀察到,當自己的同時線由高速時的T1D變到靜止時的T2D的過程中,B的時間飛速流逝,從T1跳到到T2,B迅速變老。
從時間刻度比較,基於狹義相對論的時間關係,運動體系oD的時間刻度小於靜止體系oT2的時間刻度,A的時間流逝比B慢。而A對B的觀察中,儘管o到T1的時間刻度比oD小,但加上A減速中T1跳到到T2部分,B的時間流逝還是oT2,比oD大。兩種描述相容,都是oT2與oD相比。
在A從D處回程的旅行中,B在靜止體系判斷A因高速運動,時間變慢,T2T4的時間刻度大於DT4的時間刻度。
這時光的運動時空線為Dc1,A的時間軸為Da1。在A從D處開始高速運動時,Dx1為其空間軸兼同時線。
如用想象的超距觀察,當A從D處由靜止加速到高速時會發現,其同時線由靜止時的T2D掃到高速運動時的T3D(Dx1)的過程中,B的時間飛速流逝,從T2跳到很久將來的T3(因信息傳播受光速限制,這種“觀察到將來”的現象是只可想象而不可能真正實現的)。儘管回程中A也認定B的時間流逝T3T4比自己DT4慢,但B早在A加速時衰老了很多。B的總時間流逝仍是T2T4而比A的回程DT4的時間刻度大,與B的觀察相容。
綜合去來路程,當A回到T4點和B相會時,A一定會比B年輕。









