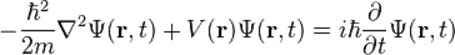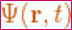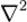| 563、欣賞科學巔峰之光—薛定諤方程二 |
| 送交者: 和顏清心 2018年11月25日22:04:23 於 [教育學術] 發送悄悄話 |
|
《欣賞科學巔峰之光》
親愛的朋友,前面曾經說過, 如果薛定諤方程是高中或大學課程, 我們的文章,就要從小學初級階段說起, 您只要稍稍讀一遍, 就會對這個世界頂級難題, 留下些或深或淺的印象的。
讓我們先從薛定諤方程所依據的‘對應原理’說起。 量子力學可以在原有的經典物理中, 找到與自己相對應的規律。 所謂的對應原理是指在量子數很大的情況下, 量子理論所得結果, 應趨近以往經典物理學的結果,反之亦然。
薛定諤方程所對應的原理, 正是經典物理中的“能量守恆定律”。
讓我們先看一下有關“能量守恆”的例子:
【圖片說明】關於“勢能”減小;“動能”增加的圖示
在這個過程中,“勢能”轉化為“動能”。 看上圖:這個處在下坡道的“騎車人”, 當他處在最高點時, 他具有一個由高度(h) 和質量(m)決定的勢能; 當“騎車人”下坡時, 隨着高度(h)的降低(即高度h值減少), 勢能也在減小;但“能量守恆”, 是不允許能量由“有”而漸變為“無”的, 所以,在勢能減少中, 另一種量,就產生並增加了, 這就是“動能”。
“動能”是由質量(m) 和速度(v)決定的。
在高點時,速度為0,動能也為0, 而隨着“騎車人”高度的降低,速度就變大了, 這就意味着動能在不斷地增大。 這種增加的動能,等於減少的勢能, 所以,使得能量能保持守恆。
“騎車人”到達坡底時, 其勢能抵達最小, 動能則達到最大。
如果此人有“膽”,或者他能像動畫片那樣, 在一瞬間將自己連同車子,全都化為一個圓球, 如同下面的彩圖所示,
動能和勢能
那麼,這個“人和車”的組合, 就能上衝到與原來的高坡等高的點, 這種上沖之力, 就是一個與下坡相反的力, 但無論怎樣, 其動能(K)與勢能(V) 二者之和的總能(E)是不變的,
即,
總能E = 動能K+勢能V
這個能量關係式, 同樣適用於描述‘微觀粒子’的運動, 只不過微觀粒子的勢能 不是由引力場引起的, 而是由微觀粒子的勢場引起的。
法國王子德布羅意(1892-1987) 沿着能量守恆的思路來想, 經過推演,得出了 ‘動量’與‘波長’關係式(波長 λ= h / 動量p);
薛定諤(1887-1961)在德布羅意的基礎上 利用數學技巧經過繁複地步驟, 推出了微觀粒子的‘波動方程’ (世稱‘薛定諤波動方程’)。 “薛定諤方程(含時的) 是描述物理系統隨時間演化的方程。 在三維空間裡, 彌散於某處的微觀粒子, 其“計算方程(含時的)” 可以具體地表現為:
薛定諤方程中的符號及其含義,如下: m 是質量;
是‘位置 r和時間 t’的波函數; � 是某種計算符號,它代表的是有關‘微分’的計算。 “ψ” ,近似音,讀作“普賽”, ‘普賽’代表波函數 。
“h”是普朗克常數; “E”是所測粒子系統的總能量; “ V”是勢能。 “I”是虛數 虛數可以指不實的數字或並非表明具體數量的數字。
虛數的定義:平方是負數或根號內是負數的數。
注意: 公式中內含的‘總能’ 及其所包含的‘動能’和‘勢能’, 均表達了能量守恆的意義。 未完待續。謝謝閱讀。
|
|
|
 | |
|
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2017: | 322 鈎沉古天文學的萌芽和發展 | |
| 2017: | 兒子的一句話讓我眼窩發熱 | |
| 2016: | 從解放人民到鎮壓人民–中共四十年來的 | |
| 2016: | 平凡又神秘的詩人 | |
| 2015: | 地球人類的語言與天上的語言是矛盾的 | |
| 2015: | 簡單解釋一下青藏高原歌詞 | |
| 2014: | 小樵 :哈佛家長周末 | |
| 2014: | 再談對“分析哲學”的批評 | |
| 2013: | 華人家長多學信息及知識讓生活,工作更 | |
| 2013: | 家長何需打着燈籠為孩找苦吃? | |