| 592、從最簡單的學起——洛倫茲變換式 |
| 送交者: 和顏清心 2019年01月18日03:16:22 於 [教育學術] 發送悄悄話 |
|
《狹義相對論》 第4章 伽利略變換式和洛倫茲變換式 一、伽利略變換式
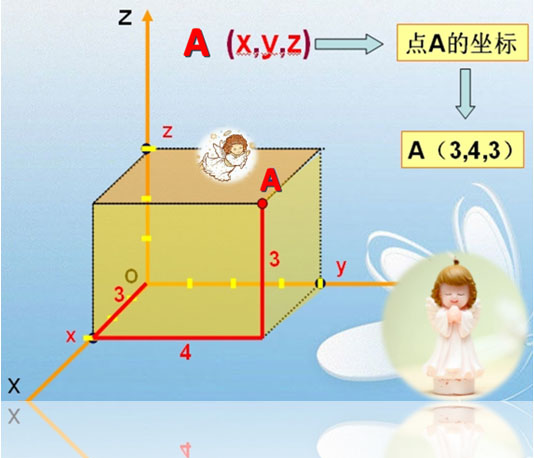
就會對‘伽利略變換式’產生誤解。 所以學習前, 需要複習一下有關“坐標”和“坐標系”的基礎知識。 如果對“坐標系”沒有一個清楚地了解, 在以後的學習中,就會產生嚴重的誤解。 現在,看到不只在一本書上, 甚至在某些流行文章中, 都不能避免地有原則錯誤。 所以,真的需要細緻些理解那些 與“變換式”有關的知識。 也許是認為“坐標”概念太簡單了, 幾乎查遍了網上的資料, 竟然沒有找到一個令人信服的定義, 這使後學者在‘胡嚕吞棗’的學習中,越學越亂。 為了使學習建立在踏實的基礎上, 不得不從頭說起。 1、什麼是“坐標”? 簡言之, “坐標”是按某種方法所選取的“一組數據”, 這組數據叫“坐標”。 詳細些說, “坐標”是為了確定平面或空間中某一點的位置, 而在平面或空間中取一個點作為“原點”, 過此“原點”,再作2條或3條兩兩垂直的“軸線” (數軸),在“軸線”所形成的2維平面 或3維空間中的任何一點, 都可以用“坐標數據”來表示。 例如,下圖“點A”的坐標,即為(3,4,3)。
2、什麼是“坐標系(統)”?
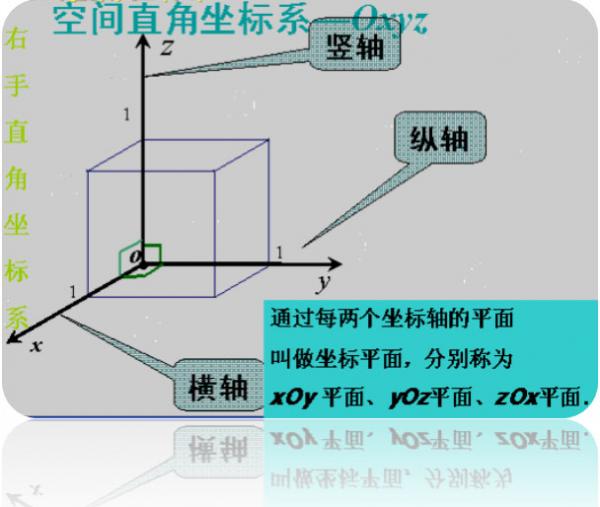
“坐標系(系統)”是由“原點”、 “數軸”、“面”或“空間”(卦限) 及“坐標數據”這4 或5 種要素組成的。 為了說明“點”的位置、運動的快慢、方向等 (為了確定平面或空間某點的狀況), 必須選取相應的‘坐標系’。 或者說,為了定量地描述物體的位置及變化等, 需要在參考系中建立相應的‘坐標系’。 坐標系的種類很多,常用的坐標系有“直角坐標系”。 此外,還有“柱面坐標系”“球面坐標系”等, 這些複雜的坐標系,不是我們在這兒要學習的內容。
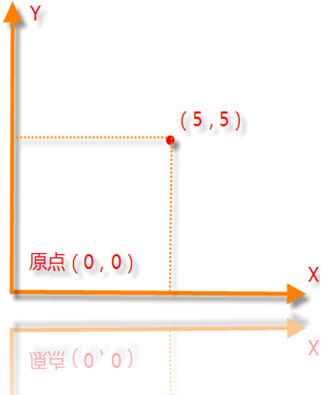
註: 坐標軸的箭頭象徵着, 其所指的方向可以無限延伸。 所謂“橫、豎”與“縱、橫”, 本來分別是2對“反義詞”, 這裡卻把4個詞用在一起。 那麼,為什麼會有“橫軸”“豎軸” 和“縱軸”的稱呼呢? 即,為什麼“x軸”叫“橫軸”、 “y軸”叫“縱軸”?這或許是從二維“直角坐標系”發展來的。所謂二維“直角坐標系”,參見下圖,
如圖示,二維的直角坐標系, 是由2個互相垂直的軸設定的, 通常分別稱為“x橫軸”和“y縱軸”; 兩個坐標軸的相交點,稱為原點,標記為O。 三維坐標系,在原本的二維直角坐標繫上, 再添加一個垂直於x軸和y軸的坐標軸, 稱為z軸(“豎軸”)。 在三維空間的任何一點P, 可以用“直角坐標” (x、y、z) 來表示。
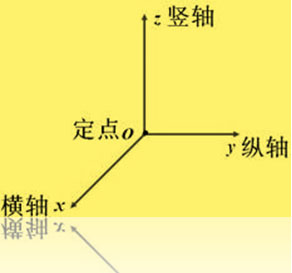
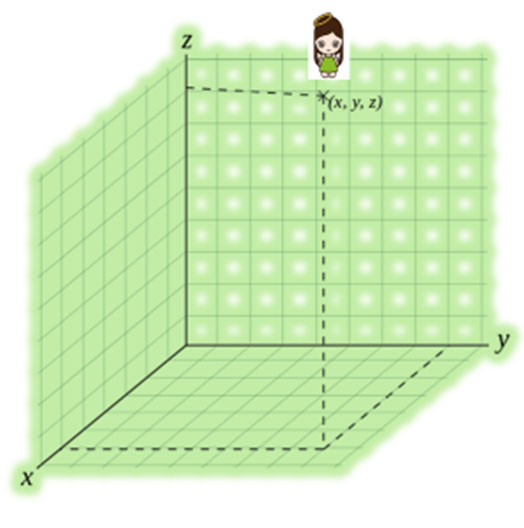
例如,下圖,某點的直角坐標是(x,y,z ) � �
�三維直角坐標系: �
�x軸的方向是親近讀者的; y軸的方向是遠離讀者的。 坐標軸的箭頭象徵著, 往所指的方向無限延伸。 在三維空間的任何一點P, 可以用‘直角坐標’ 來表示其位置。 例如,參閱上圖,某點
� 謝謝閱讀
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2018: | 打死卞校長案的處理,人心難平 | |
| 2018: | 362 世界上唯有兩件東西能深深地震撼我 | |
| 2017: | 航億葦:中國的博士99%都是假的! | |
| 2017: | 【亂象剖析】教師為何不再傳道? | |
| 2016: | 重大刑案,公安要尋情報組織援助 | |
| 2016: | 121.無分別心 | |
| 2015: | hare:維度(範例解釋) | |
| 2015: | D.QU著:"反格長相思令"詞譜之首創及其 | |
| 2014: | 事實與原則(1)-事實的定義 | |
| 2014: | 李揚:疆獨理論無歷史依據 | |