德國數學家帶了三個博士生,用了6個月,完成了雞蛋的畫法:把兩個釘子定在要畫的紙面上,用一根線,一頭綁在左邊的釘子上,一頭綁在畫筆上,畫筆繞過右邊的釘子以後,拉直線落筆,就是半邊雞蛋的軌跡。然後再畫另外一邊。注意,筆的左邊是單線,筆的右端是雙線。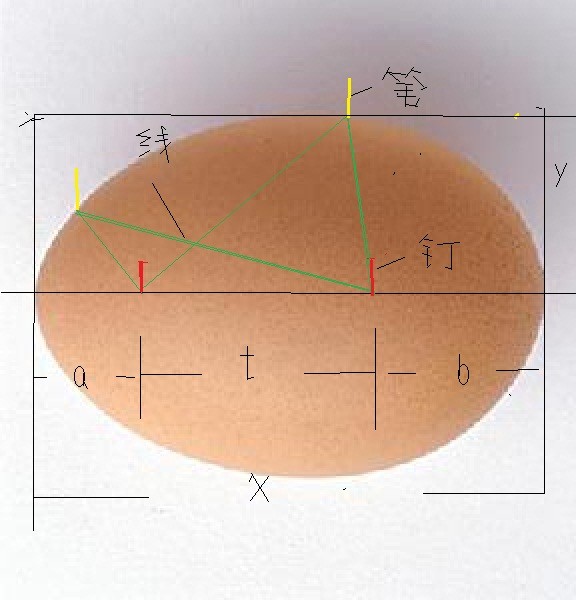
設:
雞蛋長度為x,
寬度為2y,
線長度為w,
兩個釘子距離為t,
雞蛋小頭頂端到左邊釘子距離我a,
雞蛋大頭頂端到右邊釘子距離為b。
雞蛋的大小形態與這6個數值有關。
x=a+b+t;
w=2t+3a=t+3b;
b=t+a/3;
a=b-t/3。
t 給定以後,a與b成正比,w與a和b成正比,w與y和x成為正比。
w給定以後,t與b成反比,t與x成為反比,t與a和b成反比。
問題還有很多,例如,
雞蛋的表面積怎麼計算?
雞蛋的體積怎麼計算?
最基本的是雞蛋剖面(矢狀面)面積怎麼計算?
雞蛋隨意放的時候重心在哪裡?
---------------------------------------------------------------------
雞蛋研究新“壯舉”:雞蛋形狀新通用方程誕生
科學家發現一種通用數學公式,可描述自然界中存在的任何鳥蛋。
英國肯特大學的研究人員與合作實現了一個長久以來未獲成功的壯舉:他們發現了一個通用的數學公式,可以描述自然界中存在的任何鳥蛋。相關研究近日發表於《紐約科學院年鑑》。
雞蛋形狀一直吸引着數學家、工程師和生物學家的注意。雞蛋是如何進化出現在的形狀的?這個謎題一直受到科學家高度重視。
雞蛋足夠大,可以孵化出一個胚胎;又足夠小,可以以最有效的方式離開動物體內;不會蛋一下出來就滾走,它的結構足夠牢固可以承受重量,並成為許多物種生命的開端。因此,雞蛋被一些科學家稱為“完美形狀”。
對所有鳥蛋形狀的分析採用的都是四種幾何圖形:球形、橢球形、卵形和梨形。目前,梨形的數學公式尚未導出。
為了糾正這一點,研究人員在卵形公式中引入了一個額外的函數,開發了一個數學模型來擬合一個完全新穎的幾何形狀,其特徵是球形-橢球形演化的最後階段,它適用於任何鳥卵幾何學。
這個雞蛋形狀的新通用數學公式基於四個參數:雞蛋長度、最大寬度、垂直軸的移動,和1/4蛋長直徑。
作者表示,這個長期尋求的通用公式不僅是了解雞蛋形狀本身的重要一步,而且是了解它是如何和為什麼進化的,從而使廣泛的生物和技術應用成為可能。
目前,關於雞蛋形狀的所有基本數學描述已在食品研究、機械工程、農業、生物科學、建築和航空學中得到應用。作為實例,該公式可應用於蛋形薄壁容器的工程構造,蛋形容器的強度應高於典型的球形容器。
作者在文中指出,這個新公式是一個重要的突破,潛藏着多種應用。包括對生物物體的科學描述。由於現在可用數學公式來描述雞蛋形狀,因此生物系統學、工藝參數優化、蛋的孵化和家禽的選擇等方面的工作將大大簡化。
“同時,可以對生物體物理特性進行準確而簡單的測定。對於研究孵化、加工、儲存和分類雞蛋技術的研究人員和工程師來說,雞蛋的外部特性至關重要。”作者指出,有必要使用雞蛋體積、表面積、曲率半徑和其他指標來描述雞蛋的輪廓,而新公式提供了一個簡單的識別過程。
此外,它還可以用於未來與生物學相關的工程。雞蛋是設計工程系統和尖端技術的天然生物研究系統。雞蛋形狀的幾何圖形被採用在建築中,如倫敦市政廳的屋頂,因為它可以以最小的材料消耗,承受最大的負荷,這一公式可被輕鬆應用。
“正如這個公式所證明的那樣,生物進化過程如卵子的形成,必須通過研究進行數學描述,它可以作為進化生物學研究的基礎。”肯特大學遺傳學教授、新研究通訊作者Darren Griffin說,“這一通用公式可以應用於基礎學科,特別是食品和家禽行業,並將推動對雞蛋的進一步研究。”
“這個數學方程強調了我們對數學和生物學之間某種哲學和諧的理解和欣賞,並從這兩種方式進一步理解宇宙,巧妙地理解了雞蛋的形狀。”肯特大學訪問研究員、文章共同通訊作者Michael Romanov說。論文第一作者、該校前訪問研究員Valeriy Narushin也表示:“我們期待看到這個公式在從藝術到科技、從建築到農業的各個行業的應用。這一突破揭示了為什麼來自不同學科的合作研究是至關重要的。”






