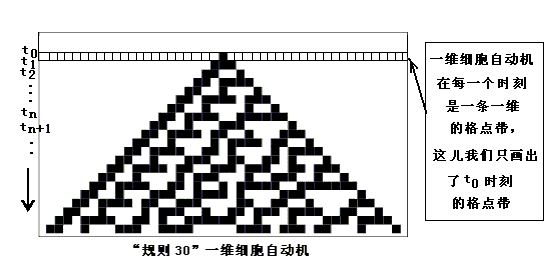
木匠眼裡的月亮

-     沃爾弗拉姆和他的‘新科學’

西方有句諺語：“在木匠眼裡，月亮也是木頭做的。”

古希臘哲學家泰勒斯說：萬物之本是水。他的學生畢達哥拉斯說：萬物之本是數。看來，哲學家和木匠異曲同工，都希望把複雜的世界追根朔源到某一種簡單的東西。

如今這個計算機時代，有人說：萬物之本是計算。

這個人就是上世紀80年代後期開發著名的《數學》Mathematica符號運算軟件的美國計算機科學家，史蒂芬·沃爾弗拉姆(Stephen Wolfram)。

實際上，沃爾弗拉姆並不是提出“萬物之本是計算”的第一人。MIT計算機實驗室前主任弗雷德金，早在上世紀80年代初就提出：“終極的實在不是粒子或力，而是根據計算規則變化的數據比特。”著名物理學家費曼在1981的一篇論文裡也表達過類似的觀點。

不過，沃爾夫勒姆沿着這條路走得更遠。從古至今困擾人們的三個基本哲學問題：生命是什麼？意識是什麼？宇宙如何運轉？按照沃爾夫勒姆在他的“新科學”里的“計算等價原理”，生命、意識都從計算產生，宇宙就是一台‘細胞自動機’。

被人們稱為天才的沃爾弗拉姆一九五九年生於倫敦，十五歲發表他的第一篇科學論文，二十歲獲得美國加州理工學院的物理博士學位。之後，又榮獲麥克阿瑟基金會的“天才”獎。當時，他將此獎項所獲得的十二萬五千美元的獎金全部用於了他感興趣的基本粒子物理及宇宙學等方面的研究。

八十年代初期，即將離開加州理工學院，前往普林斯頓高等研究院進行研究的沃爾弗拉姆在一次研討會上，初識了“細胞自動機”的理論，頗有一見鍾情、相見恨晚的樣子，一頭扎進細胞自動機的研究之中。

我們在另一篇文章中介紹過的生命遊戲，其實就是是二維的細胞自動機。除了二維情況之外，我們還可以研究一維、三維、甚至更多維的細胞自動機。一般地說，不管是研究多少維的細胞自動機，首先都得作好如下一些規定：

1.           將空間分成許多小格子（細胞），比如一維細胞自動機，是把直線分成相等的許多等分；二維細胞自動機，是把平面分成許多正方形或六邊形網格；三維細胞自動機，是把空間劃分出許多立體網格。

2.           規定每個格子可取多少種狀態，如“0/1”，或更多種（k種）。

3.           規定每個格子有哪些鄰居，即與其有“關係”的格子。

4.           時間也被分成一系列離散的時間間隔，或者，叫做“代”。

5.           規定格子狀態在不同時間間隔的變化規則。

經過每一個時間間隔，網格中的格點狀態按照所定的規則同步地更新，更新的狀態由格點自身和四周鄰近格點在前一時刻的狀態共同決定。因此，如果在以上規定中變換各種情況，例如採取不同的格子形狀、不同的狀態集、不同的鄰居定義、或不同的操作規則，都將構成不同的細胞自動機。

因為生命遊戲是二維的細胞自動機，還不是最簡單的。最簡單的細胞自動機當然是對於上述的每條規定，都取最簡單的情形，那就是一維細胞自動機：

1.  維數為一，這種一維細胞空間可以用一條無限長的格點帶來表示；

2.  每個細胞只有兩種狀態，用每個格子或黑或白表示細胞的狀態；

3.  如何定義相鄰細胞呢？就一維的一般情況來說，可以考慮距離每個細胞r個細胞以內細胞的影響，最簡單是r=1，也就是只考慮與其相接的“左”、“右”兩個鄰居的影響；

現在，讓我們稍微詳細一點研究一維細胞自動機。為了顯示一維細胞自動機中，細胞狀態不同瞬時的演化情況，我們將每一個相繼時刻對應的的格點帶附在上一時刻對應的的格點帶下面。例如，下面所示的圖中，我們可以看到：在t0時刻的格點帶，是一條只有中間一個格點為‘黑’，其餘格點均為‘白’的左右延伸的長帶子。

一維細胞自動機的例子：規則30 

上圖中，除了時刻t0之外，沒有顯示出其它時刻的所有格點，但仍然畫出了狀態為‘黑’的格點。也就是說，上圖顯示的是一維細胞自動機的格點狀態隨時間變化的情形。如圖所示，垂直向下的方向表示時間的流逝。因為加了一個時間軸，所以，雖然是一維細胞自動機，而計算機屏幕顯示出來的卻是一個二維格點圖。

 滿足如上條件的最簡單的細胞自動機被稱為初級細胞自動機。迄今為止，我們尚未討論它們的時間演化規律。實際上，上圖顯示的只是符合某一種時間演化規律的一維細胞自動機。如果我們定義了另一種時間演化規律，就會得到另一種二維格點圖，也就是說，就定義了另一種一維細胞自動機。那麼，到底有多少種初級的一維細胞自動機呢？

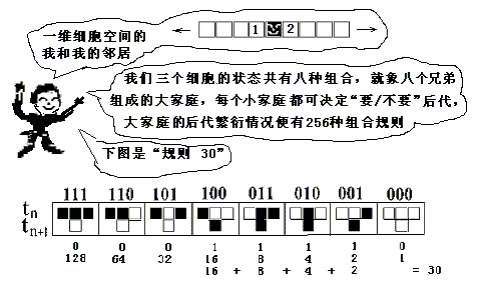
我們可以按照如下的考慮來定義時間演化規律：因為每個細胞有兩個鄰居，加上自己，共有三個相鄰細胞，好比是：我、你、他。因此，‘我’這個細胞下一個時刻的狀態便由‘我’‘你’‘他’這三個相鄰細胞此一時刻的八種狀態的組合所決定。

圖二  規則30

如上圖所示，在每一種組合情況下，都有兩種方式來規定中間細胞下一個時刻的狀態：‘黑’或‘白’（生或死）。因此，八種組合則能定義出2⁸=256種不同演化規律的一維細胞自動機，每一種自動機正好對應於一個八位的二進制數，當然，也可以說對應於一個0和255之間十進制數，我們就把這個數作為一維細胞自動機的標誌，稱為“規則數”。從圖二中的下面部分，可看出“規則 30”是如何定義的。對於每一種規則，還可以給每一個格點設置不同的初始態，最簡單的初始態設置方法是假定只有位於中心的一個細胞的狀態為“生”（黑色），而其餘細胞均為白色。圖四給出了部分初級一維細胞自動機在簡單初始情況下的時間演化圖案（圖案下顯示的是“規則數”）。

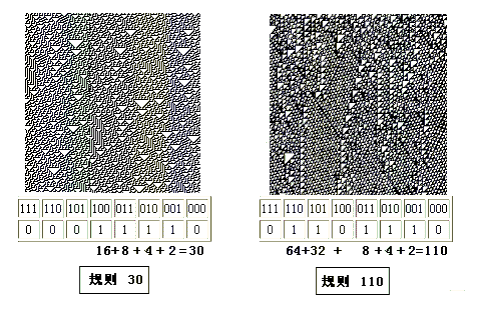
在沃爾弗拉姆發表的一系列論文中，對一維細胞自動機的代數、幾何、統計性質作了系統深入的研究和分類。他還特別對其中初級細胞自動機的“規則 30”和“規則 110”的有趣性質情有獨鍾。圖三給出這兩種規則對於隨機初始值的時間演化圖。“規則 30”的細胞自動機之所以特別是因為它的“混沌”行為，例如我們可以考查中心細胞的狀態隨時間演化所得到的二進制序列：1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, ...，可以證明，這是一個無窮不循環的偽隨機序列。“規則 110”則更為有趣：在隨機的初始條件下，卻產生出好些看起來在一定程度上“有序”、但是又永不重複的圖案。“規則 110”似乎揭示了無序中的有序, 混沌之中包含着的豐富的內部結構,  隱藏着更深層次的規律。沃爾弗拉姆的一個年輕助手庫克後來（1994年）證明，“規則 110”是等效於通用圖靈機的。

圖三  規則30和規則110

如何來理解一個細胞自動機“等效於通用圖靈機”呢？可以按照如下思路直觀地理解這點：從前面的敘述我們已經知道，象圖三中“規則 30/110”這樣的一維細胞自動機的二維圖案，是由許多一條一條的、左右方向無窮長的格點帶，或者說“符號串”，從上到下延伸而構成的。每一條格點帶都對應於一個離散的時刻，最頂上的一條對應於初始時刻，然後，時間流逝，格點帶逐條顯現。因此，可以想象，如果我們有適當的編碼方法，就能將任何數學問題，包括它的初值和算法，變成一列符號串，寫到這初始的第一條上。然後，根據細胞自動機內定的變換規則，可以得到下一時刻的符號串，也就是說，完成了一次“計算”。依此類推，時間不斷地前進，“計算”便一步一步地進行，直到所需要的結果。然而，不同規則的細胞自動機，則可以看成具有不同的“計算”能力。

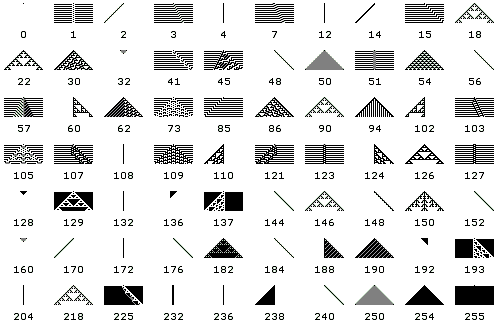
圖四  規則0-規則255的演化圖案

例如，讓我們考查一下圖四所顯示的256個初級細胞自動機中的幾個特例：

1.    首先，象“規則 255”這樣的，完全談不上什麼計算能力，連“識別”能力都沒有，因為無論對什麼“數”，經它“計算”一次之後，全部一抹‘黑’，這點從它的規則定義也可看出來；“規則0”也一樣，全部一抹‘白’。

2.    接着，我們再來看象“規則 90”那一類的，時間演化圖有點象帕斯卡三角形的那種。這種情況的結果太規矩了，肯定計算能力有限，第一條的數據再複雜，猶如“對牛彈琴”一樣。

3.    另外，象“規則 30”那樣的，似乎較好一些，但邏輯雜亂無章。

4.    最後，唯有像“規則 110”這樣的，計算能力才達到標準，被證明與通用圖靈機是計算等效的。

上世紀八十年代後期，沃爾弗拉姆以開發了著名的《數學》符號運算軟件而聲名大振，且獲得了商業上的成功。進入九十年代後，他便躲進小樓，繼續他所痴迷的細胞自動機工作，特別是對“規則 110”的研究。事實上，起初，沃爾弗拉姆並不認為“規則 110”能與通用圖靈機等效，當庫克證明這點之後，沃爾弗拉姆又阻止、拖延庫克的文章的發表，因為他正在潛心著作一部“曠世之作”。直到2002年，沃爾弗拉姆奮戰10年，經過無數次的敲鍵盤、移鼠標，終於產生出作者狂妄地自我宣稱是“與牛頓發現的萬有引力相媲美的科學金字塔”的巨著，名為：《一種新科學》。

在這部1200頁的重量級著作中，沃爾弗拉姆將他所偏愛的“規則 110”的精神光大發揚，貫穿始終。根據書中的觀點，各種各樣的複雜自然現象，從彈子球、紙牌遊戲到湍流現象；從樹葉、貝殼、等生物圖案的形成，到股票的漲落，實際上都受某種運算法則的支配，都可等價於“規則 110”細胞自動機。沃爾弗拉姆認為“如果讓計算機反覆地計算極其簡單的運算法則，那麼就可以使之發展成為異常複雜的模型，並可以解釋自然界中的所有現象”，沃爾弗拉姆甚至更進一步地認為宇宙就是一個龐大的細胞自動機，而“支配宇宙的原理無非就是區區幾行程序代碼”。

 《一種新科學》的出版在當時引起轟動，初版五萬冊在一星期之內銷售一空，但是，學術界大多數專家們對此書的評價卻不高。對沃爾弗拉姆傲慢自大、忽視前人的工作、自比牛頓的做法，有些評論者更是嗤之以鼻，認為這是使用商業手段，對不熟悉細胞自動機的廣大讀者的一種誤導。事實上，沃爾弗拉姆並未創立什麼“新科學”，細胞自動機的理論，已有五十多年的歷史，這個理論，以及基於複雜源於簡單的道理的‘複雜性科學’，一直都是麻省理工學院弗雷德金等人的研究課題。沃爾弗拉姆的“宇宙就是一個細胞自動機”等之類過甚其詞的、計算機萬能論的、並未給出證據的“假設”，也是源於他人。

 難怪諾貝爾獎獲得者溫伯格打趣地說：“在木匠眼裡，月亮也是木頭做的。”