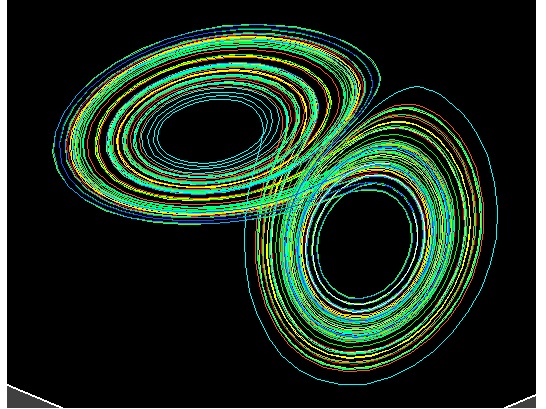| 天蓉:《走近混沌》-12-洛倫茨的迷惑 |
| 送交者: 天蓉 2012年09月24日15:12:57 於 [教育學術] 發送悄悄話 |
|
第十二章:洛倫茨的迷惑
李四洋洋灑灑地高談闊論了一番,張三笑起來了,說李四犯了和他的物理界老祖宗們一樣的毛病,把物理當成哲學了。物理畢竟不是哲學,你還是給我們講一些具體點的東西吧,講與你的那個X教授做的課題有點關係的。
李四扶正了帶着的深度近視眼鏡,仍然不緊不慢的,一邊打開一本書,一邊說,這不馬上就要進到正題了嗎∶經典力學為何導出了決定論? 混沌理論又是怎樣證明一個決定論的系統也可以出現隨機的行為的呢? 你們看,當我們翻開任何一本關於混沌數學的書, 差不多都能看到與圖(12.1)類似的圖案。那是混沌理論的著名標籤∶‘洛倫茨吸引子’:
“什厶是‘吸引子’啊?”王二問。
李四摸了摸大腦袋說∶“你的問題提得好啊,不過,‘吸引子’這個題目超前了一點兒,以後再講。今天,我先講講這個圖的來由,講講洛倫茨的工作吧┅┅”
愛德華·洛倫茨(1917-2008)是一位在美國麻省理工學院做氣象研究的科學家。上世紀的60年代初, 他試圖用計算機來模擬影響氣象的大氣流。當時,他用的還是由真空管組成的計算機,那是一個充滿整間實驗室的龐然大物啊。我想,那機器雖然大,計算速度還遠不及我們現在用的這些電腦吧。所以,可想而知,洛倫茨沒日沒夜的,工作得很幸苦。嚴謹的科學家不放心只算了一次的結果, 決定再作一次計算。為了節約一些時間, 他對計算過程稍微作了些改變,決定利用一部分上次得到的結果, 省略掉前一部分計算。
因此,那天晚上,他辛辛苦苦地工作到深夜,直接將上一次計算後的部分數一個一個打到輸入卡片上,再送到計算機中。好,一切就緒了,開始計算!洛倫茨才放心的回家睡大覺去了。
第二天早上,洛倫茨興致勃勃地來到MIT計算機房,期待他的新結果能驗證上一次的計算。可是,這第二次計算的結果令洛倫茨大吃一 ∶他得到了一大堆和第一次結果完全不相同的數!結果1和結果2千差丌別!
這是怎厶回事呢?洛倫茨只好再計算一次,結果仍然如此。又再回到第一種方法,計算後得到原來的結果1。洛倫茨翻來覆去地檢查兩種計算步驟,又算了好幾次,方法1總是給出結果1,方法2總是給出結果2。兩種結果如此大大不同,必定是來自於兩種方法的不同。但是,兩種方法中,最後的計算程序是完全一樣的,唯一的差別是初始數∶第一種方法用的是計算機中存儲的數,而第二種方法用的是洛倫茨直接輸入的數。
這兩組數應該一模一樣啊!洛倫茨經過若干次的檢查和驗證,盯着一個一個的數字反反覆覆看。啊,終於看到了。兩組數的確稍微有所不同,若幹個數中,有那厶幾個數字,被四捨五入後,有了一個微小的差別。
難道這厶微小的差別(比如,.000127)就能導致最後結果如此大的不同嗎?洛倫茨百思而不解。
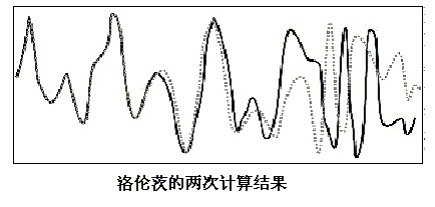
圖(12.2)∶實線和虛線分別是洛侖茲的兩次計算過程∶ 初始值的微小差別,導致最後的結果完全不同。資料來自於(Ian Stewart, Does God Play Dice? The Mathematics of Chaos, pg. 141)
上面的示意圖中,顯示的是與洛倫茨氣象預報研究有關的結果。其中橫坐標表示時間,縱坐標表示洛倫茨所模擬,也就是想要預報的氣候中的某個參數值,比如說,大氣氣流在空間某點的速度、方向,或者是溫度、濕度、壓力之類的變量等等。根初始值以及描述物理規律的微分方程,洛倫茨對這些物理量的時間演化過程進行數字模擬,以達到預報的目的。但是,洛倫茨發現,初始值的微小變化,會隨着時間增加而被指數放大,如果初始值稍稍變化,就使得結果大相徑庭的話,這樣的預報還有實際意義嗎?
王二似乎恍然大悟∶“啊,難怪氣象台播的氣象預報經常都不准,招來罵聲一片,看來他們也有他們的苦衷啊!”
張三說,圖(12.2)這個曲線的意思比較容易理解,但是那個圖(12.1)是怎厶得來的啊?我看它沒完沒了的繞圈圈,這與洛倫茨的氣象預報計算有什厶關係呢?
李四說,慢慢聽,當然有關係!當時的洛倫茨雖然甚感迷惑,卻未必見得認識到了這個偶然發現的重要性, 也不一定能想到與此相關的‘混沌型’解將在非線性動力學中掀起一場軒然大波。儘管如此,洛倫茨畢竟是一位數學訓練有素的科學家。實際上,洛倫茨年輕時在哈佛大學主修數學,只是因為後來爆發了第二次世界大戰,他才服務於美國陸軍航空隊,當了一名天氣預報員。沒想到經過戰爭中這幾年與氣象打交道的生涯,洛倫茨喜歡上了這個專業。戰後,他便改變方向,到MIT專攻氣象預報理論,之後又成為了MIT的教授。他要利用他的數學頭腦,還有當時剛剛初露鋒芒的計算機和數字計算技術,來更準確地預測天氣,這是洛倫茨當時夢寐以求的理想。
可是,這兩次計算結果千差丌別,這種結果對初始值的分外敏感性給了洛倫茨的美好理想當頭一棒!使洛倫茨覺得自己在氣象預報工作中似乎顯得山窮水盡、無能為力。為了走出困境,他繼續深究下去。然而,越是深究下去,越是使洛倫茨不得不承認他的“準確預測天氣”的理想是實現不了的!因為當他研究他的微分方程組的解的穩定性時,發現一些非常奇怪和複雜的行為。
洛倫茨以他非凡的抽象能力, 將氣象預報模型里的上百個參數和方程, 簡化到如下一個僅有三個變量及時間的、係數完全決定了的微分方程組。
dx/dt = 10(y - x) (12.1) dy/dt = R*x ˉ y ˉ xz (12.2) dz/dt = (8/3)z + xy (12.3)
這兒方程組中的x,y,z,並非任何運動粒子在三維空間的坐標,而是三個變量。這三個變量由氣象預報中的諸多物理量,如流速、溫度、壓力等等簡化而來。方程(12.2)中的R在流體力學中叫做瑞利數,與流體的浮力及粘滯度等性質有關。瑞利數的大小對洛侖茲系統中混沌現象的產生至關重要,以後還要談到。
這是一個不能用解析方法求解的非線性方程組。洛侖茲將瑞利數R=28,然後,利用計算機進行反覆迭代, 即首先從初始時刻x、y、z的一組數值x0、y0、z0,計算出下一個時刻它們的數值x1、y1、z1,再算出下一個時刻的x2、y2、z2┅┅如此不斷地進行下去。將逐次得到的x、y、z瞬時值, 畫在三維坐標空間中,這便描繪出了圖(12.1)的奇妙而複雜的‘洛倫茨吸引子’圖。
下一篇∶奇異吸引子 |
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | WWDC2011視頻的學習筆記(19) | |
| 2010: | 貼一下罵方挺肖的白痴是如何自扇耳光的 | |
| 2010: | 紫荊棘鳥先生,樓下回你,怕你看不到。 | |
| 2009: | 歐陽山甲:霍金:一切都是註定的嗎? | |
| 2009: | 基甸恩典:從霍金的演講談談科學主義的 | |
| 2008: | 高房價拖垮中國經濟的初步風險分析 | |
| 2008: | 收入萬寶的這篇文章, 是為了和陳志武 | |