| 天蓉:《走近混沌》-14-蝴蝶效應 |
| 送交者: 天蓉 2012年10月07日14:33:25 於 [教育學術] 發送悄悄話 |
|
第十四章:蝴蝶效應
“圖(13.1)中,右邊的洛侖茲吸引子,看起來就顯然不同於那幾個經典的。不屬於經典理論的吸引子,就叫做奇異吸引子,對吧?”張三問。
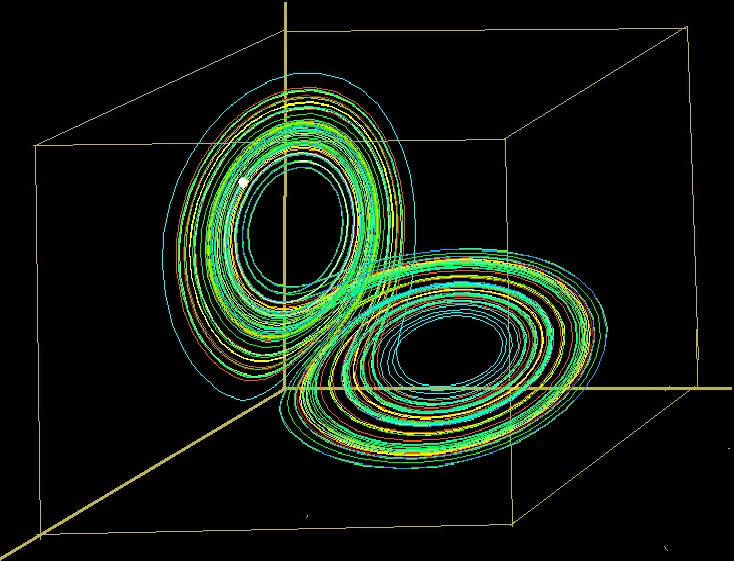
對,但是我們還是得從數學上弄明白,奇異吸引子到底有哪些特別之處。我們在前一章中提到過∶幾個經典吸引子分別是0、1、2維的圖形。那你們看看,下面圖中這個畫在3維空間的洛侖茲吸引子像是多少維呢?
“多少維?”王二眼睛一亮∶“這個維數一定是個分數?”
圖(14.1)∶洛倫茨吸引子是個2.06維的分形 http://www.tianfangyetan.net/cd/java/Lorenz.html
張三想了想說∶“等等,這個圖形的確像一個分形。但是分形的維數不一定就是分數。圖形雖然複雜,但是看起來,每個分支基本上都還是在各自的平面上轉圈圈。總共是兩個平面,這個圖形可能還是2維。有點類似分形龍的圖形那樣,曲線繞來繞去,繞來繞去,最後充滿一部分面積┅┅所以我猜是2維。”
從前幾章對分形的介紹中, 我們已經知道: 不僅有整數維的幾何圖形,也有分數維的幾何形狀存在。表現出‘混沌現象’的系統的吸引子-奇異吸引子,就是一種分形。整數維數的吸引子(正常吸引子)是光滑的周期運動解,分數維數的吸引子(奇異吸引子)則是相關於‘非線性系統’的非光滑的混沌解。圖(14.1)所示的洛倫茨吸引子的曲線, 只是象徵性地顯示了曲線的一部分。吸引子實際上是一個具有無窮結腹的分形。如讀者點擊圖(14.1),鏈接到‘洛倫茨吸引子’程序, 進一步觀察, 則會發現, 狀態點, 也就是洛倫茨系統的解, 將隨着時間的流逝不重複地, 無限次數地奔波於兩個分支圖形之間。有數學家仔細研究了洛倫茨吸引子的分形維數,得出的結果是2.06(+、-)0.01。
從奇異吸引子的形狀及幾何性質,我們看到了混沌和分形關聯的一個方面∶分形是混沌的幾何表述。
奇異吸引子不同於正常吸引子的另一個很重要特徵是它對初始值的敏感性∶前面一章中所說的三種經典吸引子對初始值都是穩定的, 也就是說, 初始狀態接近的軌跡始終接近,偏 不遠。而奇異吸引子中,初始狀態接近的軌跡之間的距 卻隨着時間的增大而指數增加。
這就是為什厶使得在數學上造詣頗深的洛倫茨迷惑的原因。因為他發現,用他的數學模型進行計算的結果大大地違背了經典吸引子應有的結論。因為給定初始值的微小差別,而使得結果完全不同。計算結果隨着被計算的天氣預報的時間, 成指數地放大, 在他所計算的兩個月的預報之中, 每隔四天的預報計算, 差別就被放大一倍。因此,最後得到了顯然不同的結果。
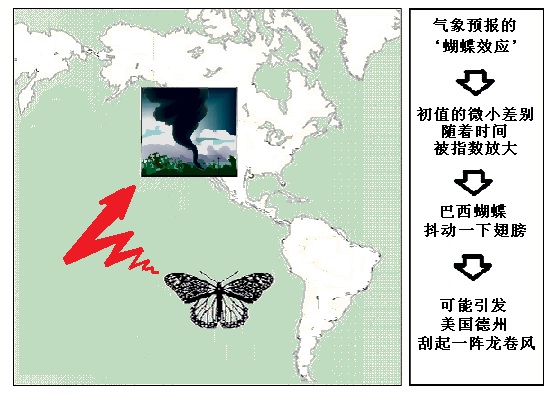
由此, 洛倫茨意識到,‘長時期的氣象現象是不可能被準確無誤地預報的’。因為,計算結果證明∶初始條件的極微小變化, 可能導致預報結果的巨大差別。而氣象預報的初始條件, 則由極不穩定的環球的大氣流所決定。這個結論被他形象地稱為‘蝴蝶效應’,用以形容結果對初值的極其敏感。意思是說,只是因為巴西的一隻蝴蝶抖動了一下翅膀,而改變了氣象站所掌握的初始資料,三個月之後,就有可能引發美國德克薩斯州出乎意料之外地颳起一陣未曾預報到的龍捲風。用中國人的術語來說,則叫做∶‘差之毫厘, 失之千里’也。
圖(14.2)∶‘蝴蝶效應’示意圖
王二笑着說∶“好像也有人說,叫做蝴蝶效應是因為洛侖茲吸引子的圖看起來很像兩個抖動的蝴蝶翅膀。不管怎厶樣,我喜歡這個名字,這個名字也啟發了文學藝術家們無限的想象,產生出不少作品┅┅”
‘洛倫茨吸引子’是第一個被深入研究的‘奇異吸引子’。洛倫茲模型是第一個被詳細研究過的可產生混沌的非線性系統。
張三說∶“具有‘奇異吸引子’的系統應該是比較少的特例吧?我記得在洛倫茨的方程組中有一個叫瑞利數的參數R,當R=28的時候,方程才有混沌解。在許多別的R值,哈哈,巴西的蝴蝶煽動不煽動翅膀都沒關係的!”
這是一個誤解。其實, 象洛倫茨發現的這類具有‘奇異吸引子’的系統並非什厶鳳毛麟角的例外,而是自然界隨處可見的極普遍的現象,是經典力學所描述的事物的常規。然而,經典力學已建立三百多年, 為什厶經典系統的混沌現象卻直到三十多年前才被發現呢? 這其中的原因不外乎如下幾點: 一是人們的觀念上總是容易被成熟的, 權威的理論所束縛; 二則又是與近二, 三十年來計算機技術的飛速進展分不開的。洛倫茨吸引子被發現之後, 許多類似的研究結果也相繼問世。有趣的是,各個領域的科學家還紛紛抱怨說他們早就觀測到諸如此類的現象了。可是當時,或是得不到上司的認可, 或是文章難以發表, 或是自己以為測量不夠精確, 或是認為由於噪聲的影響, 等等等等。總而言之,各種原因,使他們失去了千載難逢的第一個發現奇異吸引子,發現混沌現象的機會。
王二提出一個使他迷惑的問題∶“剛才說到∶奇異吸引子的行為廣泛地存在於經典力學所描述的現象中。這句話是什厶意思啊?奇異吸引子不是與經典吸引子不同嗎?”
李四說∶“這兒,‘經典’這個字用得有點混淆。本來,所謂經典物理,是指有別於量子物理而言。奇異吸引子與量子物理是兩回事。比如說吧,洛倫茨得到的微分方程組,是從經典物理理論、經典力學規律得到的方程組。既不是隨機統計的,也與量子理論無關。但是,這種符合經典理論的方程卻有混沌行為的解。”
奇異吸引子的行為廣泛地存在於經典力學所描述的現象中,存在於各類非線性系統中。由於‘奇異吸引子’和 ‘混沌行為’是非線性系統的特點,這些發現,又將非線性數學的研究推至高潮。上個世紀的八十年代,九十年代,各門傳統學科都在譜寫自己的非線性篇章,即使在人文,社會學的研究系統中也發現了一批奇異吸引子和混沌運動的實例。因此,混沌理論的創立與牛頓的經典理論發生衝突,給了決定論致命的一擊,拉普拉斯妖也無能為力了。
張三卻仍然固執己見,說∶“蝴蝶效應雖然說明了某些情況下,結果對初值非常敏感,但是,這並不等於就否定了決定論啊!比如說到洛倫茨的天氣預報吧,由於混沌現象的產生,目前的計算技術使他的誤差在四天后增加一倍,但是如果將來計算機的速度加快、精度提高,對初始值也測量得更準確,就可能使得誤差在四十天、或四百天后,才增加一倍,這不就等於能‘準確預報’了嗎?我覺得世界還是決定論的,只是計算及測量的精度問題┅┅”
王二不同意,但卻反駁不到點子上,他只是堅信決定論是不對的∶
“怎厶可能像拉普拉斯妖所說那樣,這個世界,還有你、我、他,將來的一切都被決定了呢?我們三個人此時此刻說的每一句話都在大爆炸的那個時刻就決定了,這聽起來太荒謬絕倫了吧。事情的發展太多偶然因素,不可能都是命中注定的┅┅”
張三大笑∶“你那天不是還在朗誦一首詩,說林零是你命中注定的愛人嗎┅┅” 王二急了∶“唉,你不懂,那是情感的宣泄、文學的東西┅┅不是科學┅┅”
李四則認為,數學解決不了決定論還是非決定論的問題。就物理學的角度而言,起碼有兩點證,不支持決定論。一是已經有100多年歷史的量子理論的發展。量子物理中的不確定原理表明∶位置和動量不可能同時確定,時間和能量也不可能同時確定。因此,初始條件是不確定的,永遠不可能有所謂‘準確的初始條件’,當然,結果也就不可能確定。這是其一。
另外,經典的物理規律,大多數都是用微分方程組的數學模型來描述的。建立微分方程的目的,本來就是為了研究那些確定的、有限維的、可微的演化過程。因此,微分方程的理論是機械決定論的基礎。但是,微分方程組不一定就真是描述世界的最好方法,事實上,在牛頓力學以外的大部分物理學,不能只用微分方程來研究,而對大自然中廣泛存在的分形結腹、物理中的湍流、布朗運動、生命形成過程,等等,微分方程理論更是力不從心。既然作為決定論基礎的微分方程並不能用來解決世界的大多數問題,“皮之不存,毛將焉附”。基礎沒有了,決定論失去了依託,拉普拉斯妖還有話說嗎?恐怕只能躲在天國里唉聲嘆氣了! 下一篇∶龐加萊
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | 物理學現在確實變成玄學了,不是爆炸就 | |
| 2011: | YDX:蘋果與宇宙膨脹 | |
| 2010: | 回遊的海歸:聲援饒毅和施一公 | |
| 2010: | 方舟子打假的本質 | |
| 2009: | ZT/漢語是世界上唯一一種面向對象的高 | |
| 2009: | 迄今還沒一個本土純用漢字的國人獲諾貝 | |
| 2008: | 看,一個“知名”科學騙子! | |
| 2008: | 又是楊-米爾斯理論 | |