| 天蓉:《走近混沌》-20-混沌魔鬼不穩定 |
| 送交者: 天蓉 2012年12月05日15:14:24 於 [教育學術] 發送悄悄話 |
|
第二十章﹕混沌魔鬼‘不穩定’
王二正在總結他的演講,談到他計劃中的畢業論文課題:
“你們知道,我們這個由各類生物群體組成的大千世界,盤根錯節、繁雜紛紜;天下萬物,互相制約、互相依存;自然界中形形色色的動植物不停地出生、繁殖、變化、死亡,時而大浪淘沙、優勝劣汰;時而又相輔相成、維持平衡。在永不間斷的爭爭鬥斗、生生死死中, 各種生物群體的數目變化莫測,有時侯表現一定程度的周期性, 有時侯又貌似一片混沌,的確有些類似於上兩章中所研究的邏輯斯蒂方程的解的行為。我正在想,用邏輯斯蒂方程為基礎,是否可能找出一個描述包括多種生物競爭,群體數如何變化的生態模型來……”
王二的想法引起了好幾個生物相關專業學生的興趣,他們聚在一起開始熱烈討論生態學的問題。
其實,邏輯斯蒂方程不僅在生態研究方面意義重大,在別的領域也有諸多應用。是啊,邏輯斯蒂映射看起來太簡單了,只有1個變量,1個方程,卻能表現出混沌系統的種種特徵。還記得我們曾經討論過的其它混沌系統,比如洛倫茨系統和三體問題嗎?相對於它們的原始問題來說,最後的方程也算夠簡單了,但是,仍然有三個變量、三個微分方程。
混沌理論的老祖宗龐加萊曾經提出一個定理,稍後被瑞典數學家本迪克松證明,說的是混沌現象只能出現在三維以上的連續系統中。但這個定理不適用於離散系統,邏輯斯蒂迭代方程所描述的就是一個特別簡單的1維離散系統。混沌魔鬼在這個簡單系統中輕巧地跳出來,成為混沌研究者們的最愛。
李四對此深有體會,因為他正在做一個與流體力學、湍流等有關的課題,涉及的系統很複雜。當系統維數太多想不清楚時,李四就總是回到最簡單的一維邏輯斯蒂方程,用圖形的方法來考慮問題,感覺容易多了。不過,張三今天卻說:
“總的來說,1個變量的確比3個變量簡單很多。不過,有時候,3維的圖像也挺直觀的。比如說你看,當我用計算機畫奇異吸引子的時候,畫出來的洛倫茨吸引子多漂亮!洛倫茨方程的解,是隨時間變化而無限繞下去、卻又永不重複的軌道,在三維空間中畫出來,好像一隻翩翩起舞、展翅欲飛的蝴蝶。可是,這個邏輯斯蒂方程的吸引子,用圖形表示就不好看了。”
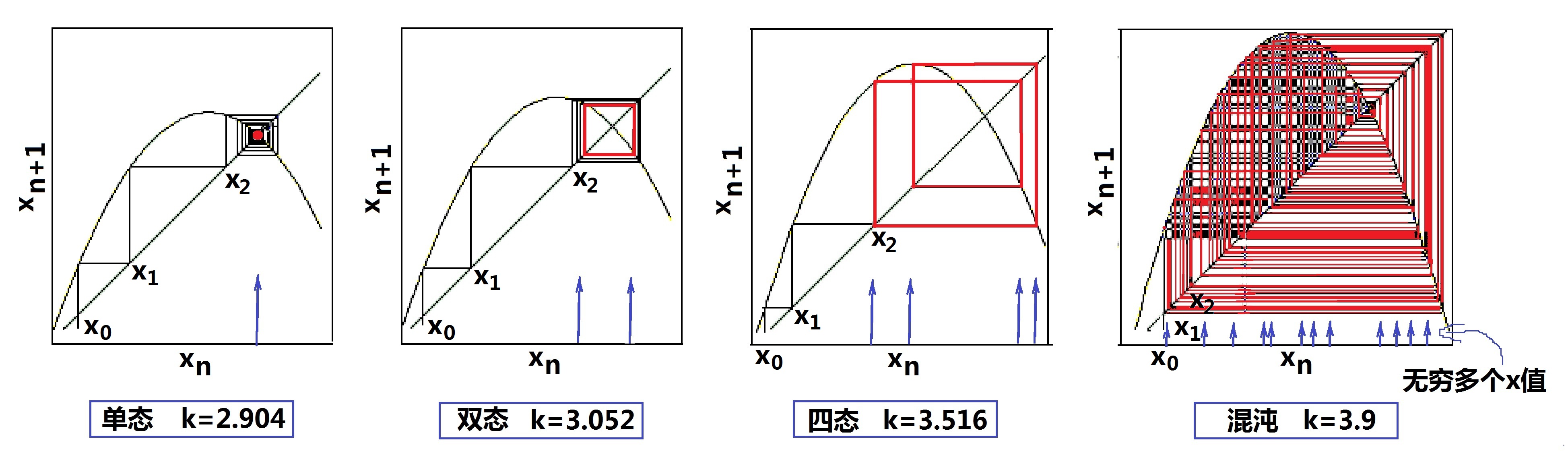
張三的說法不無道理。對邏輯斯蒂方程來說,每個不同的k值都有一個吸引子,在‘平衡’區域,吸引子是1個固定點;在‘雙態平衡’區域,吸引子是2個固定點;在‘多態平衡’區域,吸引子是多個分離的固定點;而在‘混沌’區域,吸引子是連成一片的點;最後的狀態在這些點無規律地蹦來蹦去,到底是如何蹦的?分岔圖上對具體過程顯示得並不清楚。不過,我們可以用如圖(20.1)所示的邏輯斯蒂迭代圖,清楚地看到在不同k值下,迭代過程中xn的收斂情形。
圖(20.1)中,標為紅色的是迭代的最後過程。圖中的拋物線對應於邏輯斯蒂方程右邊的非線性迭代函數(xn+1 = kxn·(1-xn))。 從左向右看:第一個小圖中的xn最後收斂於一個紅點;第二個小圖中的xn最後收斂於一個紅色矩形,標誌着有兩個不同的x值;而第三個小圖中的xn最後收斂的紅色區域,是在4個不同的x值中循環;最右邊的‘混沌’情況,大家一看圈來圈去的紅色曲線便明白了:有點類似於洛倫茨的蝴蝶圖了,這是魔鬼現身的表現!
圖(20.1):不同k值下的邏輯斯蒂迭代圖
邏輯斯蒂系統還有一個少有的優點:它所對應的微分方程可以求得精確的解析解。而大多數非線性系統是無法得出精確解的,只能用迭代法來研究數值解的定性性質,以及解的穩定性。
混沌魔鬼的出現,與參數k的數值有關,k越大,魔鬼出現的幾率就越大。這其中有何奧秘呢?我們回到邏輯斯蒂方程描述的生態學,回憶一下參數k的意義是什麼?k是群體數的線性增長率,與出生率有關。想到這點,我們恍然大悟:如果k比較大,群體繁殖得太多了,數目增長太快,增加社會不穩定的因素,當然就容易造成混亂,令魔鬼現身囉。
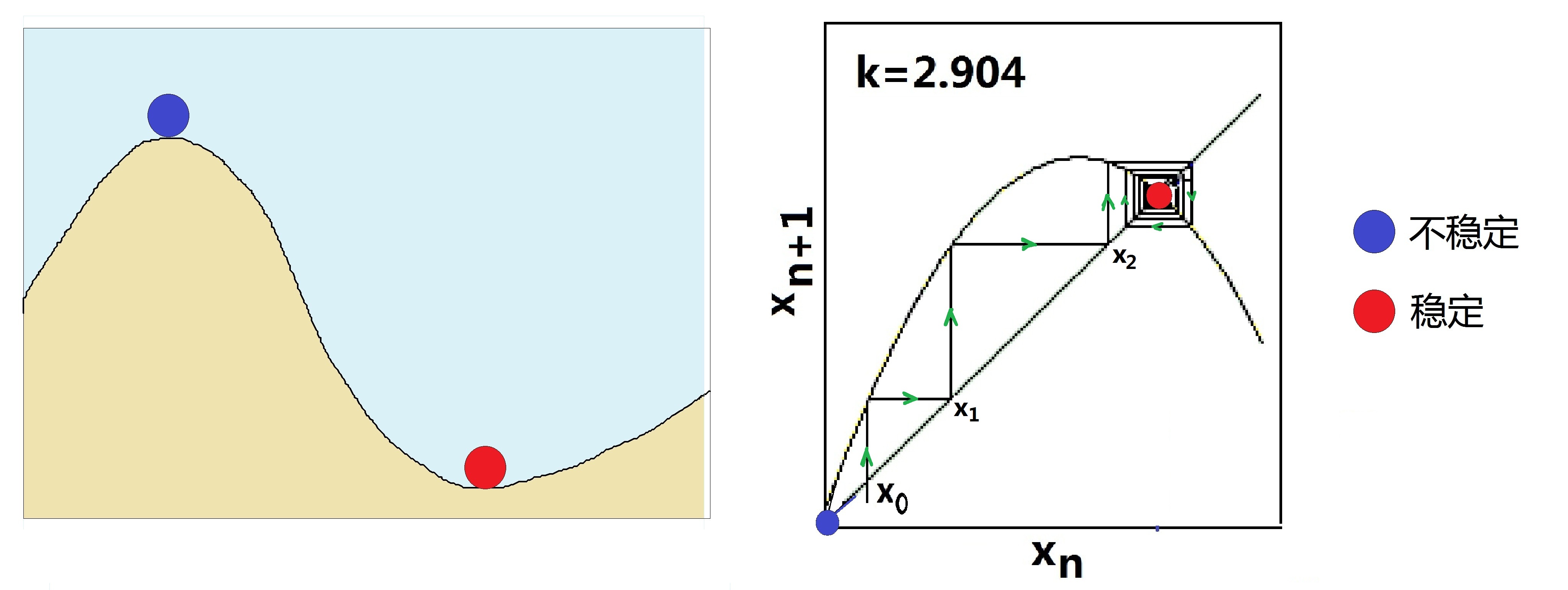
圖(20.2):不穩定和穩定
混沌的產生的確與方程的‘穩定性’有關,因此,我們有必要討論討論系統狀態的穩定性。哪種狀態是穩定的?哪種狀態是不穩定的?從圖(20.2)的左圖中一目了然,那是在重力場中‘穩定’和‘不穩定’的概念:對小圓球來說,坡頂和坡谷都是重力場中可能的平衡狀態。但是人人都知道,位於頂點的藍色球不穩定,位於谷底的紅色球很穩定。究其根源,是因為只要藍色球開始時被放斜了那麼一丁點兒,就會因不能平衡而掉下去。而紅球呢,則不在乎這點起始小誤差,它總能夠滾到谷底而平衡。用稍微科學一點的語言來說,穩定就是對初值變化不敏感,不穩定就是對初值變化太敏感。我們將這個意思發揮擴展到邏輯斯蒂方程上,考慮圖(20.2)的右圖中k=2.9時,即吸引子是一個固定點的情況。這時,邏輯斯蒂方程的解應該是圖中的拋物線和45度直線的交點,圖中的這兩條線有兩個交點。因此,除了固定吸引子x無窮=0.66之外,x無窮=0也是一個解。但是,在圖中所示的條件下,x無窮=0.66是穩定的解,x無窮=0卻是不穩定的解。為什麼呢?因為只要初始值從0偏離一點點,像圖中所畫的情況,迭代的最後結果就會一步一步地遠離0點,沿着綠色箭頭,最終收斂到x無窮=0.66這個穩定的平衡點。
研究三體問題的大數學家龐加萊,是微分方程定性理論的始創者。有關微分方程解的穩定性問題,則由另一位數學家李亞普洛夫始開先河。亞歷山大·李亞普洛夫(1857-1918)是與龐加萊同時代的俄國數學家和物理學家。與穩定性密切相關的李亞普洛夫指數,便是以他命名。
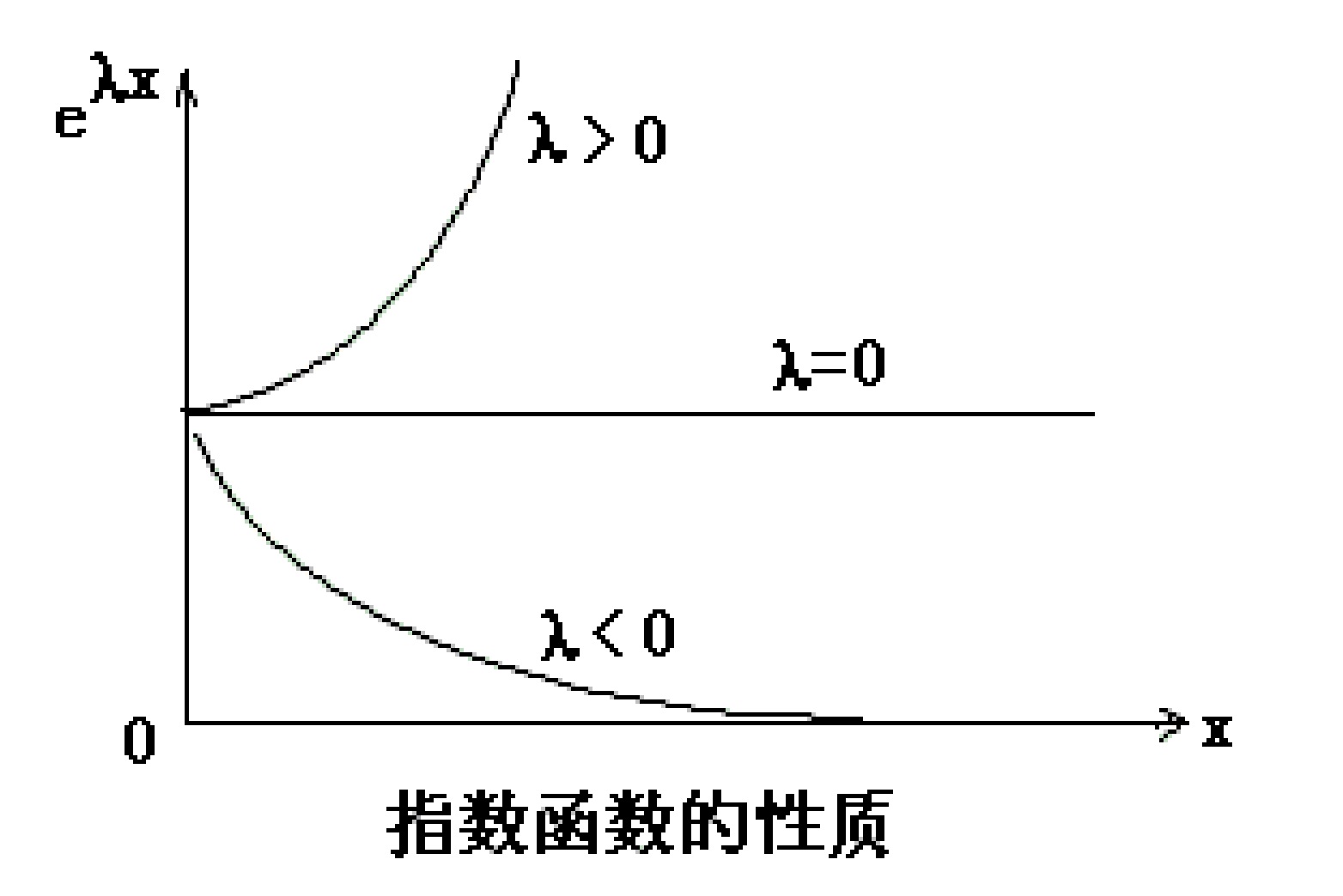
如何來判定系統穩定與否?李亞普洛夫想,可以用對重力場中兩個小球是否穩定的類似判定方法。於是,他研究當初值變化一點點時,看看系統的最終結果如何變化,並以此來作為穩定性的判據。更具體地說,我們可以將系統的最終結果x無窮表示成初始值x0的函數,用圖形畫出來。然後,系統的穩定性取決於這個函數圖形的走向:它是更接近圖(20.3)中的哪一種曲線呢?是向下指數衰減(λ小於0)?還是向上指數增長(λ大於0)?還是平直一條(λ等於0)?第一種情況被認為是穩定的,第二種情況被認為是不穩定的,而λ等於0則是臨界狀態。這兒的λ便是李亞普洛夫指數。
圖(20.3):指數函數的性質隨λ變化
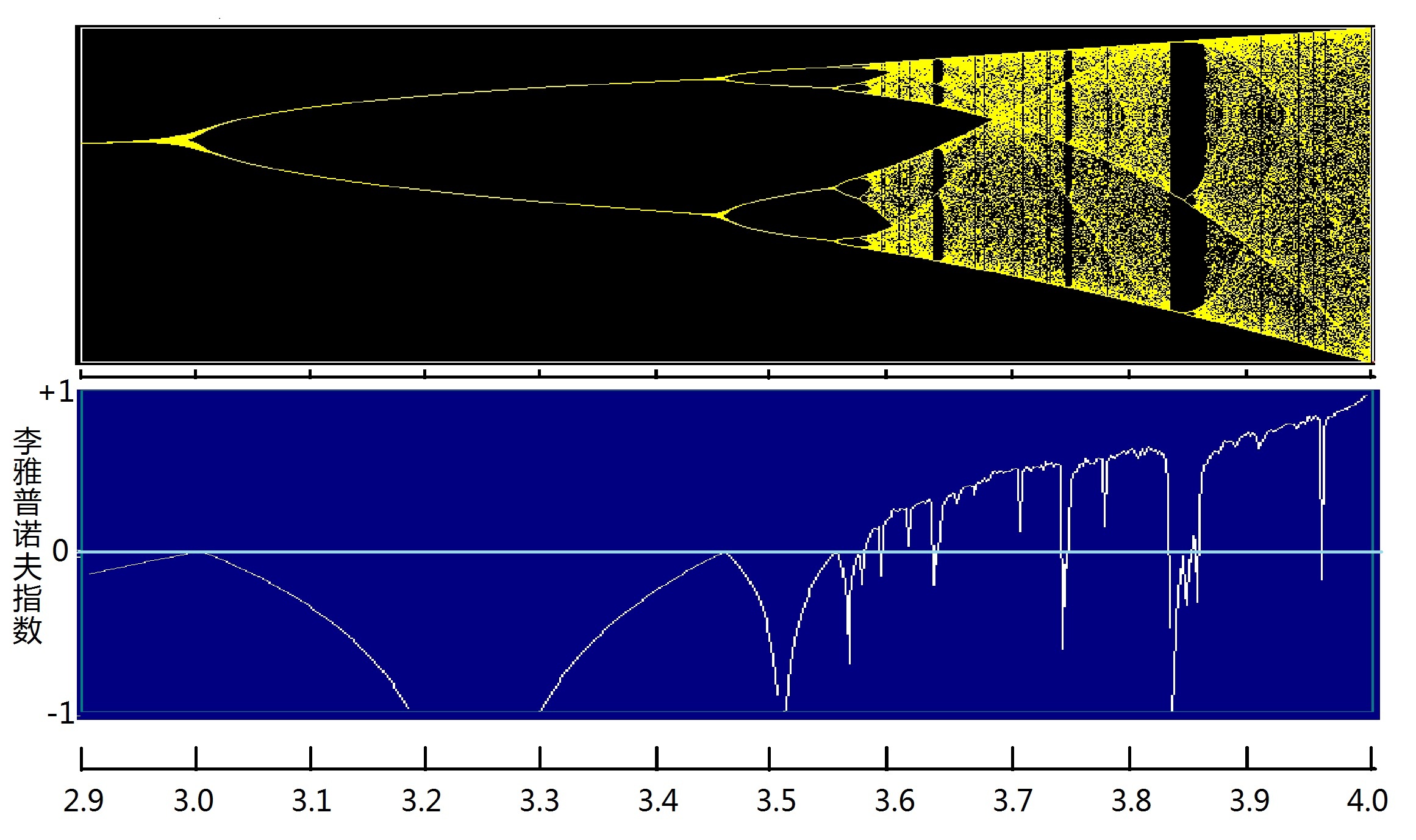
圖(20.4)顯示的便是不同k值下,邏輯斯蒂系統的李雅普諾夫指數及對應的分岔圖,從中不難看出λ的符號變化與倍周期分岔的產生及混沌魔鬼出現之間的關係:k值比較小的時候,λ小於0,系統處於穩定狀態;從k=3.0開始,λ有時等於0,出現分岔現象,系統變到多態平衡,但仍然是穩定的,大多數時候,λ小於0;從k>3.57開始,λ開始大於0,系統不穩定,過渡到混沌。有趣的是,混沌魔鬼露臉後又經常躲藏起來。在λ大於0的區間中,λ的數值還經常返回到小於0的數值。也就是說,混沌有時又變成有序,這對應於分岔圖中(黃色圖像)中的空白地帶。
圖(20.4):邏輯斯蒂系統的李雅普諾夫指數及對應的分岔情形
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | 可適合居住的行星 | |
| 2011: | 天邊的紅霞:賓州公立小學資優班 | |
| 2010: | 鷹熊戀:rondeau 請achc指正 | |
| 2010: | 日行一善,替路過同學批改“鷹熊戀(ro | |
| 2009: | 中國人的標準像 | |
| 2009: | [故事] 裸 | |
| 2008: | 遠芳:零距離接觸余秋雨 | |
| 2008: | 當你年輕的時候, 想想“老”了怎麼辦 | |
| 2007: | 張維迎的管理三板斧 | |
| 2007: | 方舟子對《我和方舟子分手決裂的前前後 | |